Introducción a Redes Neuronales Recurrentes
Contents
Introducción a Redes Neuronales Recurrentes#
Conceptos básicos
Fuente: Alvaro Montenegro
Introducción#
En la introducción a procesamiento de lenguaje natural introducimos los modelos \( n \)-gram. En tales modelos la probabilidad condicional de la palabra \( x_t \) en el paso de tiempo \( t \) solo depende de \( n-1 \) las palabras anteriores .
Si queremos incorporar el posible efecto de palabras anteriores al paso de tiempo \( t-(n-1) \) en \( x_t \), necesitamos aumentar \( n \).
Sin embargo, el número de parámetros del modelo también aumentaría exponencialmente con él, ya que necesitamos almacenar \( | \mathcal{V} |^n \) números para un conjunto de vocabulario \( \mathcal{V} \). Por lo tanto, en lugar de modelar \( P (x_t \mid x_ {t-1}, \ldots, x_{t-n + 1}) \), es preferible usar un modelo de variable latente:
en donde \( h_{t-1} \) es un estado oculto (también conocido como variable oculta) que almacena la información de la secuencia hasta el paso de tiempo \( t-1 \).
En general, el estado oculto en cualquier paso de tiempo \( t \) podría calcularse basándose tanto en la entrada actual \( x_{t} \) como en el estado oculto anterior \( h_{t-1} \):
Para una función suficientemente poderosa \( f \), el modelo de variable latente no es una aproximación. Después de todo, \( h_t \) simplemente puede almacenar todos los datos que ha observado hasta ahora. Sin embargo, potencialmente podría encarecer tanto la computación como el almacenamiento.
Recuerde que hemos hablado de capas ocultas con unidades ocultas cuando introducimos los perceptrones multicapa.
Cabe destacar que capas ocultas y estados ocultos se refieren a dos conceptos muy diferentes.
Las capas ocultas son, como se explicó, capas que están ocultas a la vista en la ruta desde la entrada hasta la salida.
Los estados ocultos son técnicamente hablando
entradasa todo lo que hacemos en un paso dado, y solo se pueden calcular observando los datos de los pasos de tiempo anteriores.
Las redes neuronales recurrentes (RNR) son redes neuronales con estados ocultos. Antes de presentar el modelo RNN, revisitemos el modelo perceptron multicapa (PMC).
Redes Neuronales con una capa oculta#
Damos un vistazo a un PMC con una sola capa oculta. Dado un mini lote de ejemplos \(\mathbf{X} \in \mathbb{R}^{d \times N}\) con tamaño de lote \(N\) y \(d\) entradas. La salida de la capa oculta, denotada por \(\mathbf{Y} \in \mathbb{R}^{h \times N}\) se calcula como
En esta ecuación tenemos que la matriz(parámetro) de pesos de la capa oculta es \(\mathbf{W}_{hd} \in \mathbb{R}^{d \times h}\), el vector sesgo (bias) de la capa oculta es \(\mathbf{b}_h \in \mathbb{R}^{h\times 1}\), \(B = [\mathbf{b}_h, \ldots, \mathbf{b}_h ]_{h \times N}\), \(h\) es el número de unidades ocultas de la capa oculta y \(g\) la función de activación de la capa oculta.
Ahora, la variable oculta \(\mathbf{Y}\) se utiliza como entrada de la capa de salida. La capa de salida está dada por
en donde \(\mathbf{Z} \in \mathbf{R}^{q \times N}\) es la variable de salida, \(\mathbf{V}_{q \times h} \in \mathbb{R}^{q \times h}\) es la matriz (parámetro) de pesos de la capa de salida, \(\mathbf{C} \in \mathbb{R}^{q \times N}\), con \(\mathbf{C} = [\mathbf{c}_q, \ldots, \mathbf{c}_q ]_{q \times N}\), \(\mathbf{c}_q \in \mathbb{R}^{q \times 1}\) el parámetro de sesgo de la capa de salida y \(f\) la función de activación de la capa de salida. Si se trata de un problema de clasificación, podemos utilizar \(\text{softmax}(\mathbf{Z})\) para calcular la distribución de probabilidad de las categorías de salida.
Esto es completamente análogo a un problema de regresión no lineal usando redes neuronales, por lo que omitimos detalles.
Baste decir que podemos elegir pares de características y etiquetas al azar y aprender (estimar) los parámetros de nuestra red a través de la diferenciación automática y el descenso de gradiente estocástico.
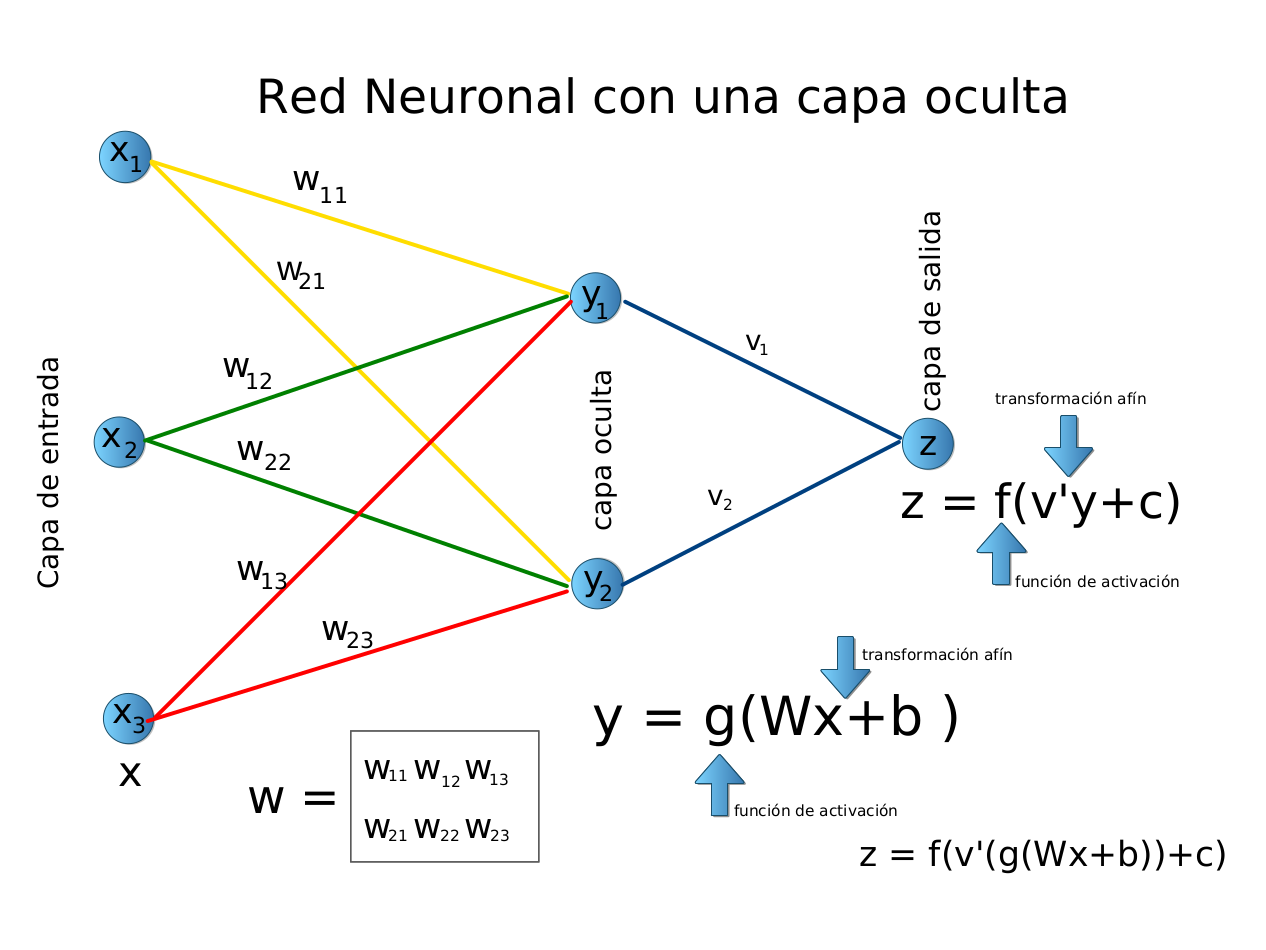
La siguiente imagen ilustra el caso cuando se tiene \(d=3\), \(h=2\), \(q=1\) y \(N=1\).
Redes Neuronales con estados ocultos#
Las cosas son completamente diferentes cuando tenemos estados ocultos. Veamos la estructura con más detalle.
Supongamos que tenemos un minilote de entradas \( \mathbf{X}^{(t)} \in \mathbb{R} ^ {d \times N} \) en el paso de tiempo \( t \). En otras palabras, para un minilote de \( N \) ejemplos de secuencia, cada columna de \( \mathbf{X}^{(t)} \) corresponde a un ejemplo en el paso de tiempo \( t \) de la secuencia.
En adelante \(\mathbf{H}^{(t)} \in \mathbb{R}^{h \times N} \) denotará la variable oculta en el paso de tiempo \( t \).
A diferencia del PMC, aquí guardamos la variable oculta \( \mathbf {H}^{(t-1)} \) del paso de tiempo anterior e introducimos una nueva matriz (parámetro) de peso \( \mathbf{W}_{hh} \in \mathbb{R }^{h \times h}\) para transformar la variable oculta del paso de tiempo anterior en el paso de tiempo actual. En adelante \( \mathbf{W}_{hd} \in \mathbb{R }^{h \times d}\) denotará a la matriz de pesos aplicada a la siguiente nueva entrada \( \mathbf {X}^{(t)} \)
Cálculo del estado oculto#
Específicamente, el cálculo de la variable oculta del paso de tiempo actual está determinado por la entrada del paso de tiempo actual junto con la variable oculta del paso de tiempo anterior:
En donde \(\mathbf{b}_h \in \mathbb{R}^{h\times 1}\), \(B = [\mathbf{b}_h, \ldots, \mathbf{b}_h ]_{h \times N}\)
En comparación con la ecuación de la salida de la capa oculta arriba, esta ecuación agrega el término \( \mathbf {W}_{hh}\mathbf{H}^{(t-1)} \).
De la relación entre las variables ocultas \( \mathbf{H}^{(t)} \) y \( \mathbf{H}^{(t-1)}\) de pasos de tiempo adyacentes, se desprende que estas variables capturan y retienen la información histórica de la secuencia hasta su paso de tiempo actual.
La variable oculta se denomina estado oculto. Dado que el estado oculto usa la misma definición del paso de tiempo anterior en el paso de tiempo actual, el cálculo de \( \mathbf {H}^{(t)}\) es recurrente. Por esta razón las redes neuronales con estados ocultos basados en cálculos recurrentes se denominan redes neuronales recurrentes.
Capas que ejecutan el cálculo de esta última ecuación se llaman capas recurrentes.
Hay muchas formas diferentes de construir RNR. Las RNR con un estado oculto definido arriba son muy comunes.
Cálculo de la salida en la capa de salida para el tiempo \(t\)#
Para el paso de tiempo \( t \), la salida de la capa de salida es similar al cálculo en el PMC:
Los parámetros de la RNR incluyen los pesos \( \mathbf{W}_{dh} \in \mathbb{R}^{d \times h}, \mathbf{W}_{hh} \in \mathbb{R}^{h \times q}\) y el sesgo \( \mathbf{b}_h \in \mathbb{R}^{1 \times h} \) de la capa oculta, junto con los pesos \( \mathbf {W} _ {hq} \in \mathbb {R} ^ {h \times q} \) y el sesgo \( \mathbf{b}_q \in \mathbb{R}^{1 \times q} \) de la capa de salida.
Vale la pena mencionar que incluso en diferentes pasos de tiempo, Los RNR siempre usan estos parámetros de modelo. Por tanto, el costo de parametrización de un RNR no crece a medida que aumenta el número de pasos de tiempo.
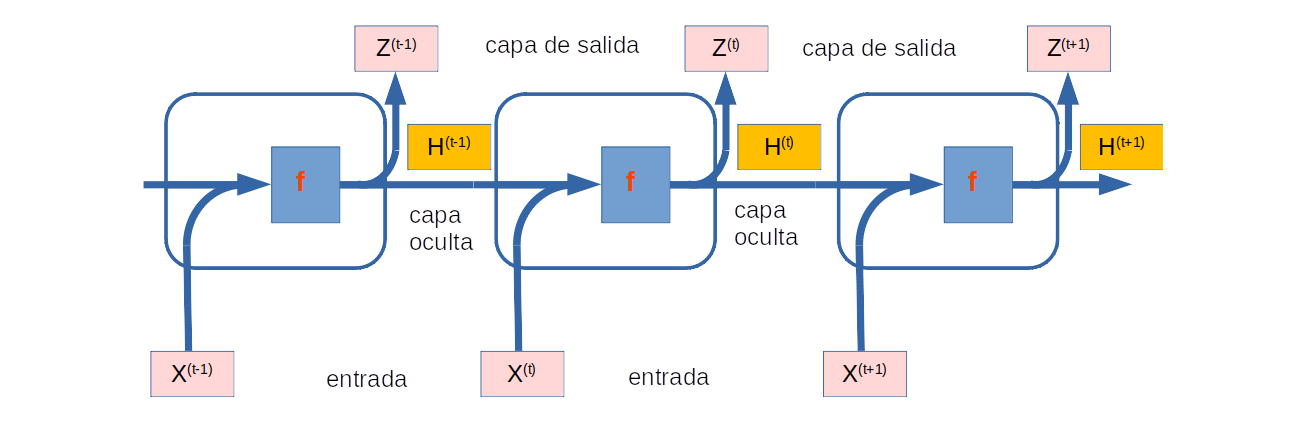
La siguiente figura ilustra la lógica computacional de un RNR en tres pasos de tiempo adyacentes. En cualquier momento paso \( t \), el cálculo del estado oculto se puede entender como:
concatenando la entrada \( \mathbf {X}^{(t)} \) en el paso de tiempo actual \( t \) y el estado oculto \( \mathbf {H}^{(t-1)} \) en el paso de tiempo anterior \( t-1 \);
pasar el resultado de la concatenación a una capa completamente conectada con función de activación \( f \).
Fuente: Alvaro Montenegro
Redes Neuronales basados en Modelos de lenguaje caracter-etiqueta#
Recuerde que para el modelado de idiomas nuestro objetivo es predecir el siguiente token basado en los tokens actuales y anteriores, Así cambiamos la secuencia original por un token. como las etiquetas. Bengio et al. fueron los primeros en proponer usar una red neuronal para el modelado de idiomas.
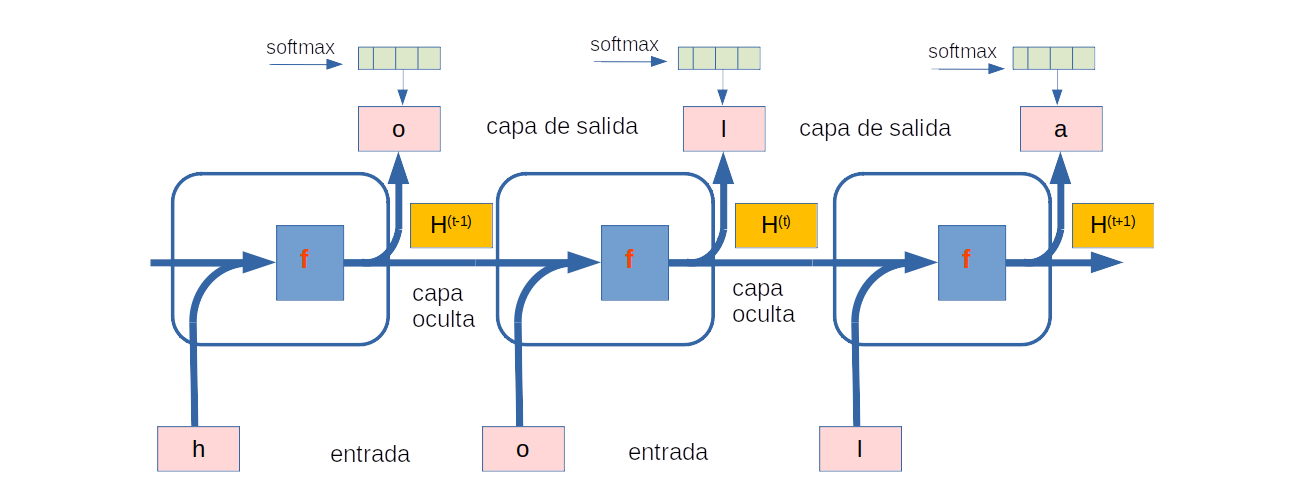
A continuación ilustramos cómo se pueden usar RNN para predecier el siguiente caracter en un modelo de idioma basado en caracteres. Dejaremos que el tamaño del minilote sea uno, y la secuencia del texto sea «machine».
Para simplificar, tokenizamos el texto en caracteres en lugar de las palabras y consideramos un modelo de lenguaje de nivel de carácter.
La siguiente figura muestra cómo predecir el siguiente carácter en función de los caracteres actuales y anteriores a través de una RNR para el modelado de lenguaje de nivel de carácter.

Fuente: Alvaro Montenegro
Durante el proceso de entrenamiento,
Ejecuamos una operación SoftMax en la salida de la capa de salida para cada paso de tiempo, y luego usamos la pérdida entropía cruzada para calcular el error entre la salida del modelo y la etiqueta.
Debido al cálculo recurrente del estado oculto en la capa oculta, la salida del tiempo en el paso 3 en la figura, es \( \mathbf{Z} _3\), y está determinado por la secuencia de texto «h», «o», y «l», . Dado que el siguiente carácter de la secuencia en los datos de entrenamiento es «a», la pérdida en el tiempo o paso 3 dependerá de la distribución de probabilidad del siguiente carácter generado en función de la secuencia de características «h», «o», «l» y la etiqueta «a» de este paso de tiempo.
En la práctica, cada token está representado por un vector \( d \)-dimensional, y usamos un tamaño de lote \( n> 1 \). Por lo tanto, la entrada \( \mathbf{X}^{(t)} \) en el momento \( t \) será una matriz de \( d \times N \), que es idéntica a la que discutimos antes.
Perplexity#
Por último, analicemos cómo medir la calidad del modelo de lenguaje, que se utilizará para evaluar nuestros modelos basados en RNR en las secciones siguientes.
Una forma de evaluar la calidad del modelo de lenguaje es calcular lo sorprendente que resulta el texto. Un buen modelo de lenguaje puede predecir con tokens de alta precisión como revisamos a continuación. Considere las siguientes continuaciones de la frase «Está lloviendo», según lo propuesto por diferentes modelos de lenguaje:
«Está lloviendo afuera»
«Está lloviendo banano»
«Está lloviendo piouw; kcj pwepoiut»
En términos de calidad, el ejemplo 1 es claramente el mejor. Las palabras son sensatas y lógicamente coherentes. Si bien es posible que no refleje con precisión qué palabra sigue semánticamente («en San Francisco» y «en invierno» habrían sido extensiones perfectamente razonables), el modelo es capaz de capturar qué tipo de palabra sigue.
El ejemplo 2 es considerablemente peor al producir una extensión sin sentido. No obstante, al menos el modelo ha aprendido a deletrear palabras y cierto grado de correlación entre las palabras. Por último, el ejemplo 3 indica un modelo mal entrenado que no se ajusta a los datos correctamente.
Podríamos medir la calidad del modelo calculando la probabilidad de la secuencia. Desafortunadamente, este es un número difícil de entender y de comparar. Después de todo, es mucho más probable que ocurran secuencias más cortas que las más largas, de ahí la evaluación del modelo de la obra magna de Tolstoi La guerra y paz producirá inevitablemente una probabilidad mucho menor que, por ejemplo, en la novela de Saint-Exupery El Principito. Lo que falta es el equivalente a un promedio.
Como sabemos de antes, La entropía mide el grado de sorpresa de un resultado en una distribución discreta y entropía cruzada mide el grado de sorpesa de un resultado de una distribución en relación con una distribución de referencia.
Si queremos comprimir texto, podemos preguntar sobre el siguiente token dado el conjunto actual de tokens. Un mejor modelo de lenguaje debería permitirnos predecir el próximo token con mayor precisión. Por lo tanto, debería permitirnos gastar menos bits en comprimir la secuencia.
Entonces podemos medirlo por la pérdida de la entropía cruzada promediada sobre todos los \( n \) tokens de una secuencia:
donde \( P \) viene dado por un modelo de lenguaje y \( x_t \) es el token real observado en el paso de tiempo \( t \) de la secuencia. Observe que para este cálculo se usa la entropía cruzada. La distribución de referencia es la codificación one-hot de la etiqueta correspondiente, en cada salida. Además \(P(x_t \mid x_{t-1}, \ldots, x_1)\) se calcula a partir de \(\text{Softmax}(h_t)\).
Esto hace que el rendimiento en documentos de diferentes longitudes sea comparable. Por razones históricas, los científicos en el procesamiento del lenguaje natural prefieren usar una cantidad llamada perplexity. En pocas palabras, es el exponencial de la anterior ecuacion:
La perplejidad (perplexity) puede entenderse mejor como la media armónica del número de opciones reales que tenemos al decidir qué token elegir a continuación.
Veamos algunos casos:
En el mejor de los casos, el modelo siempre estima perfectamente la probabilidad del token de etiqueta como 1. En este caso, la perplejidad del modelo es 1.
En el peor de los casos, el modelo siempre predice la probabilidad del token de etiqueta como 0. En esta situación, la perplejidad es infinito positivo.
En la línea de base, el modelo predice una distribución uniforme sobre todos los tokens disponibles del vocabulario. En este caso, la perplejidad (perplexity) es igual al número de tokens únicos del vocabulario. De hecho, si tuviéramos que almacenar la secuencia sin ninguna compresión, esto sería lo mejor que podríamos hacer para codificarla. Por lo tanto, esto proporciona un límite superior no trivial que cualquier modelo útil debe superar.
Resumen#
Una red neuronal que utiliza computación recurrente para estados ocultos se denomina red neuronal recurrente (RNN).
El estado oculto de un RNN puede capturar información histórica de la secuencia hasta el paso de tiempo actual.
El número de parámetros del modelo RNN no aumenta a medida que aumenta el número de pasos de tiempo.
Podemos crear modelos de lenguaje a nivel de personaje usando un RNN.
Podemos utilizar la perplejidad para evaluar la calidad de los modelos lingüísticos.
Ejercicios#
Si usamos un RNN para predecir el siguiente carácter en una secuencia de texto, ¿cuál es la dimensión requerida para cualquier resultado?
¿Por qué los RNN pueden expresar la probabilidad condicional de un token en algún paso de tiempo basándose en todos los tokens anteriores en la secuencia de texto?
¿Qué le sucede al gradiente si se propaga hacia atrás a través de una secuencia larga?
¿Cuáles son algunos de los problemas asociados con el modelo de lenguaje descrito en esta sección?


