Tensores y distribuciones de probabilidad
Contents
Tensores y distribuciones de probabilidad#
Introducción#
En esta lección estudiaremos una red neuronal artifical de clasificación.
Al finalizar vamos a concluir que lo que hace la red neuronal es transformar un tensor en una distribución de probabilidad.
Red Neuronal de clasificación#
La siguiente imagen ilustra una red neural artificial que se entrenará para clasificar objetos en tres clases.
Fuente: Journal of Low Power Electronics and Applications
La red tiene tres capas:
Capa de entrada
Una capa oculta
Una capa de salida
Por fuera de la red, la salida es transformada en una probabilidad
Una red neuronal de clasificación es una máquina (modelo) que es entrenada para clasificar objetos en distintas clases.
Modo Inferencia#
Recuerde que la red neuronal artifical es una función matemática, no lineal, que toma una entrada y produce una salida.
Una vez la red es entrenada (ver modo entrenamiento abajo), la red hace el siguiente trabajo.
Recibe un tensor, que por ejemplo representa una imágen, las características de una flor (iris, …) y lo transforma (o proyecta) de manera no lineal en un espacio, representado por la capa oculta. La siguiente imagen puede darle una idea de lo que ocurre.
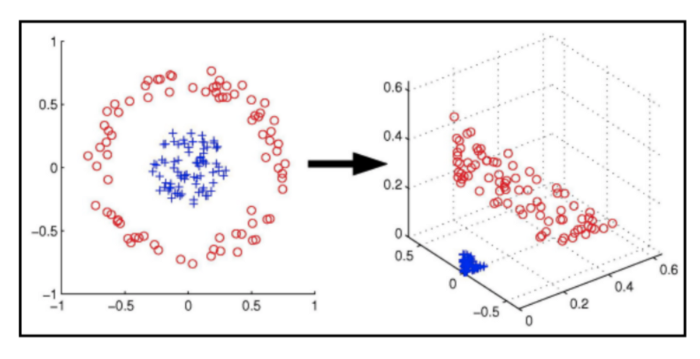
En este nuevo espacio, el tensor es identificado con unas nuevas coordenadas. Aquí puede imaginarse que se encuentra en la capa oculta (hidden).
Ahora, dependiendo del número de categorias o clases en el problema, digamos tres, hace una transformación hacia un nuevo espacio que tiene una dimensión igual al número de categorías. Esta transformación ubica al tensor en un espacio que podemos denominar de pre-probabilidad.
De acuerdo a los patrones que haya recibido la red en el modo entrenamiento, el espacio de salida es teóricamente construido de tal manera que se tiene una partición como se muestra en el siguiente gráfico de ejemplo.
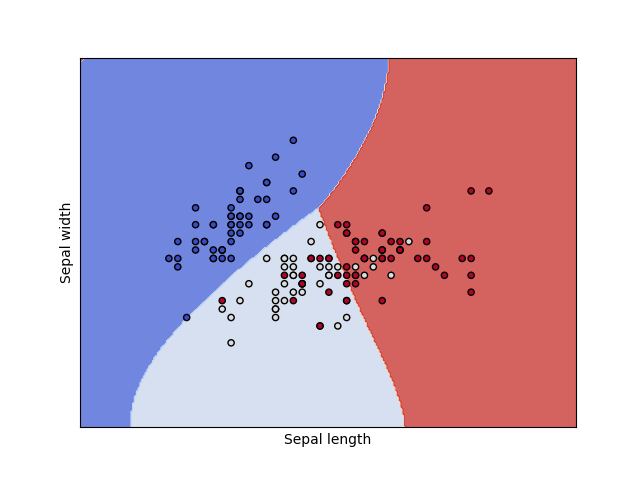
Fuente: Classification with Support Vector Machines
Cada componente corresponde a una posición relacionada con cada una de las áreas mostradas en el gráfico. El punto de intersección puede pensarse como un cero \((0,0,0)\). En la medida en que un objeto representado aquí se aleja en dirección de un color, la correspondiente coordenada crece.
Entonces observe que aquellos objetos que queden cerca a algún margen quedaran con valores similares en las respectivas componentes. Eso explica porque la red no clasifica 100% bien.
Modo entrenamiento#
En el modo entrenamiento, entran muchos patrones y el objetivo es determinar los pesos sinápticos que permitiran en el modo inferencia proyectar un tensor de entrada en un punto del espacio de salida.
Tensores como distribuciones de probabilidad#
Función softmax#
Dada una posición en el espacio de salida, digamos \(z=(z_1,z_2,z_3)\), la función softmax se define se manera sencilla como:
Por ejemplo,
si \(z=(0,0,0)\), entonces \(p=(0.333,0.333, 0.333)\).
si \(z =(6,1,2)\), entonces \(p = (0.976,0.007 ,0.018)\)
si \(z=(-1,6,3)\), entonces \(p = (0.001,0.952 ,0.046)\)
si \(z= (2.5,2.2,2.6)\), entonces \(p = (0.351, 0.26 , 0.388)\)
La última parte del trabajo es una trasformación matemática por fuera de la red, que convierte las coordenadas del espacio de salida (espacio de pre-probabilidad) en una distribución de probabilidad.
Es decir, cada posible tensor queda finalmente representado como una distribución de probabilidad.
El siguiente gráfico corresponde a la distribución de un posible tensor de entrada.
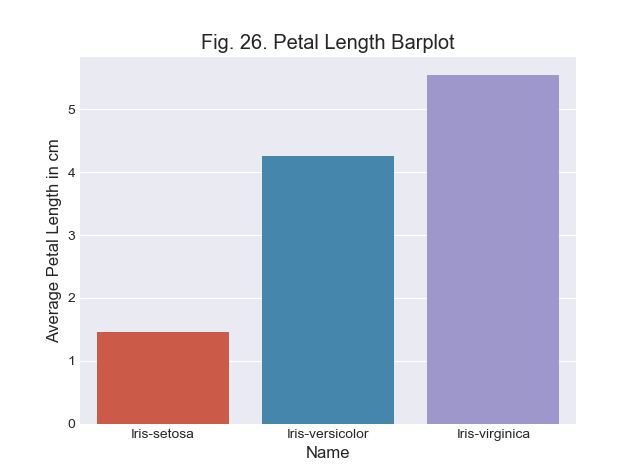
Fuente: Programming and Scripting - Dermot Kelleher
Esta representación de los tensores en forma de distribución de probabilidad asociada a las categorías es el insumo para la clasificación.


