Variables Aleatorias

Conceptos básicos

Fuente: Alvaro Montenegro

Introducción

En esta sección se introducen conceptos básicos de variables aleatorias, funciones de probabilidad y distribución acumulada.

Ejemplo de los dados

Recordemos el ejercicio de la sección anterior Probabilidad. La imagen muestra dos dados de seis caras de distinto color.

Dos datos de seis caras

Fuente: pixabay

*Como ya se sabe del ejercicio hay 36 posibles resultados. Es decir el espacio muestral \(\mathcal{M}\) tiene 36 elementos y \(2^{36}\) eventos.

Supongamos que \((x,y)\) es un elemento de \(\mathcal{M}\). Observe que \((x,y)\) es en realidad una pareja de números. Por ejemplo \((3,4)\). Definamos ahora la siguiente función:

\[ f(x,y) = x+y, \]

es decir la función \(f\) simplemente calcula la suma de los dos números. Como el espacio muestral tiene 36 elementos, entonces hay 36 posibles resultados, aunque no todos son diferentes.

La función \(f\) se llama una variable aleatoria. Veamos algunos posibles valores que puede tomar la función:

\[\begin{split} \begin{align*} f(1,1) & = 2\\ f(3,2) & = 5\\ f(4,3) & = 7\\ f(3,4) & = 7\\ f(6,5) & = 11 \end{align*} \end{split}\]

Variable aleatoria

Dado un espacio muestral \(\mathcal{M}\), es una función que asigna a los elementos del espacio muestral un número real.

En el espacio muestral de los dos dados de seis lados, se pueden definir muchas variables aleatorias. Considere por ejemplo la variable aleatoria definida por: $\(g(x,y) = x\times y\)$

Ejercicio

Considere el ejemplo del espacio muestral de los dos dados de seis caras, no cargados.

1. Construya la tabla completa de los posibles resultados de de las funcioens \(f\) y \(g\).

2. Proponga otra variable aleatoria definida sobre el espacio muestral \(\mathcal{M}\).

Ayuda: Use Python. Construya primero la tabla que representa el espacio muestral, en un tensor \(36\times 2\). En otro tensor construya los respectivos valores de la función.

# libreria numérica
import numpy as np

# espacio muestral
M = np.zeros((36,2))
k = 0
for i in range(1,7):
    for j in range(1,7):
        M[k,] = (i,j)
        k+=1

        
# calcula la variable aleatoria f: f(x,y)=x+y        
f = np.zeros(36)
for k in range(36):
    f[k] = M[k,0] + M[k,1]

    
# presenta los resultados
for k in range(36):
    print('f(',M[k,0],',',M[k,1],') =', f[k])

f( 1.0 , 1.0 ) = 2.0
f( 1.0 , 2.0 ) = 3.0
f( 1.0 , 3.0 ) = 4.0
f( 1.0 , 4.0 ) = 5.0
f( 1.0 , 5.0 ) = 6.0
f( 1.0 , 6.0 ) = 7.0
f( 2.0 , 1.0 ) = 3.0
f( 2.0 , 2.0 ) = 4.0
f( 2.0 , 3.0 ) = 5.0
f( 2.0 , 4.0 ) = 6.0
f( 2.0 , 5.0 ) = 7.0
f( 2.0 , 6.0 ) = 8.0
f( 3.0 , 1.0 ) = 4.0
f( 3.0 , 2.0 ) = 5.0
f( 3.0 , 3.0 ) = 6.0
f( 3.0 , 4.0 ) = 7.0
f( 3.0 , 5.0 ) = 8.0
f( 3.0 , 6.0 ) = 9.0
f( 4.0 , 1.0 ) = 5.0
f( 4.0 , 2.0 ) = 6.0
f( 4.0 , 3.0 ) = 7.0
f( 4.0 , 4.0 ) = 8.0
f( 4.0 , 5.0 ) = 9.0
f( 4.0 , 6.0 ) = 10.0
f( 5.0 , 1.0 ) = 6.0
f( 5.0 , 2.0 ) = 7.0
f( 5.0 , 3.0 ) = 8.0
f( 5.0 , 4.0 ) = 9.0
f( 5.0 , 5.0 ) = 10.0
f( 5.0 , 6.0 ) = 11.0
f( 6.0 , 1.0 ) = 7.0
f( 6.0 , 2.0 ) = 8.0
f( 6.0 , 3.0 ) = 9.0
f( 6.0 , 4.0 ) = 10.0
f( 6.0 , 5.0 ) = 11.0
f( 6.0 , 6.0 ) = 12.0

Cálculo de frecuencias

Observe que en el ejemplo anterior, la variable aleatoria toma once(11) posibles valores diferentes:

\[f=\{ 2,3,4,5,6,7,8,9,10,11,12\}\]

Entonces tenemos lo siguiente: 36 posibles valores, pero solamente 11 diferentes. El siguiente fragmento de código muestra como obtener los posibles valores diferentes que toma la variable aleatoria \(f\).

print(np.unique(f)) 

[ 2.  3.  4.  5.  6.  7.  8.  9. 10. 11. 12.]

Función Python para calcular una tabla de frecuencias

La siguiente función muestra un camino de como calcular la tabla de frecuencias de un conjunto de datos, puestos en una lista de Python. No es la única forma. Investigue otras formas de hacerlo.

# Función Python para contar los elementos la fecuencia
# de los elementos de una lista, usando un diccionario
  
def CountFrequency(my_list): 
  
    # Creando un diccionario vacío  
    freq = {} 
    for item in my_list: 
        if (item in freq): 
            freq[item] += 1
        else: 
            freq[item] = 1
    return freq           
 

Asegúrese de entender completamente el código. Vamos a probar la función con dos ejemplos. Primero calculamos la frecuencia de los valores de la variable aleatoria \(f\).

frec = CountFrequency(f)   

for key, value in frec.items():
    print ("% d : % d"%(key, value)) 

 2 :  1
 3 :  2
 4 :  3
 5 :  4
 6 :  5
 7 :  6
 8 :  5
 9 :  4
 10 :  3
 11 :  2
 12 :  1

Podemos manipular directamente los valores del diccionario. Por ejemplo para calcular la frecuencia de 7, que ya sabemos es 6, se escribe:

frec[7]

6

En un segundo ejemplo, consideremos el conjunto \( W= \{A,B,B,C,A,A \}\)

W = ['A','B','B','C','A','A']
frec = CountFrequency(W)   
frec['B']

2

Función de Probabilidad de una variable numérica discreta

Ahora que hemos aprendido a calcular tablas de frecuencias de conjuntos de datos organizados en una lista, vamos a introducir el concepto clave de función de probabilidad. En esta sección consideramos variables aleatorias numéricas discretas como la función \(f\) asociada al espacio muestral del lanzamiento de dos dados no cargados. En la siguiente sección consideramos variables categóricas y en otra lección consideramos variables continuas.

Como observamos antes, la variable aleatoria \(f\) es discreta (particularmente es finita), debido a que toma únicamente 11 posibles valores numéricos. Por otro lado sabemos que el resultado del experimento de lanzar los dados puede arrojar 36 posibles resultados. La función de probabilidad de la variable aleatoria f, que notaremos \(p_f\) se define como la probabilidad de obtener cada posible valor de f.

Entonces como vimos arriba tenemos que la función de probabilidad de la variable aleatoria \(f\) está definida por extensión de la siguiente forma:

\[\begin{split} \begin{align*} p_f[2] & = 1/36\\ p_f[3] & = 2/36\\ p_f[4] & = 3/36\\ p_f[5] & = 4/36\\ p_f[6] & = 5/36\\ p_f[7] & = 6/36\\ p_f[8] & = 5/36\\ p_f[9] & = 4/36\\ p_f[10] & = 3/36\\ p_f[11] & = 2/36\\ p_f[12] & = 1/36 \end{align*} \end{split}\]

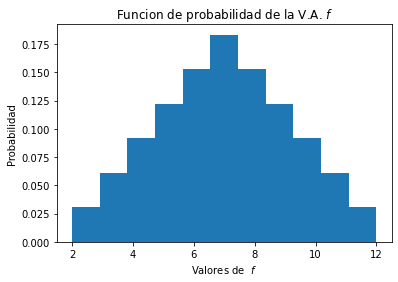
Podemos obtener una imagen de la función, utilizando un histograma. Un histograma es un gráfico de una función de probabilidad de una variable numérica. El siguiente código Python muestra como construir un histograma de la variable aleatoria f.

import matplotlib.pyplot as plt
plt.hist(f, bins=11,density=True)
plt.title('Funcion de probabilidad de la V.A. $f$')
plt.xlabel('Valores de  $f$')
plt.ylabel('Probabilidad')
plt.show()

Cálculo de algunas probabilidades

Dado que la variable aleatoria \(f\) es numérica, podemos calcular la probabilidad de diferentes eventos del espacio muestral, basados en el valor de \(f\). Veamos algunos ejemplos.

\[\begin{split} \begin{align*} \text{Prob}[f \text{ es par }] &= 18/36\\ \text{Prob}[f\le 6] &= 15/36\\ \text{Prob}[f> 10] &= 3/36\\ \text{Prob}[f \text{ es par }|f<5] &= 4/6 \end{align*} \end{split}\]

Por favor verifique estos resultados.

Interpretación de la función de probabilidad

Supongamos que el experimento de lanzar se repite muchas veces. Digamos 100 veces. Como la probabilidad de obtener digamos \(f=7\) es \(6/36\), entonces lo que se espera que ocurra es que en los 100 lanzamientos se obtenga un valor cercano a:

\[ \text{Número de veces que se espera que ocurra }\{f=7\} = \tfrac{6}{36}\times 100 \approx 17. \]

Por supuesto, no necesariamente el resultado será 17. Pero si un número cercano. Por ejemplo no esperamos que no ocurra ninguna vez o que ocurra todas las veces el resultado \(\{f=7\}\).

Ejemplos de variables numéricas discretas

Variable de Bernoulli (Distribución de Bernoulli)

Una variable aleatoria \(f\) es Bernoulli, si solamente toma dos posibles valores, los cuales por convención son \(\{0,1\}\). Es común llamar al resultado 1 como éxito y a 0 como fallo. Observe que en este caso se tiene que la función de probabilidad es dada por:

\[\begin{split} \begin{align*} p_f[1] &= \pi\\ p_f[0] &= 1-\pi, \end{align*} \end{split}\]

en donde \(\pi = \text{Prob}[f=1]\). En este caso, se puede escribir la función en una forma más compacta como:

\[ p_f[x] = \pi^{x}(1-\pi)^{1-x}, \quad x=0,1. \]

Asegúrese de entender la fórmula anterior.

Un ejemplo es el siguiente. En el experimento del lanzamiento dados no cargados, definimos la variable aleatoria \(g\) como sigue:

\[\begin{split} g = \begin{cases} &1, \text{ si la suma de los dos dados es par} \\ &0, \text{ si la suma de los dos dados es impar} \end{cases} \end{split}\]

Verifique que en este caso \(\pi =18/36=1/2\).

Variable Binomial (Distribución Binomial)

Consideremos la variable aleatoria \(g\) definida arriba. Pero ahora vamos a considerar que hacemos el experimento digamos \(N=3\) veces y contamos el número de veces en que \(g=1\). Por otro lado vamos a suponer que que hay un sesgo en el experimento (una especie de dados cargados y se verifica que \(\text{Prob}[g=1] = 0.6\). Por lo tanto se tiene que \(\text{Prob}[g=0] = 0.4\).

Entonces obtenemos una variable aleatoria que llamaremos \(q\) y diremos que \(q\) es una variable Binomial. La función de probabilidad de la variable aleatoria \(q\) es dada por extensión como sigue. La variable \(q\) toma 4 posibles valores, \(q = \{0,1,2,3\}\)

Veamos como calcular las probabilidades de los valores de \(q\). La siguiente tabla muestra como calcular tales probabilidades.

Valor	Experimentos	probabilidad cada experimento	probabilidad para este valor de f	total
0	000	\(0.4\times 0.4 \times 0.4\)	0.064	0.064
1	100	\(0.6\times 0.4 \times 0.4\)	0.096
1	010	\(0.4 \times 0.6\times 0.4\)	0.096
1	001	\(0.4 \times 0.4\times 0.6\)	0.096	0.288
2	110	\(0.6\times 0.6 \times 0.4\)	0.144
2	011	\(0.4 \times 0.6\times 0.6\)	0.144
2	101	\(0.6 \times 0.4 \times 0.6\)	0.144	0.432
3	111	\(0.6 \times 0.6\times 0.6\)	0.216	0.216

Entonces se tienen que:

\[\begin{split} \begin{align*} p_q[0] & = 0.064 \\ p_q[1] & = 0.288\\ p_q[2] & = 0.432\\ p_q[3] & = 0.216 \end{align*} \end{split}\]

Ejercicio

Verifique los cálculos de la tabla anterior y asegúrese de entender completamente.

El siguiente código muestra como calcular la función de probabilidad de la variable Binomial \(q\) y como obtener un gráfico de la función.

import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt

N, p  = 3, 0.6
p_q = np.zeros(4)

for k in range(4):
    p_q[k] = binom.pmf(k,N,p)

print('p_q=',p_q)
label = ['0','1','2','3']
plt.bar(label, p_q, color = 'orange', edgecolor='blue',width=1)
plt.title('Funcion de probabilidad distribución $Binomial(3,0.6)$')
plt.xlabel('Valores de  de la variable aleatoria')
plt.ylabel('Probabilidad')
plt.show()

p_q= [0.064 0.288 0.432 0.216]

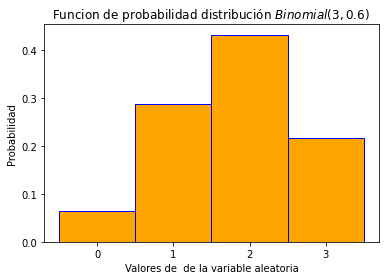
Note que la función de probabilidad de Bernoulli es un caso especial de la Binomial con \(N=1\).

Existe una formula general para la función de probabilidad de una variable Binomial. Si se supone que se hacen \(N\) experimentos de Bernoulli realizados de manera independientes con la misma probabilidad de éxito (obtener 1), y se anota el número de unos (éxitos) obtenidos, entonces la probabilidad de obtener \(k\) exitos es dada por:

\[ p_{bin}[k] = \binom{N}{k}\pi^k(1-\pi)^{N-k}, \]

en donde \(\binom{N}{k}\) es el símbolo combinatorio y \(\pi\) es la probabilidad de éxito de cada experimento de Bernoulli.

Nota

Recuerde que el combinatorio \(\binom{N}{k}\) es el número de grupos diferentes de tamaño k que se pueden formar teniendo N elementos. Consulte cualquier libro de probabilidad para los detalles matemáticos.

Variable Poisson (Distribución de Poisson)

Esta distribución es utilizada en problemas de conteo. Por ejemplo el número de bacterias por unidad de área o volumen encontradas en un cultivo microbiológico.

Una variable Poisson puede tomar teóricamente valores enteros entre cero e infinito. La función de probabilidad en este caso está dada por:

\[ p_{poi}[k] = \frac{e^{\lambda}\lambda^k}{k!},\quad k=0,1, \ldots \]

El valor \(\lambda\) se interpreta como la cantidad promedio de elementos encontrados por unidad de área, volumen, etc.

Ejercicio

1. Revise en cualquier libro de probabilidad y estadística ejemplos de aplicación de la distribución de Poisson.

2. Investigue como calcular probabilidades de la distribución de Poisson con scipy de Python. Suponga que para algún caso \(\lambda = 5.3\). Calcule las probabilidades para \( k=0,1,\ldots, 20\). Haga un gráfico de la función de probabilidad con esos datos (obviamente es una aproximación de la función completa).

3. Haga sus comentarios.

#Escriba su solución aquí

Variable categóricas

En esta sección vamos a suponer que la variable aleatoria no asigna valores numéricos a los elementos del espacio muestral. En lugar de eso, asigna etiquetas. Usualmente se dice que en este caso la variable es en realidad un objeto aleatorio. No haremos esa distinción en este desarrollo, pero sí seremos cuidadosos en tener en cuenta que la variable no es numérica.

Por facilidad usaremos de nuevo el ejemplo de los dados no cargados. Definimos la siguiente variable aleatoria que llamaremos \(X\). Para este ejercicio vamos a distinguir el color de los dados. Entonces en la pareja \((x,y)\), \(x\) corresponde al valor del dado rojo. Adicionalmente \(y\) representa el valor del dado azul. Entonces:

\[\begin{split} X((x,y)) = \begin{cases} &R, \text{ si } x>y\\ &A, \text{ si } x<y\\ &B, \text{ si } x=y\\ \end{cases} \end{split}\]

Observe que en realidad el color del dado es indiferente para la definición de la variable aleatoria.

Entonces, la función de probabilidad en este caso es dada por:

\[\begin{split} \begin{align*} p_X[R] &= \tfrac{15}{36}\\ p_X[A] &= \tfrac{15}{36}\\ p_X[B] &= \tfrac{6}{36}\\ \end{align*} \end{split}\]

Aún podemos hacer un gráfico de la función de probabilidad \(p_X\) como sigue.

import numpy as np
import matplotlib.pyplot as plt

p_X = np.array([15/36,15/36, 6/36])
label = ['R','A','B']

plt.bar(label,p_X, color = 'red', edgecolor='black',width=1)
plt.title('Funcion de probabilidad  $p_X$')
plt.xlabel('Etiquetas de  $p_X$')
plt.ylabel('Probabilidad')
plt.show()

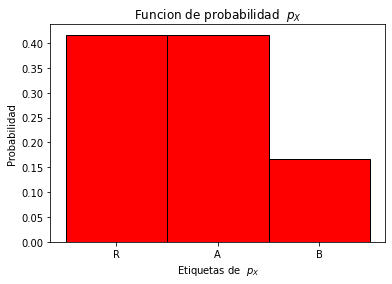
Obviamente en este caso no hay cantidades numéricas, por lo que el gráfico puede obtenerse de distintas formas, cambiando el orden de la etiquetas. Sin embargo, aún podemos hacer algunos cálculos de probabilidad.

Por ejemplo, la probabilidad de obtener R o A es dada por \(30/36\).

Esperanza Matemática de una variable aleatoria numérica

La esperanza matemática de una variable aleatoria numérica discreta es el promedio ponderado de todos sus posibles valores. La ponderación como se puede sospechar es dada por la función de probabilidad de la variable.

La definición se basa en el hecho que la función de probabilidad de la variable aleatoria representa la frecuencia relativa teórica de cada resultado particular.

Se tiene que si \(X=\{x_1,x_2,\ldots \}\) es el conjunto de valores de la variable aleatoria \(X\) y si la función de probabilidad de \(X\) es dada por \(p_X =\{p_1, p_2,\ldots \}\), en donde \(p_X[x_i] = p_i\), entonces la esperanza matemática de \(X\) se denota por \(\mathbb{E}[X]\) y es dada por:

\[ \mathbb{E}[X] = p_1x_1 + p_2x_2 +\ldots = \sum_{i} p_ix_i \]

Ejemplo

En el ejemplo de los dados se tiene que:

\[ \mathbb{E}[f] = \tfrac{1}{36}[2\times 1 + 3\times 2 + 4\times 3 + 5 \times 4 + 6\times 5 + 7\times 6 +8\times 5 + 9\times 4 + 10 \times 3 + 11 \times 2 + 12 \times 1 ] = 7. \]

Puede también calcular la esperanza de \(f\) con numpy como sigue.

np.mean(f)

7.0

Esperanza de la distribución Binomial

En el caso del ejemplo Binomial de la moneda cargada que se lanza tres veces tenemos que

\[ \mathbb{E}[f] = 0\times 0.064 + 1 \times 0.288 + 2 \times 0.432 + 3 \times 0.216= 1.8. \]

Se puede verificar que si una variable aleatoria \(X\) tiene distribución (función de probabilidad) Binomial, \(\text{Bin}(N,p)\), entonces:

\[ \mathbb{E}[X] = Np. \]

Puede consultar cualquier texto de probabilidad para verificar el resultado. El siguiente código muestra como calcular la esperanza para el caso \(\text{Bin}(3,0.6)\), con Python.

from scipy.stats import binom
binom.expect(args=(3,0.6))

1.7999999999999998

Ejercicio

Dé una interpretación al resultado anterior. Observe que 1.8 no corresponde a un valor que pueda tomar la variable aleatoria.

Esperanza de la distribución Poisson

Una variable aleatoria con distribución \(\text{Pois}(\lambda)\) tiene esperanza matemática \(\lambda\).

Ejercicio

Verifique la afirmación anterior.

Varianza y desviación estándar de una variable aleatoria

Varianza

La varianza de una variable aleatoria mide su nivel de predictibilidad. Dicho en otras palabras, que tan dispersos son los valores de la variable aleatoria en relación con la esperanza matemática. Denotemos la esperanza de \(X\) por \(\mu_X\). Técnicamente la varianza de una variable aleatoria se define por:

\[ Var[X] = \mathbb{E}[X-\mu_X]^2 = \sum_{i}p_i (x_i- \mu_X)^2. \]

Desviación estándar

La desviación estándar de una variable aleatoria se denota \(\sigma_X\) y es simplemente la raíz cuadrada de la varianza, es decir:

\[ \sigma_X = \sqrt{Var[X]}. \]

Para entender el porque la varianza mide el nivel de predictibilidad de una variable aleatoria consideremos una variable Bernoulli \(X\). Escribimos \(X \sim \text{Ber}(\pi)\). En este caso puede verificarse que la varianza está dada por:

\[ Var(X) = \pi(1-\pi). \]

El siguiente gráfico muestra la varianza de las distribuciones Bernoulli con valores distintos del parámetro \(\pi\).

import numpy as np
import matplotlib.pyplot as plt

pi = np.linspace(0,1,100)
var = pi*(1-pi)
plt.plot(pi,var)
plt.title('Funcion de varianza de distribciones Bernoulli')
plt.xlabel( '$\pi$')
plt.ylabel('Var')
plt.show()

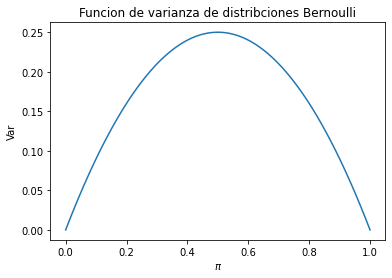
Se observa entonces que la máxima varianza se alcanza para el caso \(\pi=0.5\). Es porque en este caso, es más difícil predecir el resultado del experimento, dado que la probabilidad de acierto y de fallo son la misma. Pero a medida que el valor \(\pi\) está cerca de cero o uno, la varianza desciende hasta cero. Por ejemplo si \(\pi = 0.9\), casi siempre se obtendrá éxito. Esto significa que la variable es más predictible para valores muy altos o muy bajos de \(\pi\). A menor varianza mayor precisión para predecir el resultado del experimento y viceversa.

Entropía de una variable aleatoria

Similar a la varianza, la entropía de una variable aleatoria mide su grado de predictibilidad desde el punto de vista de la teoría de información de Shannon. Dada una variable aleatoria discreta \(X=\{x_1,x_2,\ldots \}\) con función de probabilidad \(p_X =\{p_1, p_2,\ldots \}\), la entropía de \(X\) se define por:

\[ H(X) = -\sum_i p_i\log p_i = -\mathbb{E}[\log P_X] \]

Es usual utilizar la base 2 o la base de los logaritmos Neperianos. En el primer caso, la unidad de medida de la entropía se denomina bit. En el caso de los logaritmos Neperianos, la unidad de medida se acostumbra a llamar nat. En realidad pasar de una base a otra es simplemente un cambio de escala. Estructuralmente miden lo mismo en distintas unidades.

Como en el caso de la varianza ilustramos el concepto para la distribución Bernoulli.

import numpy as np
import matplotlib.pyplot as plt

pi = np.linspace(0.0000001,0.999999,100)
H = -(pi*np.log(pi) + (1-pi)*np.log(1-pi))
plt.plot(pi,H)
plt.title('Entropía de distribuciones Bernoulli')
plt.xlabel( '$\pi$')
plt.ylabel('Entropía')
plt.show()

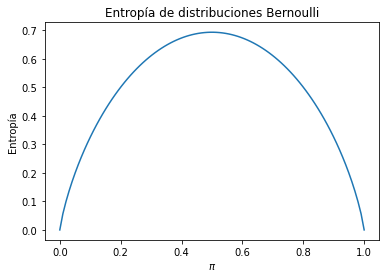
Como se observa la entropía mide de la misma forma que la varianza pero en una escala diferente. Por otro lado observe que en el cálculo de la entropía no se utilizan los valores que toma la variable aleatoria. Solamente se requiere la función de probabilidad de la variable.

En otras palabras se dice que la entropía no depende de la escala de la variable. Solamente de su estructura de probabilidad. Por su parte la varianza sí es dependiente de la escala de la variable aleatoria.

Referencias

1. Alvaro Montenegro y Daniel Montenegro, Inteligencia Artificial y Aprendizaje Profundo, 2021

2. Alvaro Montenegro, Daniel Montenegro y Oleg Jarma, Inteligencia Artificial y Aprendizaje Profundo Avanzado, 2022