Optimización multivariada usando JAX

Introducción

En este ejercicio generamos un conjunto de datos que sigue un modelo lineal, pasando por el origen. Lo datos son contaminado con un error normal \(N(0,2^2)\).

Carga módulos

from __future__ import print_function
import jax.numpy as np # autograd para windows
import numpy as onp
import matplotlib.pyplot as plt
from jax import grad,jit
import pandas as pd

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <cell line: 2>()
      1 from __future__ import print_function
----> 2 import jax.numpy as np # autograd para windows
      3 import numpy as onp
      4 import matplotlib.pyplot as plt

File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\__init__.py:21, in <module>
     18 del _os
     20 # flake8: noqa: F401
---> 21 from .config import config
     22 from .api import (
     23   ad,  # TODO(phawkins): update users to avoid this.
     24   argnums_partial,  # TODO(phawkins): update Haiku to not use this.
   (...)
     87   xla_computation,
     88 )
     89 from .experimental.maps import soft_pmap

File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\config.py:19, in <module>
     17 import threading
     18 from typing import Optional
---> 19 from jax import lib
     21 def bool_env(varname: str, default: bool) -> bool:
     22   """Read an environment variable and interpret it as a boolean.
     23 
     24   True values are (case insensitive): 'y', 'yes', 't', 'true', 'on', and '1';
   (...)
     30   Raises: ValueError if the environment variable is anything else.
     31   """

File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\lib\__init__.py:23, in <module>
      1 # Copyright 2018 Google LLC
      2 #
      3 # Licensed under the Apache License, Version 2.0 (the "License");
   (...)
     15 # This module is largely a wrapper around `jaxlib` that performs version
     16 # checking on import.
     18 __all__ = [
     19   'cuda_prng', 'cusolver', 'rocsolver', 'jaxlib', 'lapack',
     20   'pocketfft', 'pytree', 'tpu_client', 'version', 'xla_client'
     21 ]
---> 23 import jaxlib
     25 # Must be kept in sync with the jaxlib version in build/test-requirements.txt
     26 _minimum_jaxlib_version = (0, 1, 60)

ModuleNotFoundError: No module named 'jaxlib'

Genera y grafica datos simulados

# Simulación de datos

# Elegir una semilla
onp.random.seed(22)

# Generación de los datos
x=onp.linspace(-2,2,100)
y=3*x+5*(onp.random.normal(1,0.3,len(x)))


#Print Results
#print("x:\n",x,"\n")
#print("y:\n",y)

data=pd.DataFrame({"Mediciones":x,"Observaciones":y})
data

	Mediciones	Observaciones
0	-2.000000	-1.137925
1	-1.959596	-3.073814
2	-1.919192	0.865112
3	-1.878788	-0.995351
4	-1.838384	-1.251845
...	...	...
95	1.838384	11.819169
96	1.878788	10.311217
97	1.919192	10.783253
98	1.959596	11.913358
99	2.000000	9.675285

100 rows × 2 columns

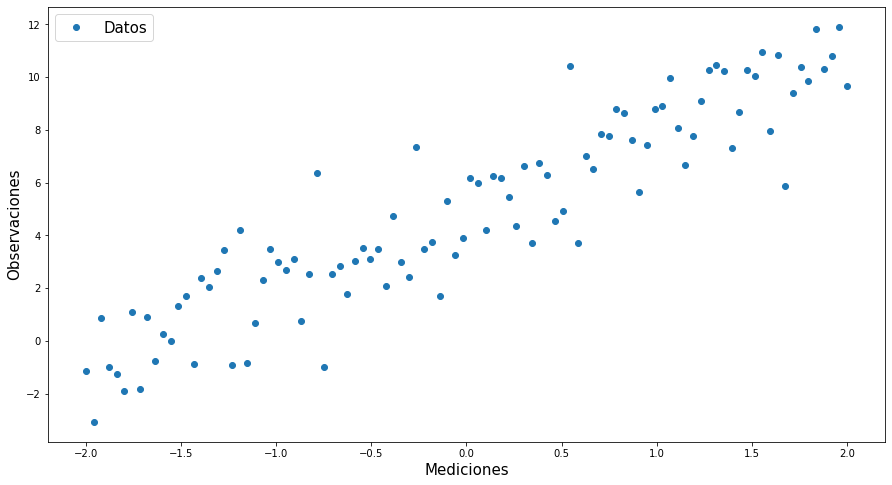
plt.figure(figsize=(15,8))
plt.plot(x,y,'o')
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos"],fontsize=15)
plt.show()

Función de pérdida

def loss(β0,β1,x,y):
    return ((y-(β1*x+β0))**2).mean()

## Diferenciación Automática
grad_loss=jit(grad(loss,argnums=(0,1)))

Gradiente descendiente

def optimize(β0,β1,x,y,h=1.5):
    
    # Calcular Derivada
    β0_grad,β1_grad=grad_loss(β0,β1,x,y)
    
    # Gradiente Descendiente
    β1-=β1_grad*h
    β0-=β0_grad*h
    
    # Regresar Nuevos parámetros
    return β0,β1

Optimización

## Estimación inicial
Β0,Β1=100.,100.

# Acumular resultados
β0,β1=[],[]
train_loss=[]
# Número de veces que se cambiar los parámetros
epochs=300

# Tasa de Aprendizaje
lr=0.01

print("Perdidas:\n")

for epoch in range(epochs):
    
    Β0,Β1=optimize(Β0,Β1,x,y,lr)
    
    β0.append(Β0)
    β1.append(Β1)
    
    losss=loss(Β0,Β1,x,y)
    
    train_loss.append(losss)
    if epoch%10==0:
        print(f"Iteración {epoch}: {losss}")

Perdidas:

Iteración 0: 20803.392578125
Iteración 10: 12779.0595703125
Iteración 20: 7892.66162109375
Iteración 30: 4901.59716796875
Iteración 40: 3060.91064453125
Iteración 50: 1922.00927734375
Iteración 60: 1213.4840087890625
Iteración 70: 770.31201171875
Iteración 80: 491.6375427246094
Iteración 90: 315.49407958984375
Iteración 100: 203.60276794433594
Iteración 110: 132.18850708007812
Iteración 120: 86.40409088134766
Iteración 130: 56.92799758911133
Iteración 140: 37.87733459472656
Iteración 150: 25.52058982849121
Iteración 160: 17.47943115234375
Iteración 170: 12.231060981750488
Iteración 180: 8.796314239501953
Iteración 190: 6.5430588722229
Iteración 200: 5.061695098876953
Iteración 210: 4.085933208465576
Iteración 220: 3.442112922668457
Iteración 230: 3.0166749954223633
Iteración 240: 2.735172748565674
Iteración 250: 2.5486931800842285
Iteración 260: 2.4250361919403076
Iteración 270: 2.342963457107544
Iteración 280: 2.2884490489959717
Iteración 290: 2.2522146701812744

Parámetros finales

print(β1[-1])
print(β0[-1])

2.996511
5.1412616

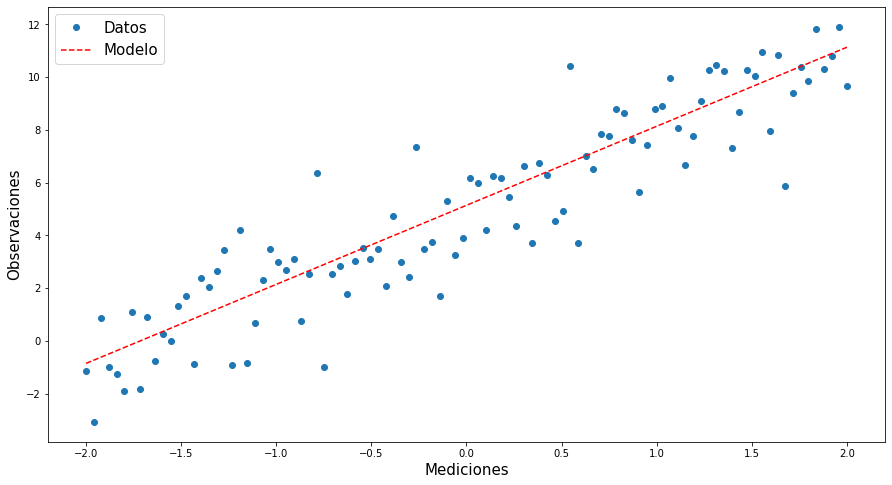
# Haciendo el modelo

mod=β1[-1]*x+β0[-1]

plt.figure(figsize=(15,8))
plt.plot(x,y,'o')
plt.plot(x,mod,'r--')
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos","Modelo"],fontsize=15)
plt.show()

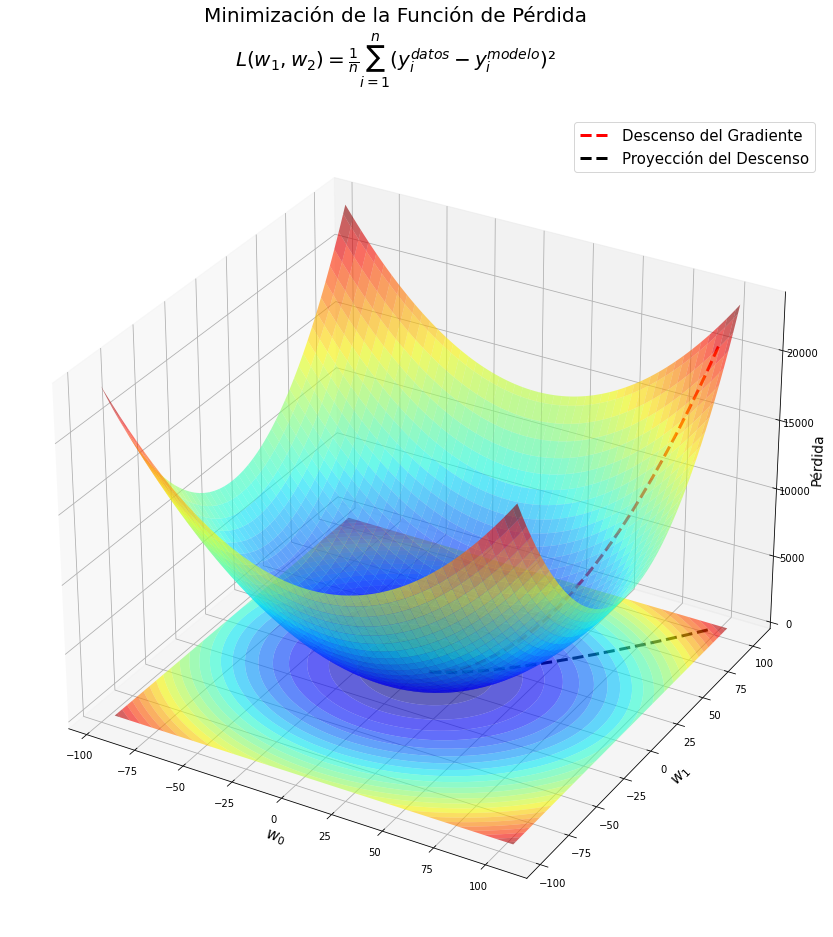
Visualizando la función pérdida

# eje β (par.)
β0x=onp.linspace(β0[-1]-100,β0[-1]+100,100)
β1y=onp.linspace(β1[-1]-100,β1[-1]+100,100)

bx,by=onp.meshgrid(β0x,β1y)

l=onp.empty(shape=(len(β0x),len(β1y)))

for i in range(len(β0x)):
    for j in range(len(β1y)):
        l[i,j]=((by[i,j]*x+bx[i,j]-y)**2).mean()

#%matplotlib inline

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(22,15))
plt.suptitle("Minimización de la Función de Pérdida\n"+r"$L( w_{1}, w_{2})=\frac{1}{n}\sum_{i=1}^{n}(y_i^{datos}-y_i^{modelo})²$",fontsize=20)
ax = plt.axes(projection='3d')

ax.plot_surface(bx,by,l,alpha=0.6,cmap='jet') # Superficie de pérdida

ax.plot(β0,β1,train_loss,'r--',lw=3,label="Descenso del Gradiente") # Ruta tomada por el optimizador
ax.contourf(bx,by,l,25,offset=-1,cmap='jet',alpha=0.6,antialiased=True) # Curvas de nivel de superficie
ax.plot(β0,β1,'k--',lw=3,label="Proyección del Descenso") # Proyección de la ruta

ax.set_xlabel(r"$w_0$",fontsize=15)
ax.set_ylabel(r"$w_1$",fontsize=15)
#ax.zaxis.set_rotate_label(False)  # deshabilitar la rotación automática
ax.set_zlabel("Pérdida",fontsize=14,rotation=90)
#ax.view_init(30, 100)
plt.legend(fontsize=15)
#plt.savefig('GD_3D.png')
plt.show()

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(22,15))
plt.suptitle("Minimización de la Función de Pérdida\n"+r"$L( w_{1}, w_{2})=\frac{1}{n}\sum_{i=1}^{n}(y_i^{datos}-y_i^{modelo})²$",fontsize=20)
ax = plt.axes(projection='3d')

ax.plot_surface(bx,by,l,alpha=0.6,cmap='jet') # Superficie de pérdida

ax.plot(β0,β1,train_loss,'r--',lw=3,label="Descenso del Gradiente") # Ruta tomada por el optimizador
ax.contourf(bx,by,l,25,offset=-1,cmap='jet',alpha=0.6,antialiased=True) # Curvas de nivel de superficie
ax.plot(β0,β1,'k--',lw=3,label="Proyección del Descenso") # Proyección de la ruta

ax.set_xlabel(r"$w_0$",fontsize=15)
ax.set_ylabel(r"$w_1$",fontsize=15)
#ax.zaxis.set_rotate_label(False)  # deshabilitar la rotación automática
ax.set_zlabel("Pérdida",fontsize=14,rotation=90)
#ax.view_init(30, 100)
plt.legend(fontsize=15)
#plt.savefig('GD_3D.png')
plt.show()

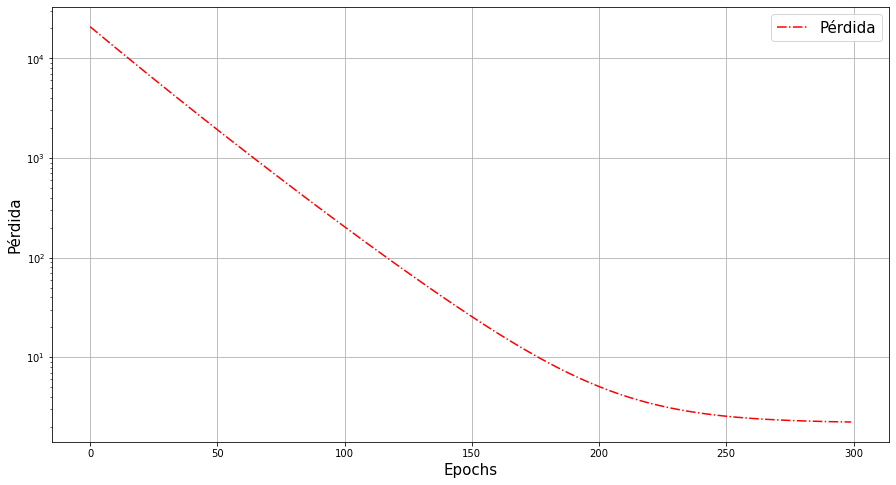
%matplotlib inline
plt.figure(figsize=(15,8))
plt.semilogy(range(epochs),train_loss,'r-.')
plt.xlabel("Epochs",fontsize=15)
plt.ylabel("Pérdida",fontsize=15)
plt.legend(["Pérdida"],fontsize=15)
plt.grid()
plt.show()