Ejemplos de Modelamiento

Introducción a Modelamiento

¿Qué es modelar?

Para aprender este concepto con profundidad, debemos salirnos de la idea de las matemáticas y pensar más en la vida cotidiana.

Pensemos en nuestras emociones.

Si fuéramos un poco juciosos tomando datos cada vez que nos acordemos, digamos 4 veces al día, podríamos obtener información acerca de nuestro día a día.

Supongamos que hacemos alguna vez dicho experimento y escribimos la siguiente información:

---

Fecha	Hora	Emoción
07/02/2020	6:00	Muy feliz
07/02/2020	18:00	Optimista
08/02/2020	7:00	Medio Triste
08/02/2020	20:00	Muy Triste
09/02/2020	9:00	Hambriento
09/02/2020	22:00	Concentrado
10/02/2020	11:00	Concentrado
10/02/2020	23:00	Cansado

Hipótesis del proceso de Modelado

Nuestro objetivo principal dentro del modelado es la descripción y la predicción. Si podemos predecir lo que va a suceder con suficiente anterioridad, ganamos:

• Prevención.

• Planificación.

• Cambio.

• Entendimiento.

Con estas cosas en la mente, tratemos de entender la tabla anterior.

Los humanos estamos llenos de diversas emociones, y tal vez tenerlas todas al mismo tiempo en cuenta puede complicar nuestro entendimiento.

Supongamos entonces, que podemos resumir la siguiente información de emociones y traducirlas en un concepto bipolar (Contento/Triste):

Emoción	Simplificación
Muy feliz	Muy Feliz
Optimista	Medio Feliz
Medio Triste	Medio Triste
Muy Triste	Muy Triste
Hambriento	Poco Triste
Concentrado	Bastante Feliz
Concentrado	Bastante Feliz
Cansado	Medio Triste

Este proceso anterior se conoce como el proceso de hipotetizar el fenómeno a analizar. La idea de generar hipótesis es que podemos de alguna manera ver el problema de manera más sencilla para obtener conclusiones válidas del tema estudiado.

Atención

Este proceso es uno de los más difíciles en el modelado, ya que una hipótesis errónea puede llegar a falsas conclusiones.

Ejemplo Práctico del proceso de Modelado

El arte de poder colocar nuestro conocimiento abstracto en ecuaciones matemáticas fue un gran avance que logró desplazar a la sociedad de su ignorancia de atribuirle eventos que no podían explicar, a eventos que seguían un comportamiento bien definido y predecible.

Tratemos de modelar la tabla anterior:

Para esto, utilicemos una escala que signifique algo cuantitativamente.

Por ejemplo:

Emoción \(\rightarrow [-1,1]\), donde Muy Triste es \(-1\) y Muy Feliz es \(1\).

Al hacer esto, hemos entonces creado un estándar que nos servirá para dar un primer indicio de nuestra información:

Hora	Emoción	Simplificación	Datos
6:00	Muy feliz	Muy Feliz	1
18:00	Optimista	Medio Feliz	0.4
7:00	Medio Triste	Medio Triste	-0.6
20:00	Muy triste	Muy Triste	-0.9
9:00	Hambriento	Poco Triste	-0.1
22:00	Concentrado	Bastante Feliz	0.8
11:00	Concentrado	Bastante Feliz	0.8
23:00	Cansado	Medio Triste	-0.18

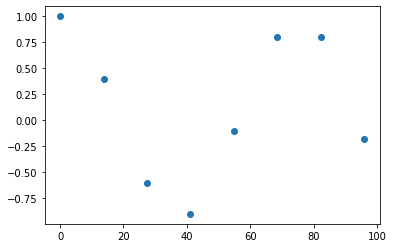
Con esto hecho, ya podemos comenzar a visualizar nuestra información en un gráfico que dice mucho más que mil palabras (o números) en una tabla:

import matplotlib.pyplot as plt
import numpy as np

t = np.array(np.linspace(0,96,8))
E = [1,0.4,-0.6,-0.9,-0.1,0.8,0.8,-0.18]

plt.plot(t,E, marker="o",linestyle="")
#plt.grid()
plt.show()

Construyendo un Modelo Matemático

Ahora que tenemos los datos, podemos comenzar a intentar adivinar que forma tendrán dichos datos para hacer el proceso de predicción.

Dada la forma de los datos, parece que sigue un patrón cíclico.

De nuestra experiencia en matemáticas, podemos inferir que podríamos acomodar una función trigonométrica a dichos datos y esperar que dicho comportamiento se repita para el futuro.

Modelizamos entonces:

\[E(t) = \cos(t)\]

y miramos los resultados:

# Modelo
E_m1 = np.cos(t)

# Verificando modelo
plt.plot(t,E,marker="o",linestyle="",label="observaciones")
plt.plot(t,E_m1,label="modelo")
plt.legend()
plt.show()

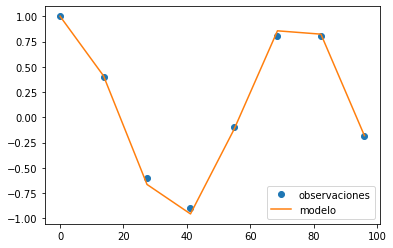
Sin embargo, démonos cuenta de lo siguiente:

La función \(\cos(t)\) se ve más suave que lo que observamos en la gráfica.

¿Será que hay alguna forma de recuperar dicha resolución?

Respuesta: Sí!

# Modelo de mejor resolución
t_m = np.linspace(0,96,10000)
E_m2 = np.cos(t_m)

# Verificando el modelo
plt.plot(t,E,marker="o",linestyle="")
plt.plot(t_m,E_m2)
plt.show()

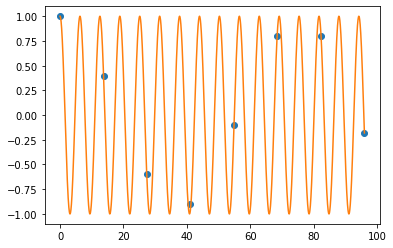
¡Ajá! Entonces, observemos toda la cantidad de información que habíamos estado ignorando todo este tiempo!

La idea del modelamiento, es poder observar esta información perdida, predecir y verificar (validar) que dicho modelo se ajusta bien a nuevos datos no tomados.

Modelo desde Datos Puros

A continuación, trataremos de hacer un modelo que viene desde un valores separados por comas (CSV).

daticos=np.genfromtxt('https://raw.githubusercontent.com/AprendizajeProfundo/Libro-Fundamentos/main/Fundamentacion_Matematica/Datos/datos.csv', delimiter=',')

Veamos algunos valores y su forma:

print("\nPrimeros cinco datos:\n\n","          x               y\n",daticos[0:5,:])
print("\nLos datos tienen forma:",daticos.shape)

Primeros cinco datos:

           x               y
 [[ 0.00000000e+00  1.05203676e+02]
 [ 1.00334448e-01  8.82304968e+01]
 [ 2.00668896e-01  7.87328416e+01]
 [ 3.01003344e-01 -3.60431903e+01]
 [ 4.01337793e-01  1.20883757e+02]]

Los datos tienen forma: (300, 2)

Usando las facilidades de Python, podemos desempaquetar los datos en variables separadas:

x,y=daticos[:,0],daticos[:,1]

Veamos los datos

plt.figure(figsize=(15,7))
plt.plot(x,y,'.')
plt.show()

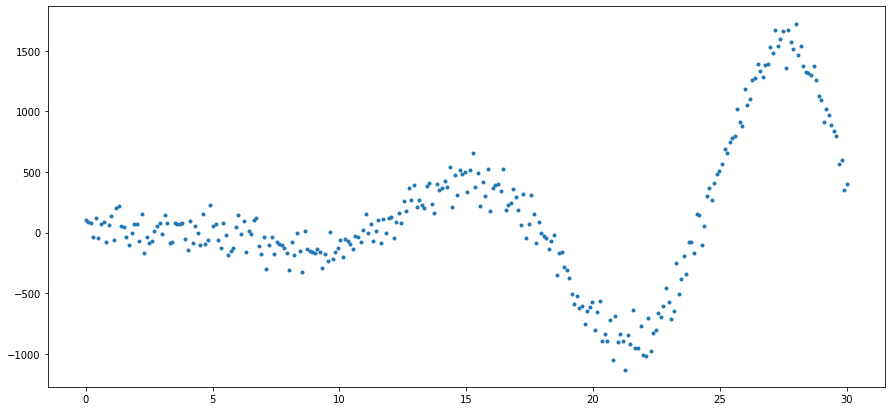
¿Qué opinan?

Usando curve_fit para obtener parámetros (pesos, weights)

Python

from scipy.optimize import curve_fit

# GENERAR EL MODELO
def modelito(x,parametros):
    return # Adivina adivinador

# usando la función curve_fit para hacer el ajuste
pars,_ = curve_fit(modelito(x,y), x, y)

# observar pesos
print(pars)

Python

plt.figure(figsize=(15,7))
plt.plot(x,y,'.')
plt.plot(x,modelito(x,*pars),'b-')
plt.show()

Ejemplos más avanzados

Por supuesto, los ejemplos no se dan únicamente en una dimensión.

Veamos a continuación un ejemplo en 2D:

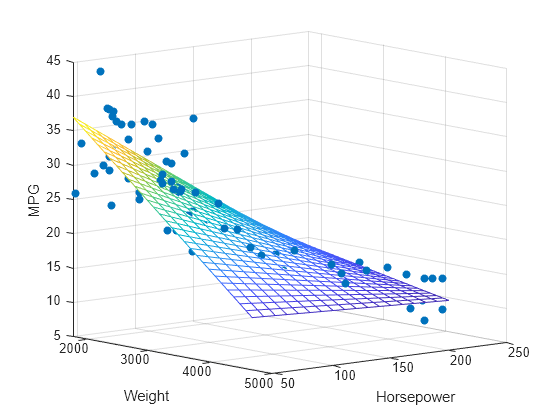
Fuente de la imagen: MathWorks

Catálogo de funciones

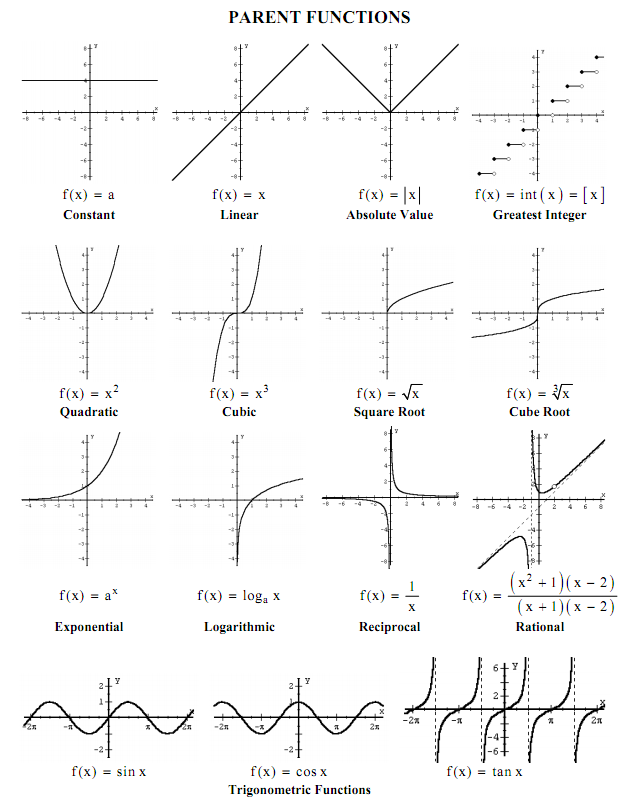
Fuente: Scholars on Mayhew

Fuente: TAMU

Modelos de Clasificación

La problemática general es poder generar un modelo que pueda identificar o clasificar diferentes etiquetas dentro de los datos.

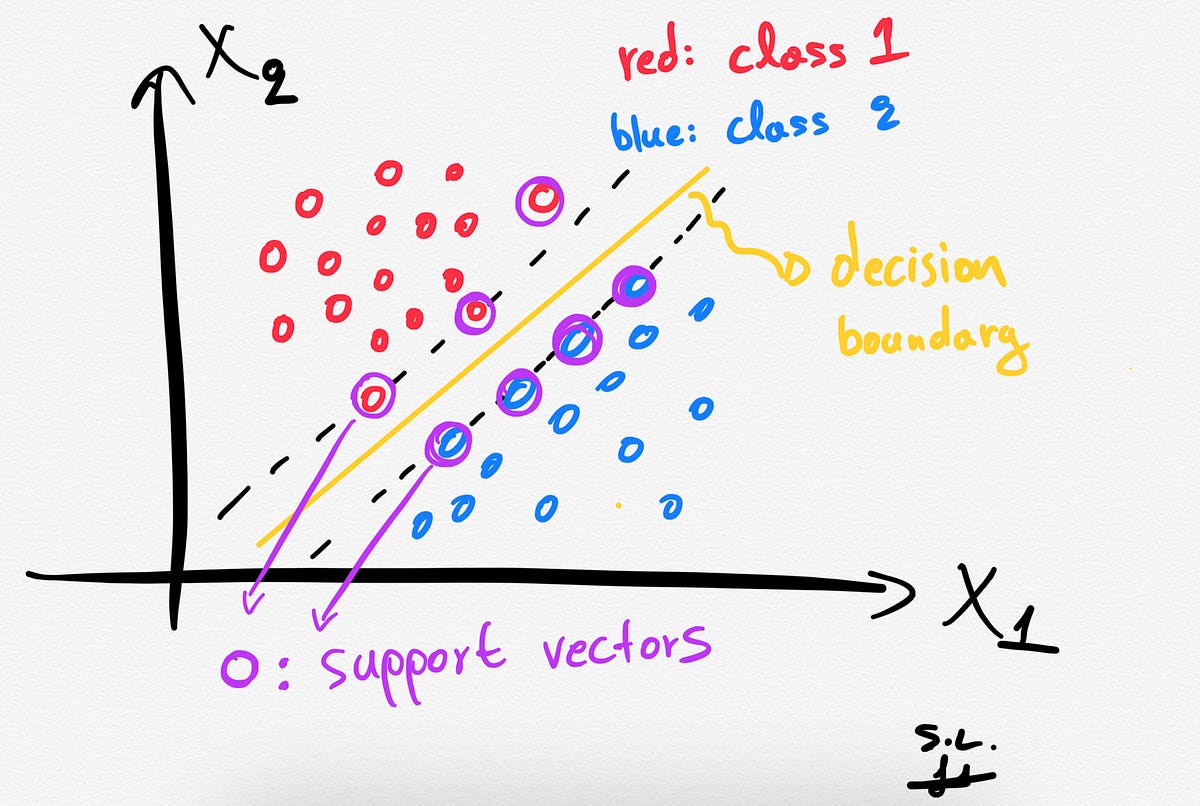
Fuente: Medium

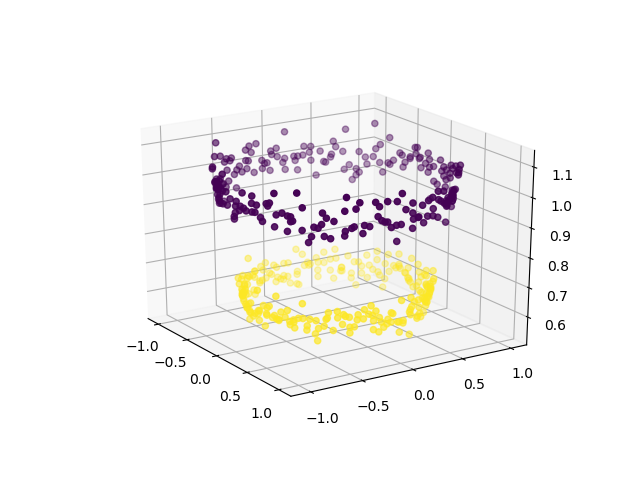
Fuente: Geeks for Geeks

Redes Neuronales

Fuente: Codecademy

Fuente: Medium