Probabilidad

Conceptos básicos

Fuente: Alvaro Montenegro

Introducción

En esta sección se introducen los conceptos básicos de probabilidad requeridos para entender la inteligencia artificial.

El propósito es presentar el lenguaje utilizado. No se hará ningún desarrollo matemático formal. Solamente se presentan los cálculos que se consideren necesarios para entender el concepto.

Espacio muestral

La siguiente gráfica representa un ejemplo de un espacio muestral, el cual denotaremos como \(\mathcal{M}\). Cada objeto dentro de la bolsa es un elemento del espacio muestral. Esto significa que este espacio muestral tiene \(N=20\) elementos. Se supone que cada individuo puede identificarse de manera única. En este ejemplo hemos usado un identificador \(1,2,\ldots,20\), para cada uno de los elementos del espacio muestral.

Adicionalmente, cada individuo tiene un atributo de color. Hay tres colores diferentes: rojo, azul y gris.

Ejemplo de Espacio Muestral M

Evento

Un evento es cualquier subconjunto del espacio muestral. El lector interesado puede verificar, si lo desea, que el espacio muestral \(\mathcal{M}\) tiene exactamente \(2^{20}\) subconjuntos.

Consideremos ahora seis eventos (subconjuntos) especiales de \(\mathcal{M}\):

1. azul: el subconjunto de bolas azules.

2. gris: el subconjunto de bolas grises.

3. rojo: el subconjunto de bolas rojas.

4. pares: el subconjunto de bolas pares.

5. impares: el subconjunto de bolas impares.

6. pares azules: el subconjunto de bolas pares azules.

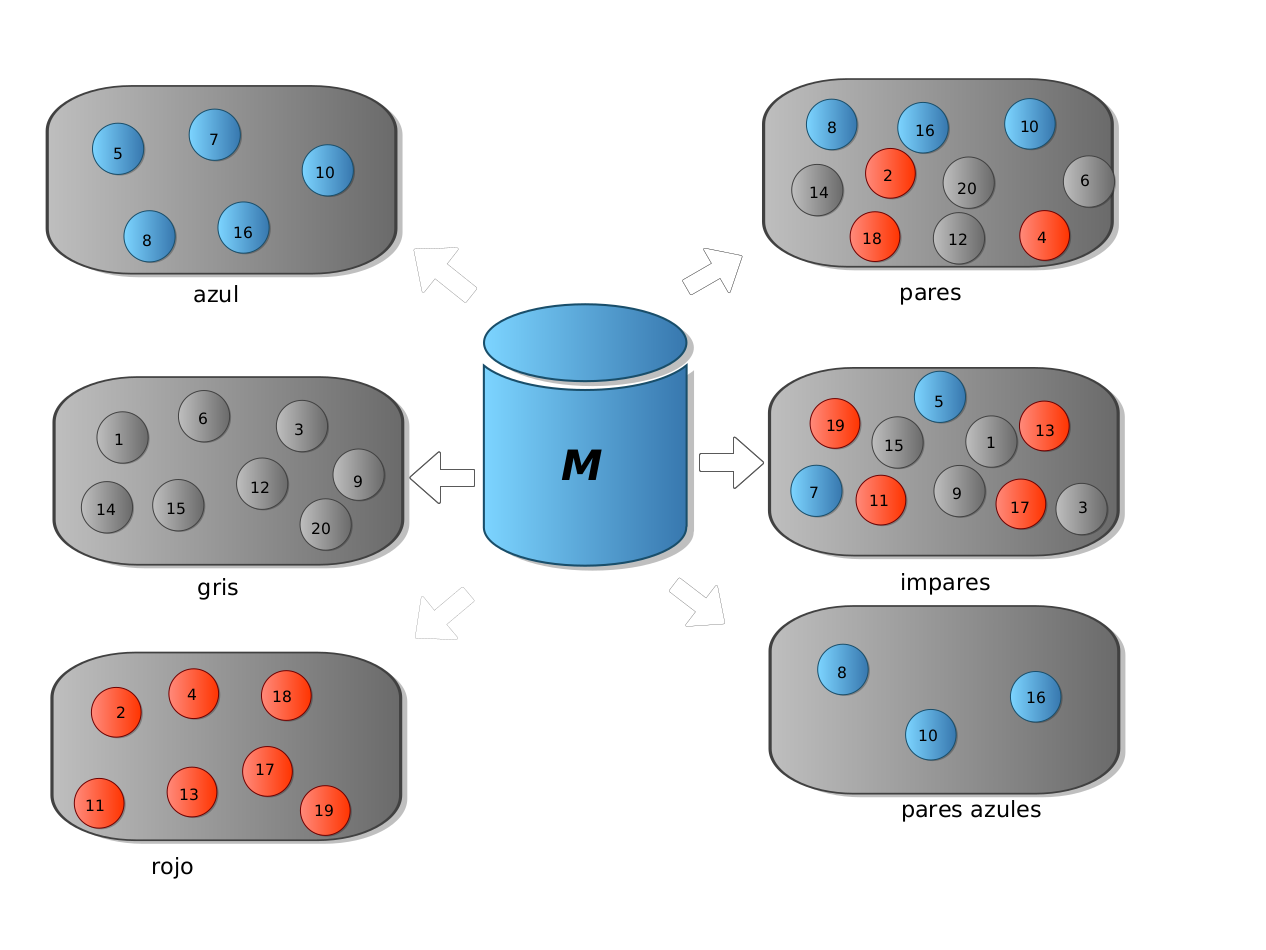
La gráfica muestra los 6 eventos (subconjuntos) del espacio muestral.

Ejemplos de eventos del Espacio Muestral M

Probabilidad

La teoría de probabilidad se creó para poder medir los subconjuntos de una espacio muestral. El concepto de medida en cada caso está asociado a la naturaleza del experimento que se desea modelar (representar de manera abstracta).

En el ejemplo de las bolas presentado arriba, la medida que usaremos será la proporción entre el número de elementos de un evento y el número de elementos del espacio muestral \(M\).

Esto significa que:

\[\begin{split} \begin{align} \text{Prob}[\text{azul}] &= 5/20\\ \text{Prob}[\text{gris}] &= 8/20\\ \text{Prob}[\text{rojo}] &= 7/20\\ \text{Prob}[\text{pares}] &= 10/20\\ \text{Prob}[\text{impares}] &= 10/20\\ \end{align} \end{split}\]

Por favor verifique estos valores. Observe además que \(\text{Prob}[\mathcal{M}] = 1\).

En las siguientes secciones presentamos las propiedades esenciales de la probabilidad, que usaremos a lo largo de nuestro estudio. Son conceptos relativamente sencillos pero muy importantes.

Regla aditiva de la probabilidad

La probabilidad de la unión de dos eventos (subconjuntos) disyuntos (que no tienen intersección) es la suma de la probabilidad (medida) de cada uno de ellos. En símbolos, si \(A\) y \(B\) son eventos disyuntos de \(\mathcal{M}\), entonces:

\[ \text{Prob}[A\cup B] = \text{Prob}[A] + \text{Prob}[B]. \]

Por ejemplo, observe que \(\text{Prob}[\text{azul}\cup\text{rojo}] = 5/20+7/20 = 12/20\). ¿Por qué decimos que azul y rojo son eventos disyuntos?

Sin embargo:

\[ \text{Prob}[\text{azul}\cup\text{pares}] \ne 5/20 + 10/20. \]

Esto se debe a que los eventos azul y pares, no son disyuntos. Como se muestra en la parte inferior derecha de la gráfica de arriba, se tiene que \(\text{Prob}[\text{azul}\cap \text{pares}] = 3/20\). ¿Cómo afecta esta situación el resultado del cálculo de la probabilidad de la unión de dos eventos?

Lo anterior conduce a la regla aditiva general la cual dice que:

\[ \text{Prob}[A\cup B] = \text{Prob}[A] + \text{Prob}[B]-\text{Prob}[A\cap B] . \]

En el ejemplo se tiene entonces que:

\[ \text{Prob}[\text{azul}\cup\text{pares}] = 5/20 + 10/20 - 3/20 = 12/20 \]

Ejercicio

¿Qué piensa de la siguiente afirmación? ¿Es verdadera o es falsa? Justifique su respuesta.

Si \(A\) y \(B\) son conjuntos disyuntos, entonces \(\text{Prob}[A\cap B] = 0\).

Medida de todo el espacio muestral

Vamos a denotar por \(\emptyset\) al conjunto vacío, es decir un conjunto que no tiene elementos.

En nuestro ejemplo tenemos que:

\[\mathcal{M}= \text{azul}\cup \text{rojo}\cup \text{gris}\]

Además se tiene que:

\[\begin{split} \begin{align} \text{azul}\cap \text{rojo} &= \emptyset\\ \text{azul}\cap \text{gris} &= \emptyset\\ \text{gris}\cap \text{rojo} &= \emptyset\\ \end{align} \end{split}\]

Se dice en esta situación que los conjuntos son mutuamente excluyentes. De acuerdo con la regla aditiva tenemos que:

\[ \text{Prob}[\mathcal{M}] = \text{Prob}[\text{azul}] + \text{Prob}[\text{rojo}]+ \text{Prob}[\text{gris}] = 5/20 + 7/20 + 8/20 = 1. \]

Esta es una propiedad general de la probabilidad. El espacio muestral siempre tiene medida de probabilidad 1.

Además observe que si se tienen eventos disyuntos entre sí (mutuamente excluyentes), cuya unión es el espacio muestral, entonces la probabilidad de la unión de todos esos eventos tiene probabilidad 1.

Probabilidad del complemento de un evento

El complemento de un evento \(A\) se denotará por \(A^{c}\). Este simplemente es el conjunto de elementos del espacio muestral que están por fuera de \(A\). Entonces, es inmediato que \(\mathcal{M} = A\cup A^c\). Por lo que:

\[ Prob[A^c] = 1 - Prob[A]. \]

Una consecuencia inmediata de esta propiedad es que como \(\mathcal{M}^c= \emptyset\), porque el espacio muestral contiene a todos los elementos, entonces \(Prob[\emptyset]=0\).

En nuestro ejemplo \(impares^c= pares\). Entonces \(Prob[\text{impares} ] = 1- 10/20 = 10/20\). Por favor verifique este resultado.

Probabilidad condicional

El concepto de probabilidad condicional es de vital importancia en el estudio del aprendizaje profundo y la inteligencia artificial.

Como el nombre parece indicar, se trata de calcular la probabilidad de un evento que está sujeto a una restricción. En realidad es así y la restricción normalmente está asociada con otro evento.

Para ilustrar el asunto, supongamos que se pregunta por la probabilidad que una bola extraída sea par, dado que la bola es azul.

Se observa entonces, que se da una información antes de calcular la probabilidad de ser par. Esta información corresponde al evento azul. Escribiremos:

\[ \text{Prob}(\text{par}|\text{azul}) \]

Para hacer el cálculo correcto, se procede de la siguiente manera:

Primero se reduce el espacio muestral a azul. En el ejemplo se tiene que:

\[ \text{azul} = \{5,7,8,10,16 \}. \]

Ahora que se ha restringido el espacio muestral a azul, se calcula la probabilidad de interés. En este caso par. Observe entonces que:

\[ \text{Prob}(\text{par}|\text{azul}) = \tfrac{3}{5} \]

Porque en el evento azul que tiene 5 elementos, hay 3 de estos pares.

Puede verificarse que:

\[ \text{Prob}(\text{par}|\text{azul}) = \frac{\text{Prob}[\text{par}\cap \text{azul}]}{\text{Prob}[\text{azul}]} \]

Ejercicio

Imagínese como se podría verificar esta última ecuación. Calcule \(\text{Prob}(\text{par}|\text{azul})\) usando dicha ecuación.

Esta es una regla general, que se enuncia así: Si \(A\) y \(B\) son eventos del espacio muestral \(\mathcal{M}\), entonces se define \(\text{Prob}[A|B]\) como:

\[ \text{Prob}[A|B] = \frac{\text{Prob}[A\cap B]}{\text{Prob}[B]} \]

Regla multiplicativa de la probabilidad

De la definición de la probabilidad condicional \(\text{Prob}[A|B]\) se desprende que:

\[ \text{Prob}[A\cap B] = \text{Prob}[B]\times \text{Prob}[A|B] \]

Ejemplo

Con nuestro ejemplo supongamos que se pregunta por la probabilidad de obtener una bola par azul en un experimento.

La solución es sencilla, porque ya hemos obtenido que \(\text{Prob}(\text{par}|\text{azul}) = \tfrac{3}{5}\), y \(\text{Prob}[\text{azul}] = \tfrac{5}{20}\). por lo tanto:

\[ \text{Prob}[\text{par}\cap\text{azul}] = \text{Prob}[\text{azul}]\times\text{Prob}[\text{par}|\text{azul}] = \tfrac{5}{20}\times \tfrac{3}{5} = \tfrac{3}{20} \]

Esto está de acuerdo con la ilustración de los evento del espacio muestral exhibidos arriba.

Independencia

Dos eventos \(A\) y \(B\) del espacio muestral \(\mathcal{M}\) se dicen independientes si:

\[ \text{Prob}[A\cap B] = \text{Prob}[A] \times\text{Prob}[B]. \]

Esta definición es bastante técnica, pero intuitivamente puede entenderse como que la ocurrencia de un evento no afecta la ocurrencia del otro. Observe que en este caso se tiene que:

\[ \text{Prob}[A| B] = \text{Prob}[A]. \]

Ejercicio

Por favor verifique esta última afirmación.

Ejercicios

Considere el siguiente experimento. Se lanzan dos dados no cargados de seis caras cada uno. El resultado del experimento es una pareja de números. Por ejemplo \((6,4)\).

Fuente: pixabay

1. Haga una tabla, usando Markdown con todo el espacio muestral \(\mathcal{M}\). Ayuda: son 36 elementos.

2. ¿Cuántos eventos son posibles? Use Python para hacer el cálculo.

3. Calcule la probabilidad de obtener 2,3,…,12.

4. Calcule la probabilidad de obtener un número par.

5. Compruebe que la probabilidad de obtener 5 en el dado blanco es 1/5 y que este evento es independiente del valor obtenido en el dado negro.

6. Escriba un programa en Python que construya un tensor de dimensión 2 y que contenga los 36 posibles resultados. Consulte sobre como se hace un ciclo for en Python.

Referencias

1. Alvaro Montenegro y Daniel Montenegro, Inteligencia Artificial y Aprendizaje Profundo, 2021

2. Alvaro Montenegro, Daniel Montenegro y Oleg Jarma, Inteligencia Artificial y Aprendizaje Profundo Avanzado, 2022