Introducción a la Derivación#

Introducción#

Las matemáticas han jugado un papel fundamental en la historia de la humanidad.

Desde la predicción de eventos astronómicos, yendo por el establecimiento de un modelo económico más o menos estable, hasta el acortamiento de la segunda guerra mundial y la implementación tangible de la inteligencia artificial.

Recordemos que el conocimiento es poder. Por lo tanto, es natural que el ser humano haya concentrado gran parte de su tiempo en acumular conocimiento para poder controlar la sociedad y brindarle un orden.

El conocimiento enseña, moldea y permite crecer.

Pero más que un conocimiento puro sobre las cosas, la matemática guía el camino del conocimiento hacia un sendero fortuito: la capacidad de predecir el futuro.

Concepto de Derivada#

A comparación de todo lo que se pudiese pensar, las matemáticas están en todas partes.

En particular, el concepto de derivada lo experimentamos todos los días, en todo momento.

Esto es debido al hecho de que la derivada es el mismísimo concepto de la percepción de cambio o movimiento.

Si podemos percibir el presente y el pasado, podemos notar que cambios hubo, comparando nuestro presente con nuestro pasado.

Son precisamente esos cambios, respecto a una escala de medición (por ejemplo, el tiempo), lo que consideramos una razón de cambio.

Ejemplos:

  • Salir a correr y medir el tiempo que ha tardado cada 100 metros.

  • Subir o bajar el volumen de su equipo de sonido con una perilla, midiendo ángulos y tiempo.

  • Hacer un censo en su barrio cada año.

  • Contar el número de flores que encuentre cada metro cuadrado desde un punto de referencia y en forma rectangular.

  • Mida en intervalos de tiempo de 10 segundos la temperatura de su café hasta que esté frío por completo.

Ahora, si se pudiesen medir todas estas cosas, pero de manera muy rápida (algo cuestionable, pero ideal), el resultado de ese cambio instantáneo es lo que se conoce como la derivada de una cantidad respecto a otra.

Intuición#

Hay derivadas en todo lo que hacemos.

Averigue sobre el concepto del Tao y conciencia del movimiento.

  • Imagine que está caminando por la calle.

  • Sea consciente de su movimiento.

  • ¿Va lento?, ¿Va tarde?, ¿Debe ir más rápido para tomar el bus?

  • Respire. Corra. Sea Consciente. Reflexione.

  • Ir más rápido acelera el pulso de su corazón.

  • Descanse en el bus. Hay quietud.

Las cosas que alteran los estado naturales de las cosas, esos cambios, son percibidos por nuestra mente de manera continua.

Tómese el tiempo para reflexionar sobre si ha sido consciente durante su vida en los cambios que están a su alrededor.

Si no lo ha hecho, ya viene siendo hora.

Cómo entender las Matemáticas

Concepto Geométrico#

Dibujos ilustrativos del cambio#

Lenguaje Matemático#

Definición matemática#

\[\frac{df}{dx}=f'(x)=\lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x}= \lim_{\text{cambio en x va a cero}}\frac{\text{cambio en f}}{\text{cambio en x}}\]

Ese \(\lim_{\Delta x \to 0}\) no es nada más que la manera formal de decir:

«Estoy tomando muchas mediciones, muy rápido. Tan rápido que no puedo percibir donde termina una y donde comienza otra».

Cuidado

No todas las funciones se pueden derivar bajo esta definición. Las más inocentes funciones pueden fallar en tener una derivada clásica consistente. Sin embargo, los matemáticos se han encargado de incursionar en estas profundidades de lo extraño y, desde el siglo XX, ya fue posible derivar casi todo, usando un concepto llamado Derivada Distribucional. Este concepto se sale del alcance de este curso, pero es bastante interesante.

Sin entrar en los detalles, podemos plasmar algunas propiedades de esta derivada:

  • \((f\pm g)'=f'\pm g'\) (Divide y Conquista)

  • \((f\cdot g)'=f'g+fg'\) (Cada cosa tiene su cambio)

  • \((\frac{f}{g})'=\frac{f'g-fg'}{g^2}\) (WTF property)

  • \((f \circ g)'= f'(g)\cdot g'=\frac{df}{dg}\frac{dg}{dx}\) (Chain’s Rule, regla de la cadena)

De todas las anteriores, la más importante es quizá la regla de la cadena.

Esta nos asegura una verdad muy interesante:

No importa que tan complicada sea tu función derivable, podrás derivar, siempre y cuando lo hagas bien.

Por eso enseñamos cálculo diferencial, pues muchas funciones son posible derivarlas. No importa que tan largo, que tan alto, siempre podremos escrudiñar desde afuera hacia adentro y encontrar una respuesta final.

Todo se convierte a la final, en multiplicaciones, sumas (o restas) y quizá divisiones.

Este hecho es muy importante, pues es la base de lo que hoy se conoce como Diferenciación Automática.

Derivada como Aproximación Lineal#

Una forma, quizá más ilustrativa de entender la derivada, es que resume comportamientos complejos en términos de líneas rectas.

En dimensiones superiores, serán hiperplanos.

O sea, en vez de analizar una función complicada, podemos usar las derivadas en cada uno de sus puntos para saber su comportamiento cercano.

En términos matemáticos: La derivada es la mejor aproximación lineal de una función en un punto dado.

Fuente: AWS

Formas de Cálculo#

Derivada Simbólica #

Si bien la definición de límite puede llegar a ser algo fastidiosa y tediosa, mediante ella se han logrado hallar varias derivadas:

\[\frac{d(\text{número})}{dx}=0\]
\[\frac{d(x)}{dx}=1\]
\[\frac{d(w_1x+w_0)}{dx}=w_1\]
\[\frac{d(w_2x^2+w_1x+w_0)}{dx}=2w_2x+w_1\]
\[\dots\]
\[\frac{d(x^n)}{dx}=nx^{n-1}\]

Y así, hay muchas más…

Sin embargo, este no es un curso de cálculo diferencial.

Para los interesados, pueden ver la tabla de las derivadas más comunes aquí.

De todas maneras, es posible obtener un paquete para realizar derivación simbólica. Por ejemplo, usando el paquete sympy de Python.

Ejemplo#

# pip install sympy

from sympy import *
x, y, z = symbols('x y z')
init_printing(use_unicode=True)

print("\ncos(x)' =",diff(cos(x), x),"\n")

diff(exp(x**2), x)

cos(x)' = -sin(x)
../../_images/cal_derivadas_25_1.png

Calculemos, por ejemplo:

\[\frac{\partial^7}{\partial x\partial y^2\partial z^4} e^{x y z}\]
expr = exp(x*y*z)
diff(expr, x, y, y, z, z, z, z)
../../_images/cal_derivadas_27_0.png

Derivada Numérica#

Como pudimos observar en la definición matemática de la derivada, se hace necesario usar la maquinaria de un objeto abstracto llamado límite.

Sin embargo, para calcular un límite en la vida real, tendríamos que recolectar información infinitamente cerca entre mediciones, lo cual no es manejable para un computador.

Para estos propósitos, se puede hablar de un concepto numérico: No es necesario calcular un límite, pero sí

\[f'(x_i)\approx \frac{\Delta f }{\Delta x}\bigg|_{x_{i}}=\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}\]

Donde dicho cociente representa el cambio entre mediciones sucesivas. No se pone \(\Delta x\), pues no necesariamente las mediciones fueron tomadas de manera uniforme.

Este procedimiento es conocido como diferencias finitas, y es muy útil por ejemplo, para solucionar ecuaciones diferenciales (ordinarias o parciales).

Fuente: Wikipedia

Ejemplo#

import numpy as np
import matplotlib.pyplot as plt

def Num_Der(x,y):
    
    x=np.array(x)
    y=np.array(y)
    n=len(x)-1
    ΔyΔx=np.empty(n)
    
    for i in range(n):
        
        Δx=x[i+1]-x[i]
        Δy=y[i+1]-y[i]
        ΔyΔx[i]=Δy/Δx
        
    return ΔyΔx

x=np.linspace(-10,10,100)
f=x**2*np.sin(x)#+np.random.normal(0,0.01,len(x))

df=Num_Der(x,f)

plt.figure(figsize=(15,8))
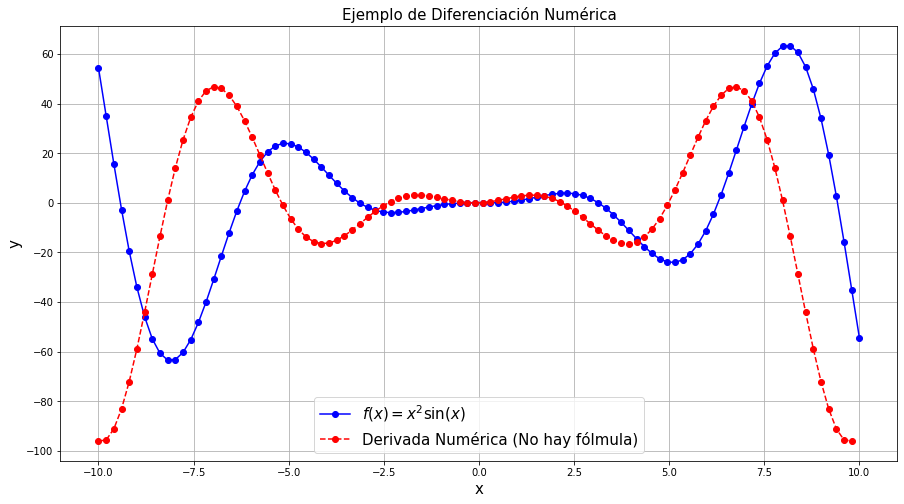
plt.title("Ejemplo de Diferenciación Numérica",fontsize=15)
plt.plot(x,f,'bo-',label="$f(x)=x^2\sin(x)$")
plt.plot(x[:-1],df,'ro--',label="Derivada Numérica (No hay fólmula)")
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.legend(fontsize=15)
plt.grid()
plt.show()
../../_images/cal_derivadas_32_0.png 
x = symbols('x')
diff(x**2*sin(x), x)
../../_images/cal_derivadas_33_0.png

Diferenciación Automática#

El problema con los tipos anteriores de calcular derivadas es que, si bien puede ser un trauma la matemática de colegio y es un gran filtro para carreras en ciencias, el no poder derivar simbólicamente de manera correcta en los primeros semestres de universidad, es que su implementación computacional no es el más eficiente debido al tiempo que este tarda en devolver una respuesta.

Por otro lado, como vimos, la derivada numérica puede ser objeto de abusos computacionales como es la pérdida de precisión y hasta la cancelación catastrófica.

También, si los datos que manejamos tienen ruido o incertidumbre, eso se replicará de forma amplificada en la derivada numérica.

Recordemos que para nuestros propósitos de Aprendizaje Profundo, queremos calcular derivadas (Ya veremos porqué), pero no queremos perder precisión en el camino y menos aún sabiendo que estimaremos millones, quizá billones de parámetros.

Hay algo más inteligente que podemos hacer al respecto, y eso es usar un paquete que permita derivar de manera automática (Gracias Regla de la Cadena).

Más adelante se hará una introducción propia a este concepto, que es bastante interesante (y de hecho es la espina dorsal del Aprendizaje Profundo), por lo que tan sólo se ilustrará mediante gráfico y se hará un ejemplo.

Fuente: Wikipedia

Ejemplo#

from jax import grad,jit,vmap
import jax.numpy as jnp

x=jnp.linspace(-5,5,100)
grad_f=jit(vmap(grad(jnp.tanh)))
g2=jit(vmap(grad(grad(jnp.tanh))))
g3=jit(vmap(grad(grad(grad(jnp.tanh)))))

plt.figure(figsize=(15,8))
#plt.plot(x,y,'o')
plt.plot(x,np.tanh(x))
plt.plot(x,grad_f(x))
plt.plot(x,g2(x))
plt.plot(x,g3(x))

plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos"],fontsize=15)
plt.grid()
plt.show()

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [5], in <cell line: 1>()
----> 1 from jax import grad,jit,vmap
      2 import jax.numpy as jnp
      4 x=jnp.linspace(-5,5,100)

File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\__init__.py:21, in <module>
     18 del _os
     20 # flake8: noqa: F401
---> 21 from .config import config
     22 from .api import (
     23   ad,  # TODO(phawkins): update users to avoid this.
     24   argnums_partial,  # TODO(phawkins): update Haiku to not use this.
   (...)
     87   xla_computation,
     88 )
     89 from .experimental.maps import soft_pmap

File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\config.py:19, in <module>
     17 import threading
     18 from typing import Optional
---> 19 from jax import lib
     21 def bool_env(varname: str, default: bool) -> bool:
     22   """Read an environment variable and interpret it as a boolean.
     23 
     24   True values are (case insensitive): 'y', 'yes', 't', 'true', 'on', and '1';
   (...)
     30   Raises: ValueError if the environment variable is anything else.
     31   """

File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\lib\__init__.py:23, in <module>
      1 # Copyright 2018 Google LLC
      2 #
      3 # Licensed under the Apache License, Version 2.0 (the "License");
   (...)
     15 # This module is largely a wrapper around `jaxlib` that performs version
     16 # checking on import.
     18 __all__ = [
     19   'cuda_prng', 'cusolver', 'rocsolver', 'jaxlib', 'lapack',
     20   'pocketfft', 'pytree', 'tpu_client', 'version', 'xla_client'
     21 ]
---> 23 import jaxlib
     25 # Must be kept in sync with the jaxlib version in build/test-requirements.txt
     26 _minimum_jaxlib_version = (0, 1, 60)

ModuleNotFoundError: No module named 'jaxlib'

Referencias#