Breve introducción a R

Nota

Los trozos de código de esta página son de R. Por favor, ejecútelos en Colab o Binder

Introducción

¿Qué es R y para qué es usado?

R es un lenguaje de programación y entorno computacional distribuido de manera gratuita, a través de la Licencia Pública General de GNU, por lo que es software libre y de código abierto. R es diferente a otros lenguajes de programación que por lo general están diseñados para realizar muchas tareas diferentes; esto es porque fue creado con el propósito de hacer estadística, para personas con experiencia en otros lenguajes puede resultar extraño en algunos sentidos, pero también es la razón por la que R es una herramienta muy poderosa para el trabajo en estadística, puesto que funciona de la manera que una persona especializada en esta disciplina desearía que lo hiciera.

R tiene sus orígenes en S, un lenguaje de programación creado en los Laboratorios Bell de Estados Unidos. Dado a las restricciones de uso Ross Ihaka y Robert Gentleman, de la Universidad de Auckland en Nueva Zelanda, decidieron crear una implementación abierta y gratuita de S, trabajo que inició en 1992 y que tuvo una versión estable en 2000. R es un lenguaje relativamente joven pero que ha experimentado un crecimiento acelerado en su adopción durante los últimos 10 años ya que permite responder preguntas mediante el uso de datos de forma efectiva, y compartir y generar código en comunidad.

Sus principales usos son en los campos de aprendizaje automático (machine learning), minería de datos, investigación biomédica, bioinformática y matemáticas financieras. Sin embargo, con el paso del tiempo los usuarios de este lenguaje han creado extensiones a R, llamadas paquetes, que han ampliado su funcionalidad. En la actualidad es posible realizar en R minería de textos, procesamiento de imagen, visualizaciones interactivas de datos y procesamiento de Big Data, entre muchas otras cosas.

Instalación

CRAN: The Comprehensive R Archive Network. Ahí se archivan todas las versiones de R base, así como todos los paquetes para R que han pasado por un proceso de revisión riguroso, realizado por el CRAN Team, que se encarga de asegurar su correcto funcionamiento.

Una vez instalado R en nuestro computador, tenemos la consola en los trozos de código de Notebook. Sumemos dos números:

123+876

999

Corriendo R desde una terminal del sistema opertativo tenemos lo mismo. Se arranca tecleando R y q() Termina el programa R. Abrir la terminal y arrancar R.

Características

Para presentar el lenguaje estadístico R, utilizo el artículo Facets of R (Chambers 2009), donde el autor resume las principales características de R en seis facetas, que son también resumen de parte de su historia:

1. Una interfaz de procedimientos computacionales de muchos tipos.

2. Interactivo: se ejecuta en tiempo real.

3. Funcional en su modelo de programación.

4. Orientado a objetos: todo es un objeto.

5. Modular: construido en piezas estandarizadas.

6. Colaborativo: un esfuerzo mundial de código abierto.

Chambers presenta las facetas en parejas:

Una interfaz interactiva

• Una mejor interfaz para los procedimientos computacionales nuevos para el análisis de datos científicos, por lo general implementados como subrutinas Fortran, luego también en C y otros lenguajes. Por ejemplo LACPAC

• La investigación estadística de Bell Labs había recogido y escrito una variedad procedimientos en Fortran.

• Se publicaban algoritmos para muchas de las técnicas computacionales esenciales.

• Estos procedimientos fueron la esencia de los análisis de datos reales.

• La interfaz tenía que ser interactiva.

• Un lenguaje usado para que el analista de datos se pueda comunicar en tiempo real con el software.

Funcional en su modelo de programación y orientado a objetos, «todo es un objeto»

• Los procedimientos son funciones.

• La interfaz de procedimiento se define como funciones que proveen una interfaz para subrutinas en Fortran o C.

• Se incluyen clases de objetos y métodos que hacen que las funciones específicas funcionen de acuerdo a las clases de sus argumentos. Por ejemplo, la función diag() que se ve a continuación.

• Funciones como objetos.

• Los objetos tienen un atributo que define su clase.

• S4 provee definiciones formales de las clases.

• Definiciones formales de métodos asociados con funciones genéricas.

a = c(1:4);a;class(a)         #vector
A <- matrix(a,2,2);A;class(A) #matriz
print("Diagonal A")
diag(A)                       #diag cuando el argumento es una matrix
print("Matriz identidad orden 3")
diag(3) -> I3;I3;class(I3)    #Asignación a I3 una matriz identidad de orden 3 

1. 1
2. 2
3. 3
4. 4

'integer'

A matrix: 2 × 2 of type int

1	3
2	4

1. 'matrix'
2. 'array'

[1] "Diagonal A"

1. 1
2. 4

[1] "Matriz identidad orden 3"

A matrix: 3 × 3 of type dbl

1	0	0
0	1	0
0	0	1

1. 'matrix'
2. 'array'

Modular, construido a partir de piezas estandarizadas

• Colaboración: un esfuerzo de código abierto en todo el mundo.

• Funciones y paquetes.

• Entorno (environment)

• Funciones comparten ambiente, mecanismo Namespace.

• Un paquete R es un módulo que combina funciones de R, su documentación y posiblemente datos y código en otros lenguajes.

• R está disponible libremente como un sistema de código abierto: tanto el programa núcleo como la mayoría de los paquetes, que son el resultado de nuevas investigaciones estadísticas y sus aplicaciones. Actulmente (marzo de 2021) hay más de 17 paquetes en el CRAN de R.

• Las herramientas para la administración de paquetes juegan un papel esencial de colaboración.

• R generalmente es capaz de incorporar otros softwares de código abierto o relacionarse con ellos, por ejemplo:

  • LATEX

  • xfig

Cómo empezar y avanzar en R

Para quienes van a abordar R desde este ambiento de Jupyter, se recomienda leer poco a poco en la documentación que queda disponible al instalar R. Lo primero es Introducción a R.

help.start()

starting httpd help server ...

 done

If nothing happens, you should open
'http://127.0.0.1:19986/doc/html/index.html' yourself

Para empezar a interactuar con R, ir al Apéndice A del documento de introducción a R, ir leyendo y copiando cada comando aquÍ. Por ejemplo el 1ro:

1. help.start(): ya lo hicimos

Vamos a continuar con la introducción a R, sin embargo, se recomienda ver las referencias del documento.

fruta <- c(5, 10, 1, 20)  #vector
names(fruta) <- c("naranja", "plátano", "manzana", "pera") #asignar nombres de los elementos del vector
fruta

naranja

5

plátano

10

manzana

1

pera

20

Lst <- list(nombre="Pedro",      #lista
            esposa="María",
            no.hijos=3,
            edad.hijos=c(4,7,9))
Lst

$nombre

'Pedro'

$esposa

'María'

$no.hijos

3

$edad.hijos

1. 4
2. 7
3. 9

for (i in fruta) #los vectores son iterables
    print (i)
cat("\n")
for (i in Lst) #las listas son iterables
    print (i)

[1] 5
[1] 10
[1] 1
[1] 20

[1] "Pedro"
[1] "María"
[1] 3
[1] 4 7 9

Como sabemos la clase de los objetos?

class(fruta)
class(Lst)
class(-17+0i)

'numeric'

'list'

'complex'

sqrt(-17)
sqrt(-17+0i) #admite números complejos

Warning message in sqrt(-17):
"NaNs produced"

NaN

0+4.12310562561766i

Para saber sobre la función y sus argumentos se pueden utilizar cualquiera de las siguientes dos opciones:

#help(sqrt)
#?sqrt

Veamos como utilizar la función sqrt en la siguiente función, hagamos una función para calcular la desviación estándar muestral:

StdErr <- function(x)
    sqrt(sum((x-mean(x))^2)/(length(x)-1))

StdErr(1:10)

3.02765035409749

sd(1:10)

3.02765035409749

Algunas funciones para estadística

Dentro de las muchas funciones se encuentra la función beta (beta), binomial (binom), Cauchy (cauchy), ji cuadrado (chisq), exponencial (exp), F de Snedecor (f), gamma (gamma),geométrica (geom), entre otras. Para saber más puede revisar en el capítulo 8-Distribuciones probabilísticas.

set.seed(23)
x <- rnorm(50, mean=0, sd=1) #muestra normal de 
y <- rnorm(x)
plot(x, y, main="x vs y")

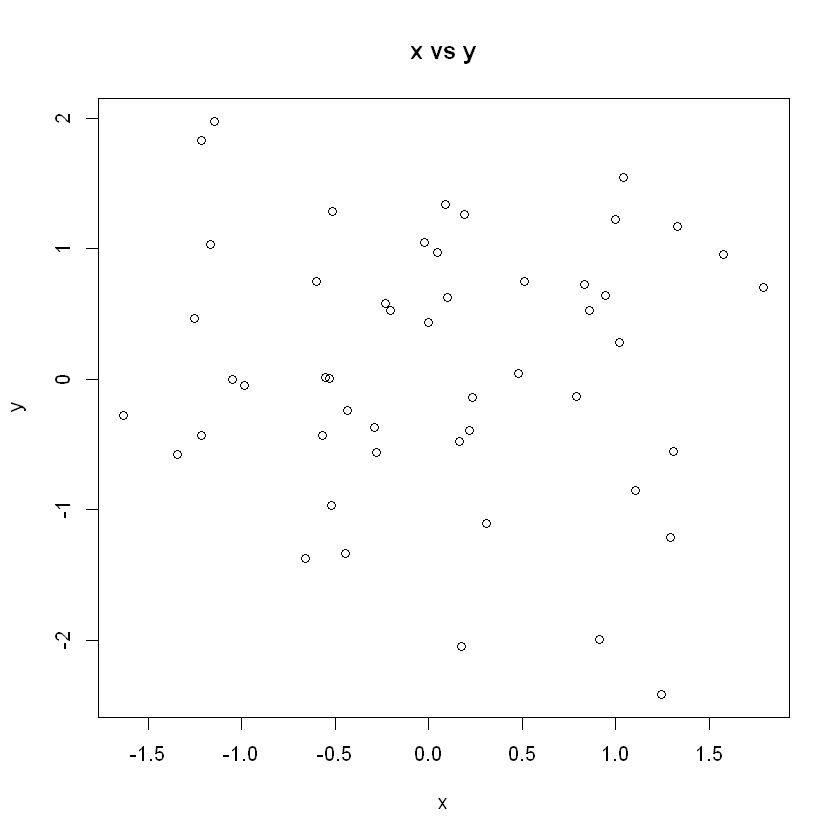
Ver los objetos en memoria (workspace)

ls()

1. 'a'
2. 'A'
3. 'fruta'
4. 'i'
5. 'I3'
6. 'Lst'
7. 'StdErr'
8. 'x'
9. 'y'

Borremos los objetos x, y.

rm(x,y)
ls()

1. 'a'
2. 'A'
3. 'fruta'
4. 'i'
5. 'I3'
6. 'Lst'
7. 'StdErr'

Borremos ahora todos los objetos.

rm(list=ls())
ls()

Creemos el vector x con los números de 1 a 20 y calculemos \( w = 1 + \frac{\sqrt{x}}{2} \). Mostremos además el data.frame con las dos columnas.

x <- 1:20
w <- 1 + sqrt(x)/2
y <- x + rnorm(x)*w
datos <- data.frame(x,y)
datos

A data.frame: 20 × 2

x	y
<int>	<dbl>
1	1.5487498
2	3.5900364
3	-0.5580842
4	4.1039770
5	3.2028486
6	5.1809214
7	8.4510867
8	10.9459662
9	3.4005430
10	9.0483977
11	10.7684991
12	15.6663345
13	17.7481259
14	15.8646092
15	16.0752924
16	15.0748889
17	18.5753744
18	15.1873128
19	19.6220873
20	19.4908391

Hay muchas funciones estadísticas descriptivas para obtener información de una base de datos, una función bastante completa es la función summary.

Nombre Comando	Explicación
summary(data)	Resumen estadístico
min(data)	Mínimo
max(data)	Máximo
range(data)	Rango
mean(data)	Media aritmética

summary(datos)

       x               y          
 Min.   : 1.00   Min.   :-0.5581  
 1st Qu.: 5.75   1st Qu.: 3.9755  
 Median :10.50   Median :10.8572  
 Mean   :10.50   Mean   :10.6494  
 3rd Qu.:15.25   3rd Qu.:15.9173  
 Max.   :20.00   Max.   :19.6221  

Podemos realizar gráficos y pruebas de hipótesis sobre las variable y, por ejemplo, podemos realizar un histograma o la prueba de normalidad Shapiro-Wilk donde \(H_0\) = La variable proviene de una distribución normal, \(H_1\) = La variable no proviene de una distribución normal. Vemos que p > 0.05, por lo tanto, no se rechaza la hipótesis nula y se asume que los datos provienen de una distribución normal.

hist(y)

shapiro.test(y) 

	Shapiro-Wilk normality test

data:  y
W = 0.9145, p-value = 0.0777

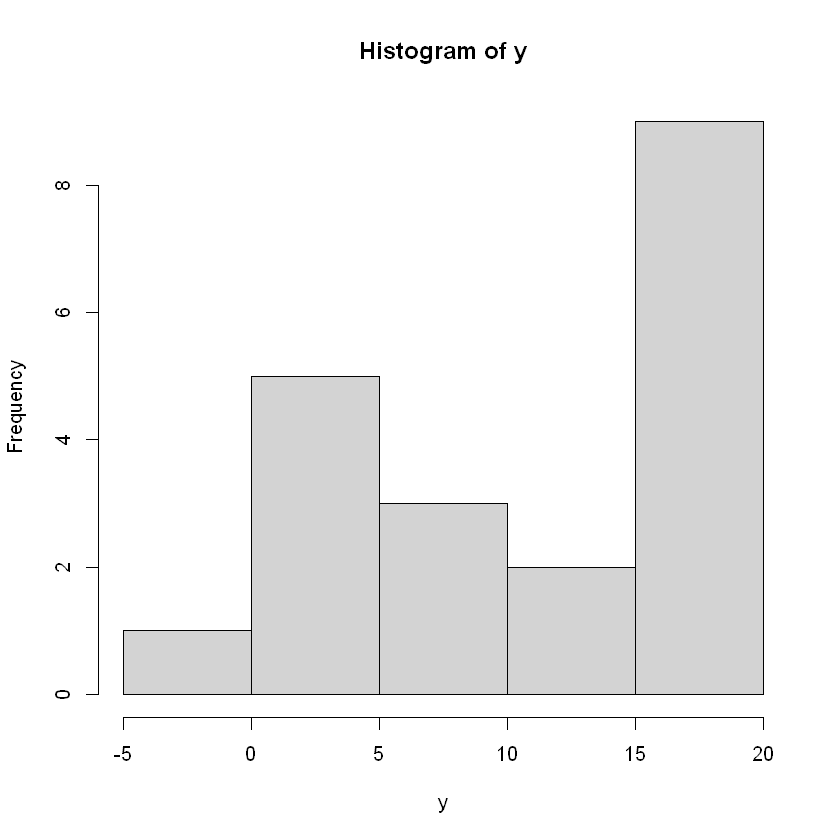
Realizamos el ajuste de un modelo de regresión lineal tomando y como respuesta y x como variable explicativa. Se presenta en pantalla un resumen del análisis.

regr <- lm(y ∼ x, data=datos)
summary(regr)

Error in parse(text = x, srcfile = src): <text>:1:14: unexpected input
1: regr <- lm(y ∼
                 ^
Traceback:

Puesto que se conocen las desviaciones típicas, puede realizarse una regresión ponderada.

regr.pon <- lm(y ∼ x, data=datos, weight=1/w^2)
summary(regr.pon)

Call:
lm(formula = y ~ x, data = datos, weights = 1/w^2)

Weighted Residuals:
     Min       1Q   Median       3Q      Max 
-2.27667 -0.42625  0.07218  0.56163  1.59884 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.30086    0.92395  -0.326    0.748    
x            1.04368    0.09421  11.078 1.81e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.021 on 18 degrees of freedom
Multiple R-squared:  0.8721,	Adjusted R-squared:  0.865 
F-statistic: 122.7 on 1 and 18 DF,  p-value: 1.807e-09

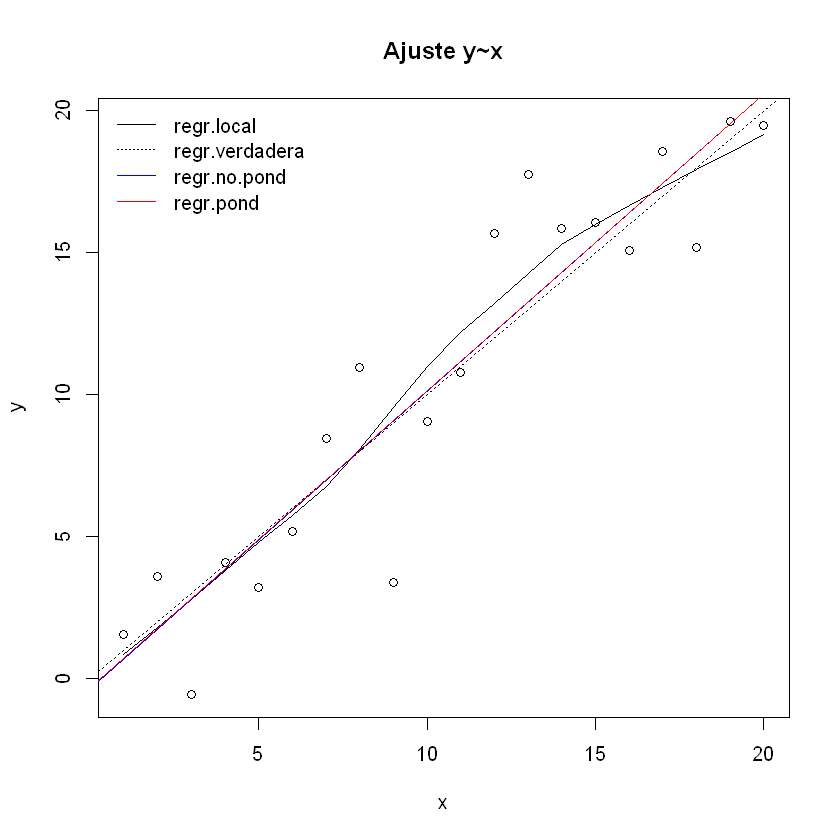
Para conectar o fijar los datos de tal modo que sus columnas aparecen como variables. Realizamos una regresión local no paramétrica.

attach(datos) #fijar los datos
regr.loc <- lowess(x, y) #regresión no paramétrica
plot(x, y, main="Ajuste y~x") #gráfico bidimensional estándar
lines(x, regr.loc$y) #regresión local
abline(0, 1, lty=3) #verdadera recta de regresión (punto de corte 0, pendiente 1)
abline(coef(regr), col="blue") #recta de regresión no ponderada
abline(coef(regr.pon), col="red") #recta de regresión ponderada
legend("topleft",
       legend = c("regr.local","regr.verdadera","regr.no.pond","regr.pond"),
       lty=c(1,3,1,1),
       col=c(1,1,4,2),
       bty = "n")
detach() #desconecta la hoja de datos

The following objects are masked _by_ .GlobalEnv:

    x, y

Un gráfico diagnóstico de regresión para investigar la posible heterocedasticidad (la varianza de los errores no es constante).

plot(fitted(regr), resid(regr),
     xlab="Predichos",
     ylab="Residuos",
     main="Residuos vs Predichos")

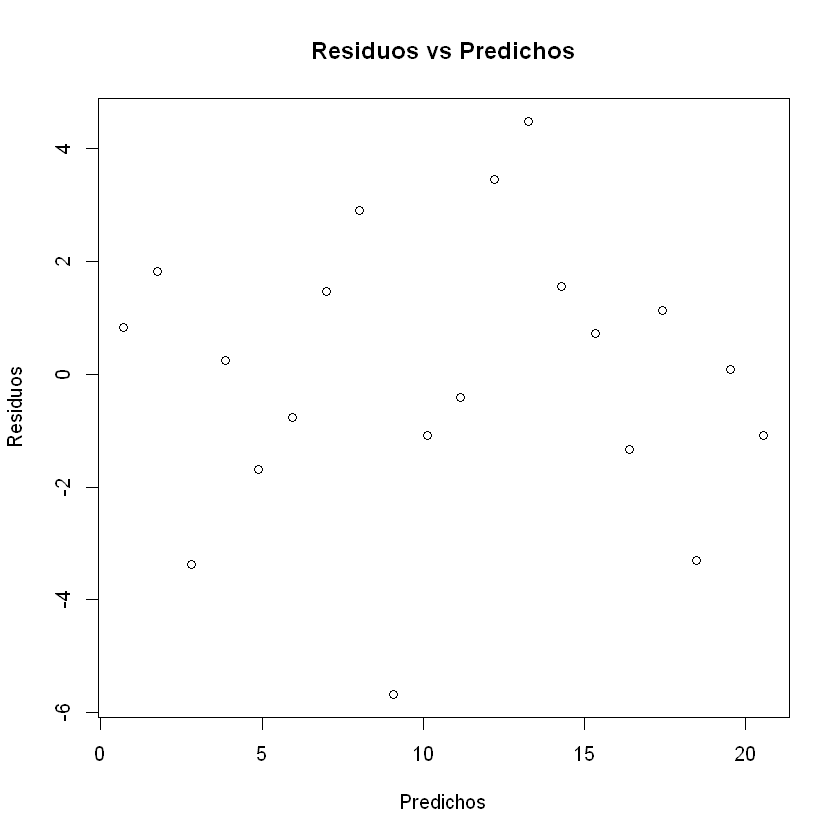
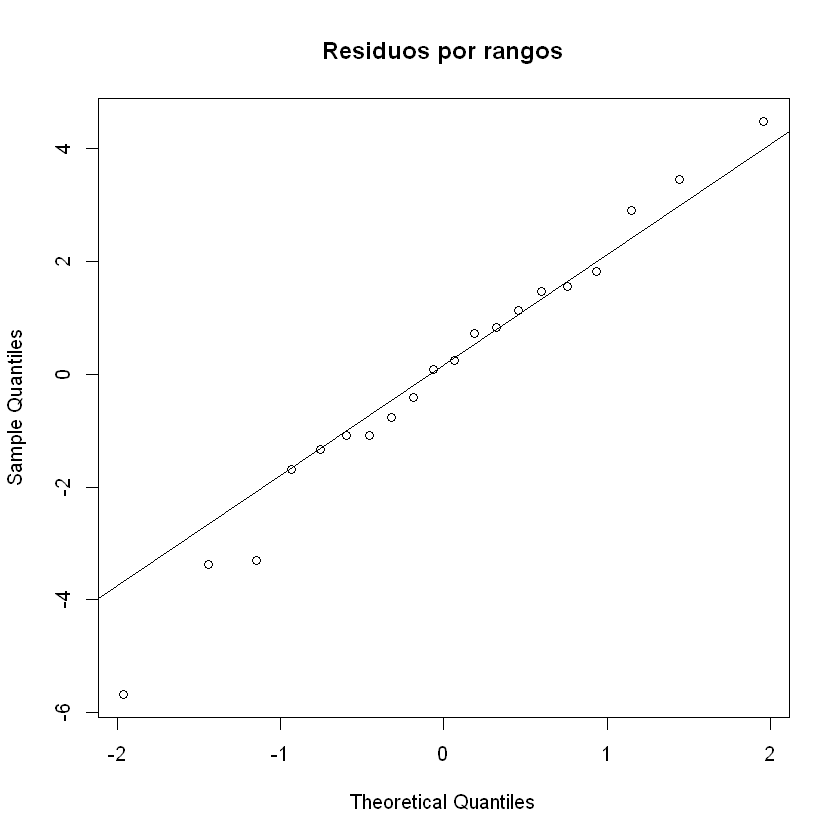
Podemos ver no hay heterocesdasticidad. Ahora, veamos a modo de introducción un gráfico en papel probabilístico normal para comprobar asimetría, aplastamiento y datos anómalos (No es muy útil en este caso).

qqnorm(resid(regr), main="Residuos por rangos")
qqline(resid(regr))
rm(x,w,datos,regr,regr.pon,regr.loc) #Elimina los objetos creados

Datos base

En R es posible leer datos en distintos formatos. En primera instancia se debe ubicar la carpeta donde se tienen los datos, luego se debe utilizar el código dependiendo del formato read.table, read_excel, read.csv, read.xlsx. En este caso vamos a trabajar con datos que se encuentran por defecto en R.

getwd() #se obtiene la ruta en la que se está ubicado actualmente
#setwd() #se cambia o se establece la ruta

'C:/Users/User/OneDrive/Documentos/Libro-Fundamentos-main/Machine_Learning/Cuadernos'

Vamos a utilizar los datos de Michaelson y Morley. Hay cinco experimentos (columna Expt) y cada uno contiene 20 series (columna Run) y la columna Speed contiene la velocidad de la luz medida en cada caso, codificada apropiadamente.

#data() #muestra todas las bases de datos incluidas base en R

data("morley") #carga la base de datos
head(morley)

	Expt	Run	Speed
001	1	1	850
002	1	2	740
003	1	3	900
004	1	4	1070
005	1	5	930
006	1	6	850

#Transforma Expt y Run en factores.
morley$Expt <- factor(morley$Expt)
morley$Run <- factor(morley$Run)

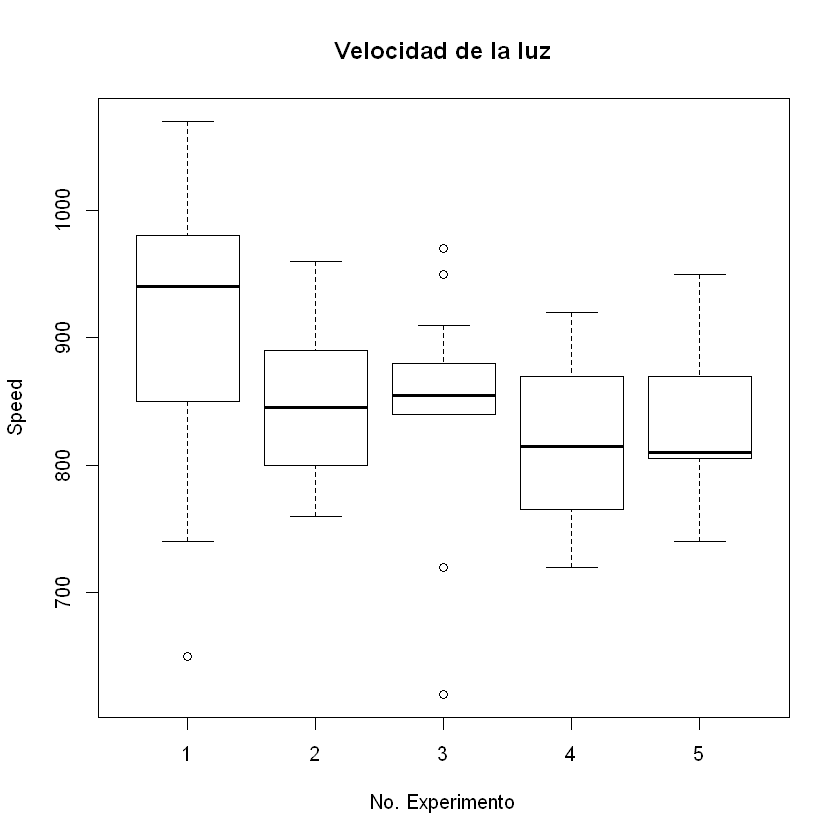
Comparamos los cinco experimentos mediante diagramas de cajas.

attach(morley)
boxplot(Speed~Expt, main="Velocidad de la luz", xlab="No. Experimento")

Instalación de paquetes

#install.packages("ggplot2")

# library
library(ggplot2)
 
# Top Left: Set a unique color with fill, colour, and alpha
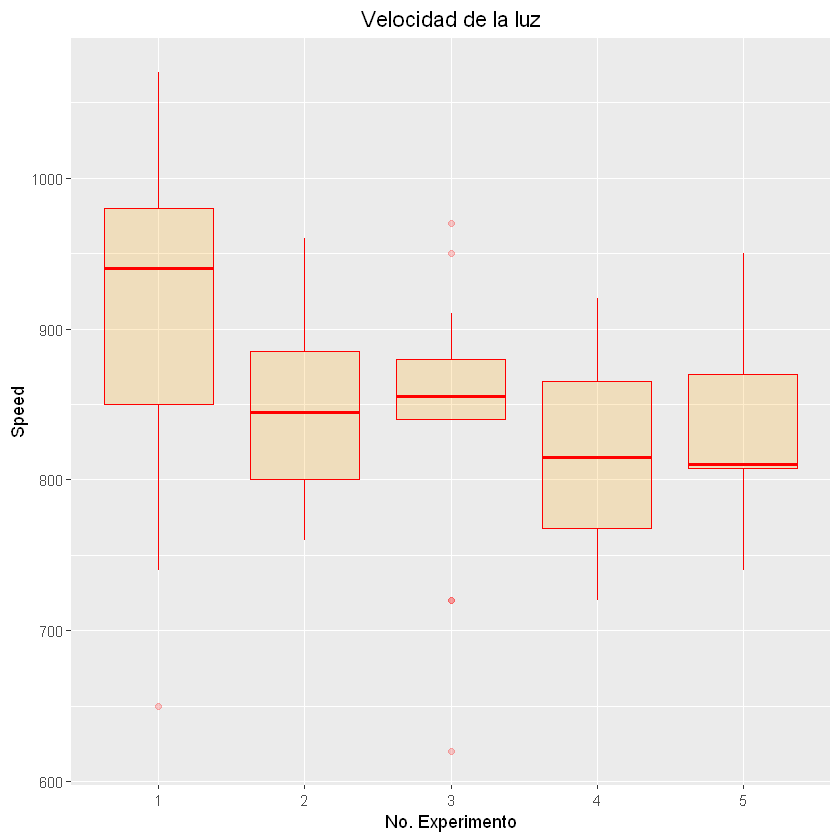
ggplot(morley, aes(x=Expt, y=Speed)) + 
    geom_boxplot(color="red", fill="orange", alpha=0.2) + 
    ggtitle("Velocidad de la luz") +
    xlab("No. Experimento") + 
    theme(plot.title = element_text(hjust = 0.5))

Registered S3 methods overwritten by 'ggplot2':
  method         from 
  [.quosures     rlang
  c.quosures     rlang
  print.quosures rlang

Analizamos los datos como un diseño en bloques aleatorizados, tomando las ‘series’ y los ‘experimentos’ como factores.

fm <- aov(Speed ∼ Run + Expt, data=morley) #Run 1:20, Expt 5
summary(fm)

            Df Sum Sq Mean Sq F value  Pr(>F)   
Run         19 113344    5965   1.105 0.36321   
Expt         4  94514   23629   4.378 0.00307 **
Residuals   76 410166    5397                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ajustamos un submodelo eliminando las ‘series’ para compararlos utilizando un análisis de la varianza. Podemos ver que el valor-P es > 0.05 y por lo tanto, los modelos no son significativamente distintos, y por lo tanto el efecto producido por el bloque Run no mejora el modelo.

fm0 <- update(fm, . ∼ . - Run)
anova(fm0,fm)
detach() #Desconecta la hoja de datos
rm(fm, fm0) #Elimina los objetos creados

Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
95	523510	NA	NA	NA	NA
76	410166	19	113344	1.105348	0.3632093

Algunos gráficos

Consideraremos ahora nuevas posibilidades gráficas.

x <- seq(-pi, pi, len=50) #x es un vector con 50 valores equiespaciados en el intervalo −π ≤ x ≤ π
y <- x #El vector y es idéntico a x.

f es una matriz cuadrada, cuyas filas y columnas están indexadas por x e y respectivamente, formada por los valores de la función \( cos(y)/(1 + x2) \).

f <- outer(x, y, function(x, y) cos(y)/(1 + x^2)) #almacenamos los parámetros gráficos

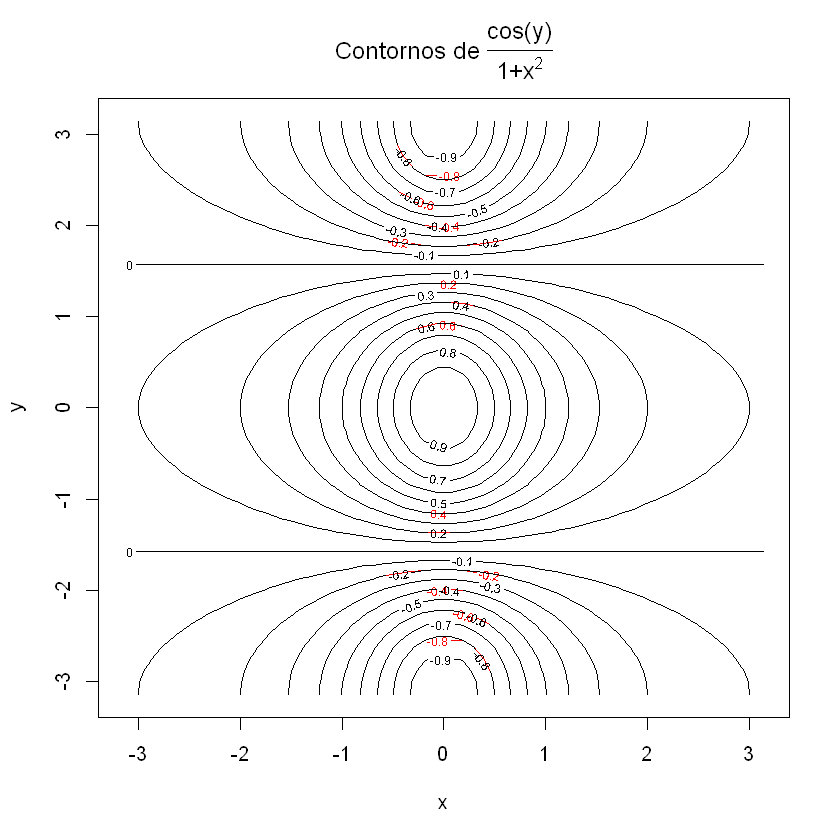
Dibujamos un mapa de curvas de nivel de f y después le añadimos más líneas para obtener más detalle.

contour(x, y, f, col=2, main=expression(paste("Contornos de ",frac("cos(y)", "1+x"^2),sep='')), xlab="x", ylab="y")
contour(x, y, f, nlevels=15, add=TRUE)

Dibujamos un gráfico de densidad.

image(x, y, f)

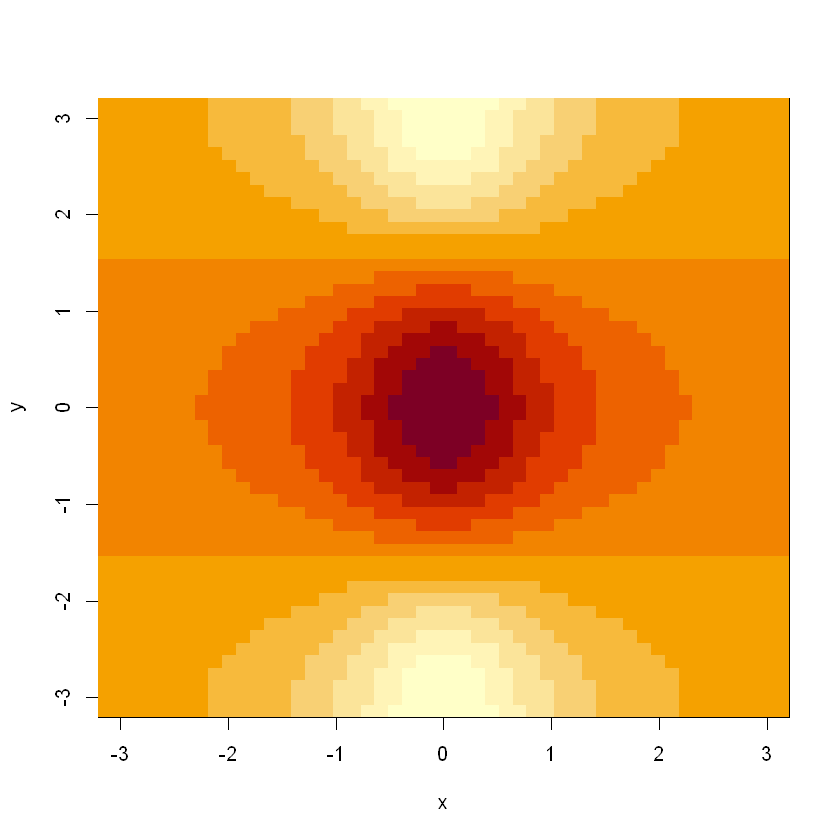
Presenta los objetos existentes y elimina los objetos creados, antes de seguir adelante. Con R también se puede utilizar números complejos. 1i se utiliza para representar la unidad imaginaria, i.

ecuacion <- expression(f == frac(cos(y), 1+x^2))
persp(x, y, f, theta = 30, phi = 30, expand=0.5, col = "darkgreen",
      main="Gráfico 3D usando la función persp", sub=ecuacion, col.main="blue")

objects(); rm(x, y, f)

1. 'ecuacion'
2. 'f'
3. 'morley'
4. 'x'
5. 'y'

La representación gráfica de un argumento complejo consiste en dibujar la parte imaginaria frente a la real. En este caso se obtiene un círculo. Ademas con la función par y el argumento pty vamos a cambiar el tipo de región de dibujo, «s» genera una región de gráficos cuadrada y «m» genera la región de dibujo máxima.

th <- seq(-pi, pi, len=100)
z <- exp(1i*th)
par(pty="s")
plot(z, type="l")

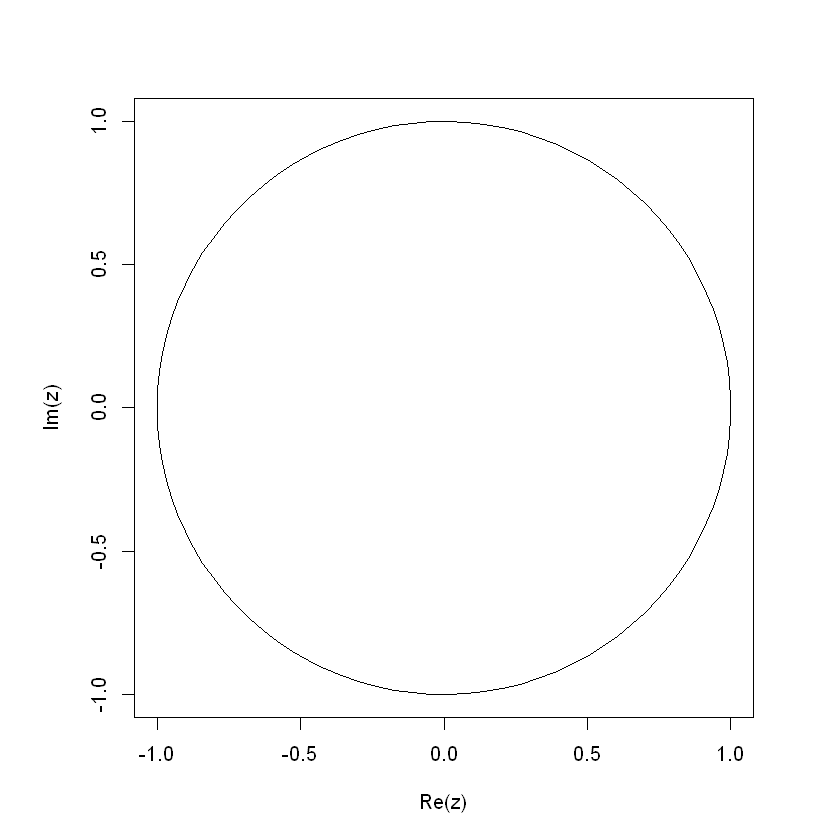
Suponga que desea generar puntos pseudoaleatorios dentro del círculo unidad. Un primer intento consiste en generar puntos complejos cuyas partes real e imaginaria, respectivamente, procedan de una N(0,1) y sustituir los que caen fuera del círculo por sus inversos.

w <- rnorm(100) + rnorm(100)*1i
w <- ifelse(Mod(w) > 1, 1/w, w)
par(pty="s")
plot(w, xlim=c(-1,1), ylim=c(-1,1), pch="+",xlab="x", ylab="y")
lines(z)
#Todos los puntos estan dentro del cırculo unidad, pero la distribucion no es uniforme.

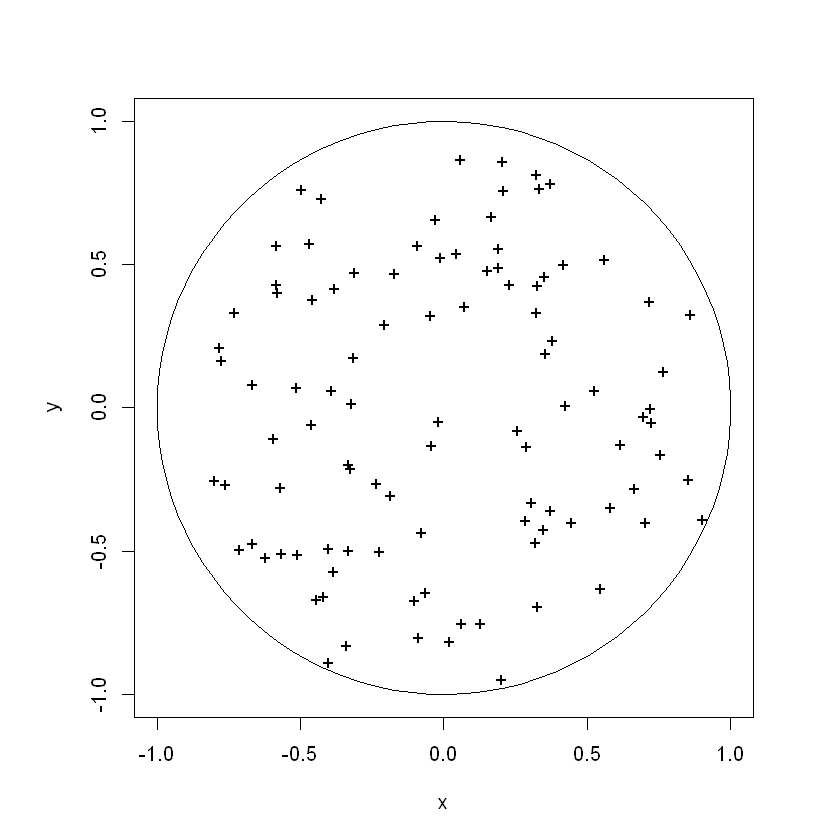
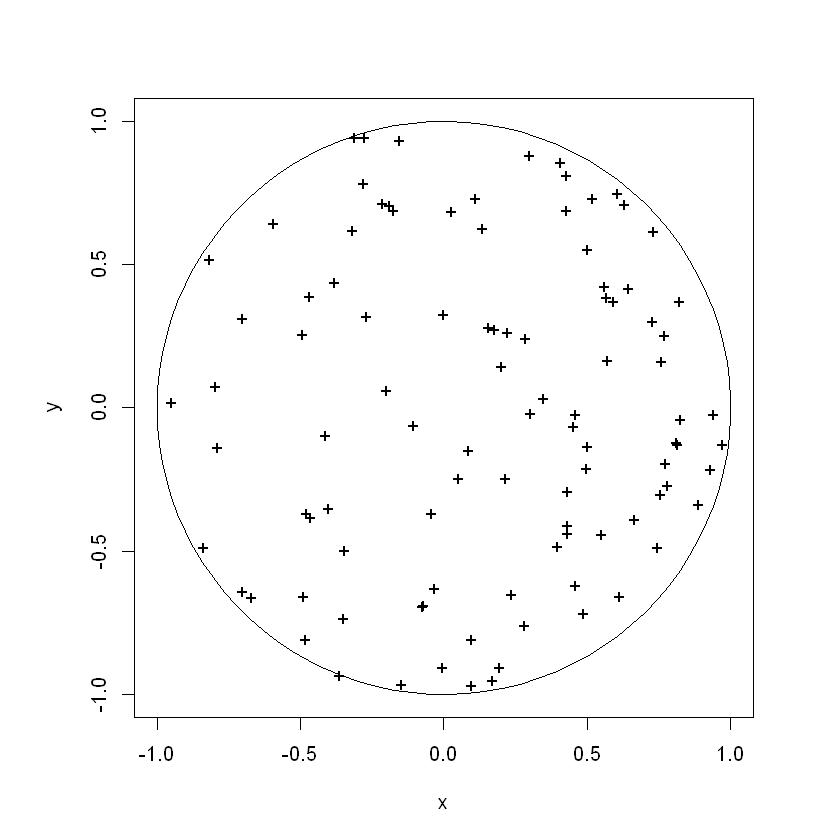
Este segundo método utiliza la distribución uniforme. En este caso, los puntos presentan una apariencia más uniformemente espaciada sobre el círculo.

w <- sqrt(runif(100))*exp(2*pi*runif(100)*1i)
par(pty="s")
plot(w, xlim=c(-1,1), ylim=c(-1,1), pch="+", xlab="x", ylab="y")
lines(z)

Algunos aspectos claves y herramientas cotidianas

• R considera diferencias entre mayúsculas y minúsculas.

• Los comentarios en R empiezan con # y van en cualquier parte de la linea siempre que no interrumpan la lógica de una instrucción.

• El salto de linea y el punto y coma son los separadores de comandos.

• Para definir o asignar un objeto se una <-, -> o =

• En la consola de R con las flechas hacia arriba y hacia abajo se navega por los comandos ya utilizados.

• La estructura más pequeña de R es un vector. Entonces un escalar es un vector.

• Hay que entender las clases y las funciones genéricas de R.

  • Las funciones se programan para diferentes objetos y R las selecciona de acuerdo al objeto de entrada.

  • Las funciones reciben parámetros de ciertas clases y si los utilizados al llamarlas no corresponden, se ocasiona un error.

  • Las funciones de R tienen argumentos por defecto, los que se pueden cambiar al momento de llamarlas (utilizarlas).

Adicional (Aprende R, en R.)

Swirl, es un paquete que permite aprender de forma interactiva directamente en R, cuenta con diversos cursos para principiantes, intermedios y avanzados, puede usarse en la consola aunque recomiendan utilizar RStudio.

• install.packages(«swirl») —–>Instala

• library(«swirl») —–>se llama la librería

• swirl() —–>se inicia los cursos base

• bye() —–>se cierran los cursos

Referencias

• R para principiantes

• Introducción a R