Aprendizaje no supervisado
Contents
Aprendizaje no supervisado#
Nota
Los trozos de código de esta página son de R. Por favor, ejecútelos en Colab o Binder
Introducción#
En el aprendizaje no supervisado se tienen tablas de datos donde no hay una variable de respuesta. Lo que se busca es «entender» los datos, buscar patrones de comportamiento en ellos, describir y explorar lo que está oculto. En el aprendizaje se mencionan como técnicas de visualización. En Estadística se habla de un área de ella, la descriptiva: univariada, bivariada y multivarida. Los índices estadísticos complementan a los gráficos. Los gráficos son más fáciles de comprender por nuestro cerebro y esa es la razón de que se busquen representaciones y resúmenes gráficos.
Para entender la información que emerge de los datos, es necesario conocer el contexto del entorno del que los datos forman parte: metainformación. La metainformación más próxima a los datos puestos en una tabla, está en los nombres de las filas y columnas. En las filas generalmente, se ponen las unidades estadísticas, claramente definidas en el estudio que está desarrollando. Usamos el nombre genérico de individuos para esas unidades estadísticas. En los datos más estructurados, las columnas suelen ser las variables o características que queremos observar.
Visualizar, entender, describir, explorar los datos, es también útil, antes de abordar modelos de aprendizaje supervisado. Entender la realidad a través de los datos ayuda a selecciones mejor los modelos y podrían ayudar a llegar a los modelos adecuados de forma más rápida.
Las tablas de datos de individuos por variables continuas se conocen como matrices en el Álgebra lineal, el área de las matemáticas que nos sirve para ver las tablas como puntos en es representaciones geométricas multidimensionales. En lugar de tratar de entender la tabla de datos (digital) observamos su representación gráfica (analógica).
Se suelen utilizar letras mayúsculas para representar a las matrices. Las tablas de individuos, usaremos n para indicar el número de filas (individuos) y p para el número de variables. Si denotamos por Y la matriz, tiene dimensiones n por p, es decir n individuos. Se suelen utilizar los subíndices i y j para recorrer filas y columnas.

Fuente: Medium
La representación de una matriz de números reales (variables continuas) y su visualización mediante proyecciones da origen al método de análisis en componentes principales. Esta representación hace uso de una parte del Álgebra lineal, que se puede denominar: espacios vectoriales con producto interno. El producto interno que se define haciendo uso de una matriz cuadrada, simétrica y definida positiva, por las condiciones que debe cumplir. La más sencilla es la matriz identidad, como es cuadrada, el número de filas es igual al número de columnas, y es el orden de la matriz.
La geometría de nuestra vida diaria está en 3 dimensiones y la matriz que define el producto interno es I\(_3\):
I=diag(3); I
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
De la matriz de métrica se derivan: normas, distancias, proyecciones, ángulos. Para la matriz Y se tienen dos representaciones que denominamos nubes de puntos y denotamos por N con un subíndice para tener el número de puntos que hay en la nube. Para la tabla Y (\(n\times p\)) tenemos la nube de filas o individuos N\(_n\), en \(\mathbb{R}^p\) y la nube de columnas o variables N\(_p\), en \(\mathbb{R}^n\). Para que los vectores de la representación geométrica de las variables muestren los resúmenes estadísticos de las variables, el espacio vectorial \(\mathbb{R}^n\) denota la métrica \(\frac{1}{n}\mathbf{I}\). Por ejemplo, si \(n=5\) es \(\frac{1}{5}\mathbf{I}\):
1/5*diag(5)
| 0.2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.2 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.2 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.2 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.2 |
La generalización del ACP, utilizando otras métricas y transformando previamente las tablas que se desean explorar, permite tener imágenes geométricas para: tablas de contingencia, frecuencias y otras de números positivos (Análisis de correspondencias simples); y para tablas de individuos por variables cualitativas (Análisis de correspondencias múltiples). A continuación se muestras un esquema de esos tres métodos factoriales o en ejes principales:

Lo que muestra la figura es la proyección de nubes de puntos que están en muchas dimensiones en planos. Si partimos de un espacio de 100 dimensiones podemos hacer una primera lectura en el mejor plano, es decir en el que menos se deforman las longitudes o normas de los vectores, que equivale a que se pierde menos de las longitudes de los vectores. Seguramente un plano no es suficiente y hay que decidir cuál es la dimensión del subespacio S que se va a observar. Si decidimos observar en \(S=5\) dimensiones es subespacio es \(\mathbb{R}^5\) y tampoco lo puedo ver y tendríamos que leer varios planos. El primero formado por los nuevos ejes 1 y 2 es el mejor plano y en principio debería observar las 10 parejas de planos.
Otra manera de resumir la información es hacer una partición: grupos o clases disyuntos y cuya unión es el conjunto de todos los datos. Aquí aprovechamos las representaciones geométricas de los métodos factoriales. Entonces se trata de buscar grupos geométricamente, los métodos que se asocian a esa búsqueda son el \(K{-}means\), algoritmo que busca una partición directa. Tiene ventajas pero tiene dos problemas: hay que darle al algoritmo el número de clases K y ese número que queremos decidir a partir de la estructura de los datos; y generalmente converge a un óptimo local y no global, es decir que la partición en \(K\) clases depende de los puntos iniciales. Entonces se usa el método de Ward, de clasificación ascendente jerárquica aglomerativa, como una manera de solucionar esos dos problemas. Estos métodos se tratan de clasificación no supervisada o agrupamiento, en inglés se conocen como Cluster Analysis. Los algoritmos de clasificación ascendente jerárquica aglomerativa parte de los n individuos, se unen los dos más cercanos para formar un grupo y se tiene una partición de \(n-1\) grupos: uno de dos individuos y \(n-2\) de uno. El grupo formado pasa a jugar el papel de un individuo, de modo que se sigue el procedimiento hasta llegar a un solo grupos de \(n\) individuos. Este proceso se puede ver como un árbol y de su observación podemos decidir sobre una o más particiones. Una partición se obtiene al cortar el árbol lo que origina K ramas separadas, que corresponden a las clases. Los dos problemas de este segundo tipo de métodos son: su consumo de recursos de cómputo y la restricción de anidamiento de las particiones. En la figura se muestra un árbol pequeño.
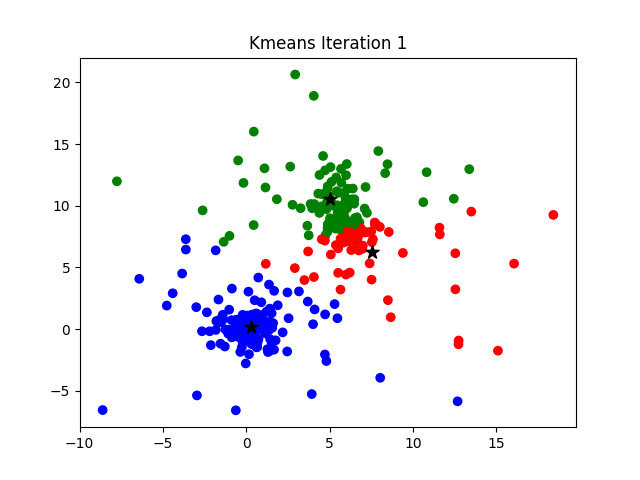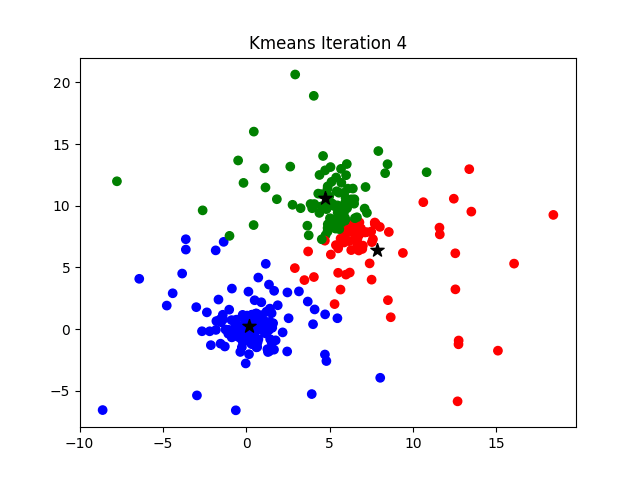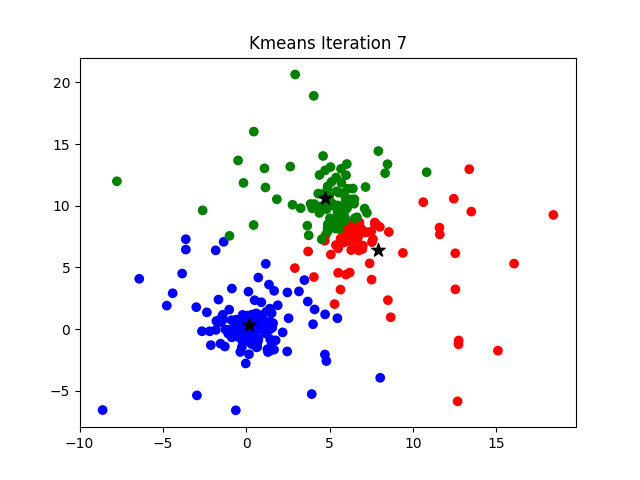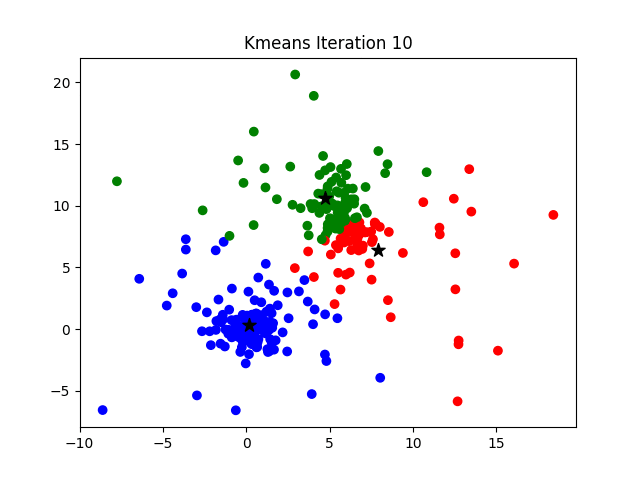
FuenteMedium
Cuando el número de individuos es muy grande, se realiza \(K{-}means\) para obtener una partición en miles de clases, que entrarán al método de Ward. Para el segundo problema se realiza una optimización o consolidación de la partición obtenida con el \(K{-}means\). Nótese que el método de Ward provee una manera de solucionar los dos problemas del \(K{-}means\): provee el número K de clases y los puntos iniciales. A su vez el \(K{-}means\) provee una solución a los problemas del método de Ward: la saturación del sistema de cómputo y la restricción de anidamiento de la partición.
data(iris)
hcl <- hclust(dist(iris[,-5]),method="ward.D2")
barplot(hcl$height[149:130],horiz=TRUE)
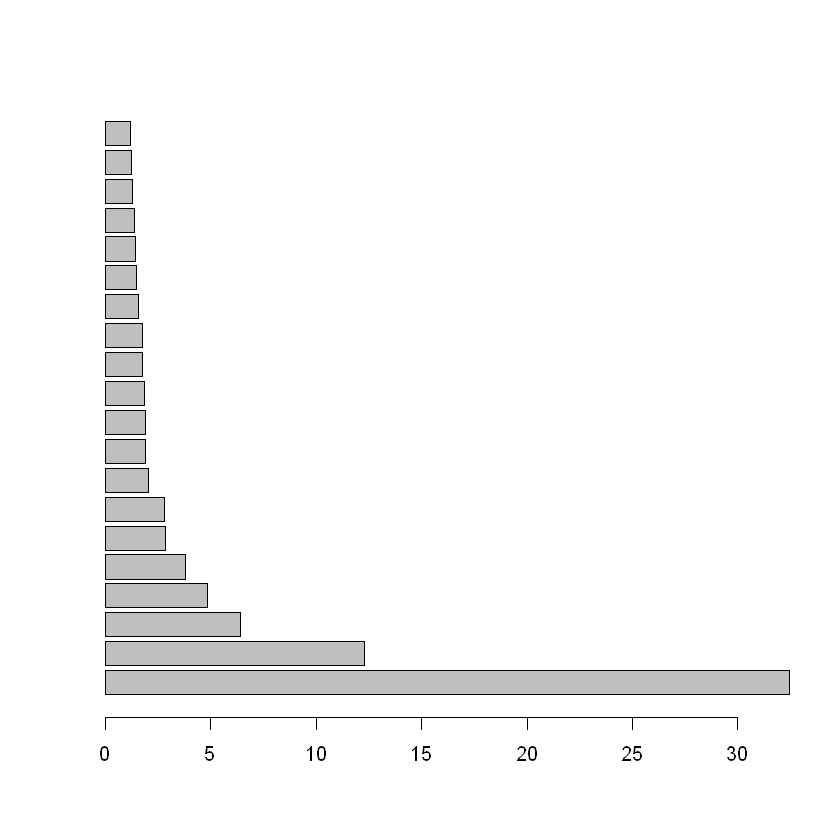
plot(hcl)
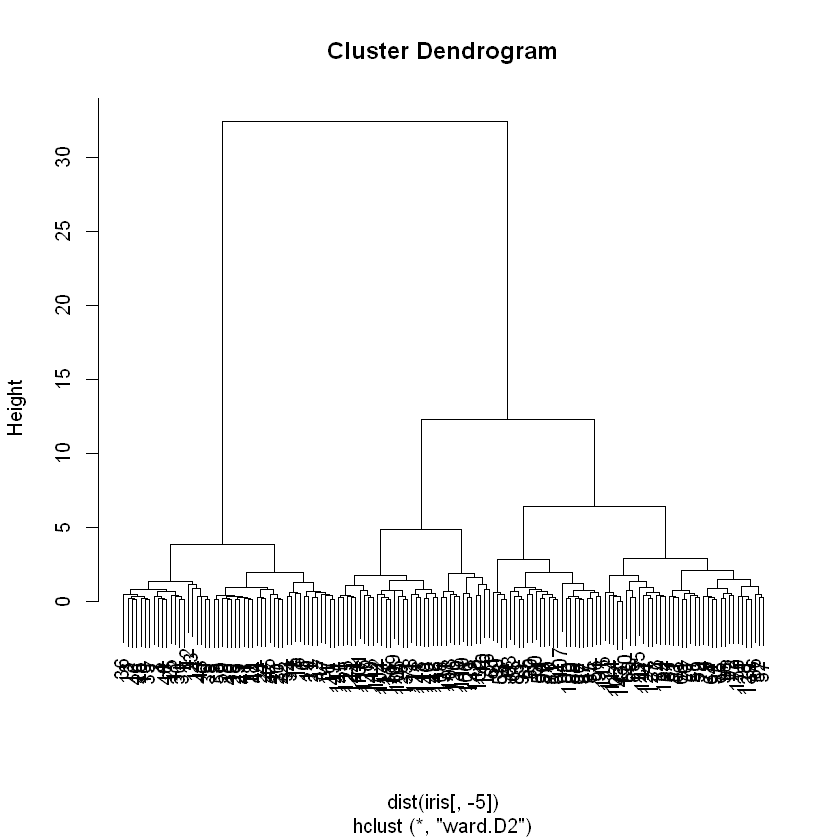
En el libro Estadística descriptiva multivariada, se explican estos métodos. Se puede bajar de la página de la Facultad de Ciencias, en este link.
Descripción bivariada simultánea#
Estoy llamando Descripción univariada simultánea cuando observamos a la vez las descripciones bivariadas da varias parejas de variables. Para hacerlo las variables según las escalas de medida se dividen solo en dos tipos: cualitativas (nominales e ordinales) y continuas (de intervalo de razón). Entonces, se tienen tres tipos de parejas de variables:
Dos continuas.
Una cualitativa y una continua.
Dos cualitativas.
En estas descripciones se privilegian las descripciones gráficas.
Descripción bivariada de varias parejas de variables continuas#
En FactoClass hemos programado la función plotpairs que enriquece la función pairs de R, dejando los diagramas de dispersión en la parte triangular inferior del panel de gráficas, en la parte triangular superior se grafican curvas de nivel de densidades kernel bivariadas, y el panel de la diagonal se utiliza para dibujar las densidades kernel de las marginales.
Vamos a utilizarla para ver las seis parejas de las cuatro variables. En el Colab no está disponible el paquete FactoClass, por lo tanto tenemos que instalarlo:
#install.packages("FactoClass")
Para hacer disponibles sus funciones hay que cargarla:
library(FactoClass)
Loading required package: ade4
Loading required package: ggplot2
Loading required package: ggrepel
Loading required package: xtable
Loading required package: scatterplot3d
Ahora sí la gráfica:
data(iris)
plotpairs(iris[,1:4])
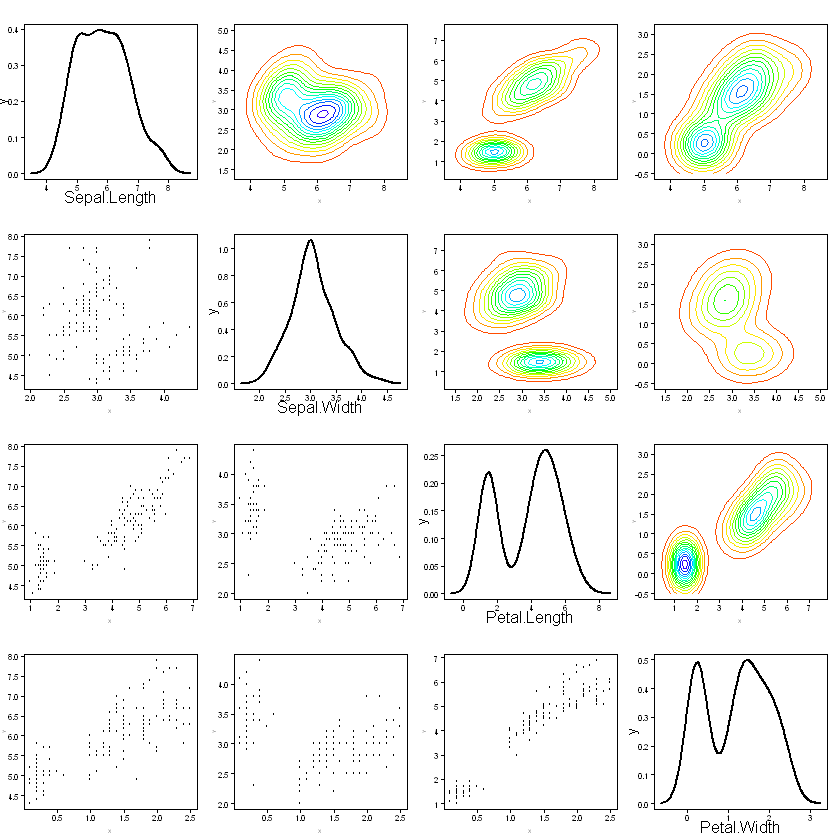
En este panel de gráficas podemos explorar la existencia de grupos. Vemos claramente dos grupos en todos los diagramas de dispersión y una separaciones claras, en los contornos de las densidades kernel, cuando una de las variables es la longitud del pétalo. Las variables longitud y ancho del pétalo son las que mejor separan entre los dos grupos.
En el ejemplo iris se conocen que las flores son de tres especies y podemos explorar su separación identificando la pertenencia a las clases con símbolos y colores. La función plomatrix del paquete amun programado por tres estudiantes de algún curso Análisis multivariado de la Carrera de Estadística, lo hace. Sin embargo no está en el CRAN y la voy a utilizar desde mi consola de R:
Ejecutar desde consola
Las gráficas se pueden complementar con las matriz de varianzas y covarianzas; y la de correlaciones:
round(var(iris[,-5]),2)
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | |
|---|---|---|---|---|
| Sepal.Length | 0.69 | -0.04 | 1.27 | 0.52 |
| Sepal.Width | -0.04 | 0.19 | -0.33 | -0.12 |
| Petal.Length | 1.27 | -0.33 | 3.12 | 1.30 |
| Petal.Width | 0.52 | -0.12 | 1.30 | 0.58 |
as.dist(round(cor(iris[,-5]),2))
Sepal.Length Sepal.Width Petal.Length
Sepal.Width -0.12
Petal.Length 0.87 -0.43
Petal.Width 0.82 -0.37 0.96
Descripción bivariada de una variable cualitativa y varias continuas#
Una variable cualitativa representa una partición del conjunto de individuos. Un boxplot puede comparar los grupos según una variable cualitativa. En el ejemplo iris veamos los boxplot de las tres especies para la longitud del pétalo.
boxplot(iris[,3]~iris[,5])
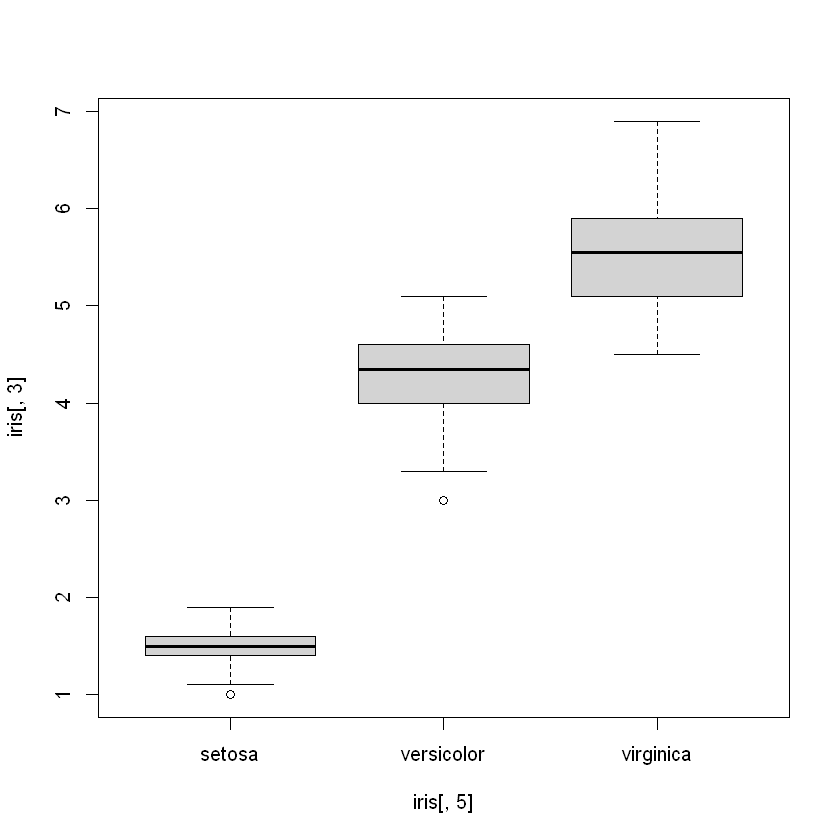
La asociación de una variable cualitativa y otra continua se puede resumir con la razón de correlación, definida como varianza entre grupos sobre varianza total (ver en el libro). Con la función centroids{FactoClass} calculan las medias y las razones de correlación de las tres especies.
centroids(iris[,-5],iris[,5])
- $centroids
A matrix: 3 × 4 of type dbl Sepal.Length Sepal.Width Petal.Length Petal.Width setosa 5.006 3.428 1.462 0.246 versicolor 5.936 2.770 4.260 1.326 virginica 6.588 2.974 5.552 2.026 - $weights
- setosa
- 0.333333333333333
- versicolor
- 0.333333333333333
- virginica
- 0.333333333333333
- $cr
A matrix: 1 × 4 of type dbl Sepal.Length Sepal.Width Petal.Length Petal.Width 0.6187057 0.4007828 0.9413717 0.9288829
Finalmente con la función cluster.carac{FactoClass) se pueden observar las variables que más caracterizan a cada una de las tres especies.
cluster.carac(iris[,-5],iris[,5],tipo.v="co")
class: setosa
Test.Value Class.Mean Frequency Global.Mean
Sepal.Width 7.365 3.428 50 3.057
Sepal.Length -8.757 5.006 50 5.843
Petal.Width -10.831 0.246 50 1.199
Petal.Length -11.264 1.462 50 3.758
------------------------------------------------------------
class: versicolor
Test.Value Class.Mean Frequency Global.Mean
Petal.Length 2.463 4.26 50 3.758
Sepal.Width -5.709 2.77 50 3.057
------------------------------------------------------------
class: virginica
Test.Value Class.Mean Frequency Global.Mean
Petal.Width 9.392 2.026 50 1.199
Petal.Length 8.801 5.552 50 3.758
Sepal.Length 7.788 6.588 50 5.843
Descripción bivariada de una variable cualitativa por varias nominales#
La asociación entre dos variables cualitativas se puede observar gráficamente con los perfiles fila y columna, derivados de la tabla de contingencia. Podemos utilizar el ejemplo del libro para observar la asociación entre las carreras y la edad. La función plotct{FactoClass} permite hacerlo:
data(admi)
names(admi)
K<-unclass(table(admi$carr,admi$edad)) # tabla de contingencia como matriz
addmargins(K)
- 'carr'
- 'mate'
- 'cien'
- 'soci'
- 'text'
- 'imag'
- 'exam'
- 'gene'
- 'estr'
- 'orig'
- 'edad'
- 'niLE'
- 'niMa'
- 'stra'
- 'age'
| a16m | a17 | a18 | a19M | Sum | |
|---|---|---|---|---|---|
| Biol | 15 | 27 | 9 | 12 | 63 |
| Esta | 18 | 28 | 5 | 15 | 66 |
| Farm | 18 | 26 | 15 | 14 | 73 |
| Fisi | 21 | 34 | 12 | 15 | 82 |
| Geol | 11 | 25 | 2 | 7 | 45 |
| Mate | 11 | 14 | 5 | 23 | 53 |
| Quim | 24 | 17 | 8 | 14 | 63 |
| Sum | 118 | 171 | 56 | 100 | 445 |
plotct(K,"row",col=c("darkgreen","green","yellow","orange"))
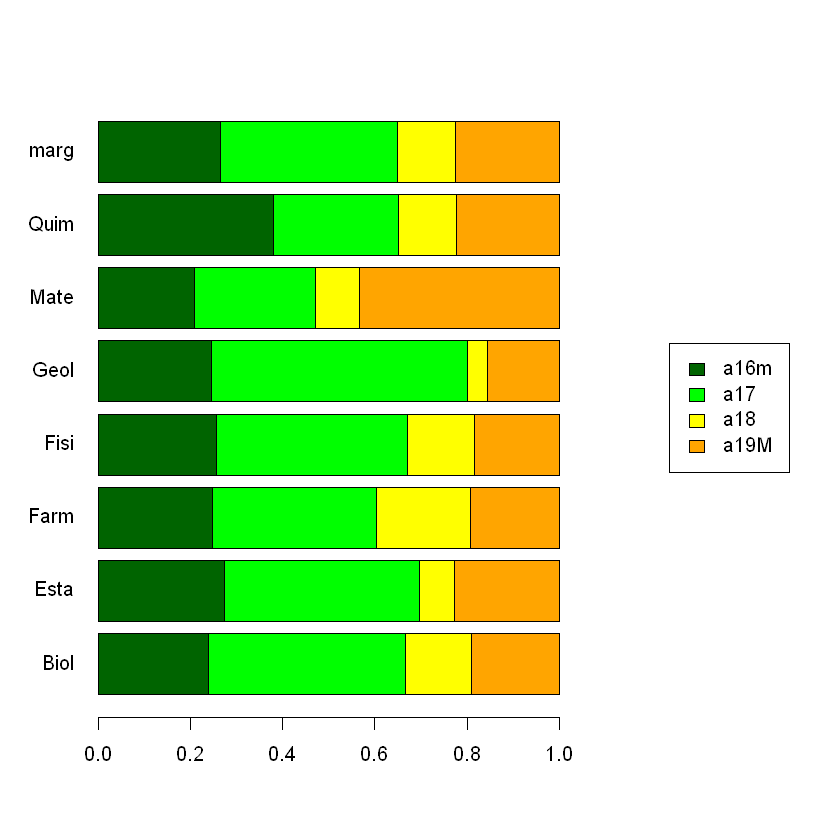
plotct(K,"col",col=1:7)
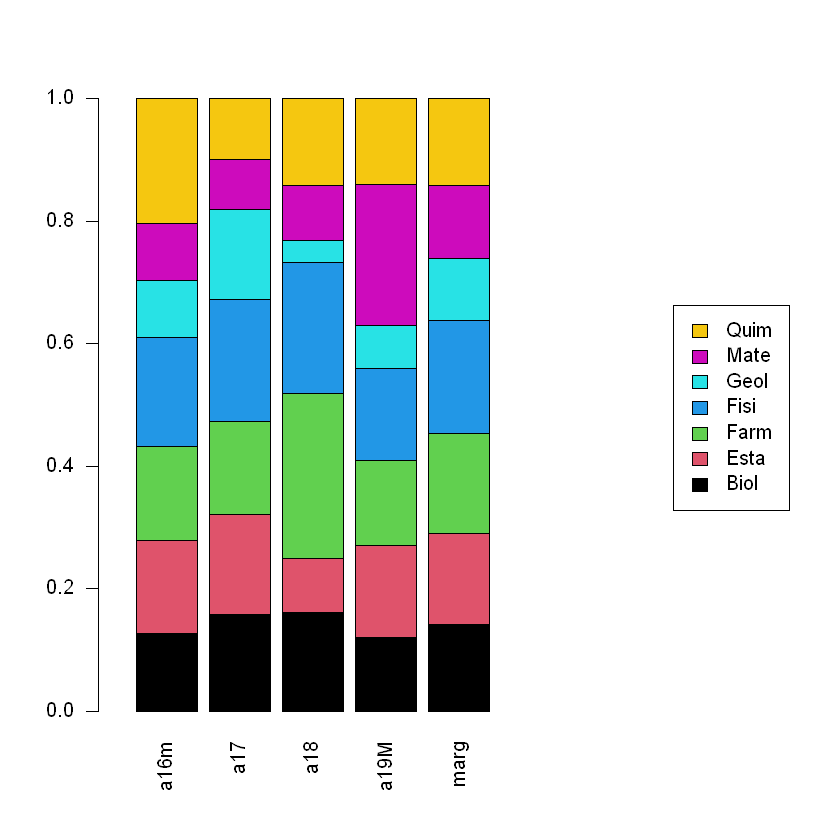
Para ordenar por las variables sociodemográficas que más caraterizan a las carreras.
chisq.carac(admi[,8:11],admi[,1])
| chi2 | dfr | pval | tval | phi2 | |
|---|---|---|---|---|---|
| gene | 44.10803 | 6 | 7.036257e-08 | 5.264299 | 0.09911918 |
| estr | 29.19000 | 12 | 3.691872e-03 | 2.679022 | 0.06559551 |
| edad | 33.55344 | 18 | 1.429273e-02 | 2.189157 | 0.07540098 |
Finalmente para ordenar por las categorías de las variables sociodemográficas que más caracterizan a las carrera.
cluster.carac(admi[,8:11],admi[,1],tipo.v="nomi")
class: Biol
[1] Test.Value p.Value Class.Cat Cat.Class Global Weight
<0 rows> (or 0-length row.names)
------------------------------------------------------------
class: Esta
[1] Test.Value p.Value Class.Cat Cat.Class Global Weight
<0 rows> (or 0-length row.names)
------------------------------------------------------------
class: Farm
Test.Value p.Value Class.Cat Cat.Class Global Weight
gene.F 5.152 0.000 31.2 54.8 28.8 128
edad.a18 2.252 0.024 26.8 20.5 12.6 56
estr.alto -2.281 0.023 8.6 9.6 18.2 81
gene.M -5.152 0.000 10.4 45.2 71.2 317
------------------------------------------------------------
class: Fisi
Test.Value p.Value Class.Cat Cat.Class Global Weight
gene.M 3.045 0.002 21.8 84.1 71.2 317
gene.F -3.045 0.002 10.2 15.9 28.8 128
------------------------------------------------------------
class: Geol
Test.Value p.Value Class.Cat Cat.Class Global Weight
estr.alto 3.677 0.000 22.2 40.0 18.2 81
edad.a17 2.554 0.011 14.6 55.6 38.4 171
estr.medio -3.242 0.001 4.9 20.0 41.6 185
------------------------------------------------------------
class: Mate
Test.Value p.Value Class.Cat Cat.Class Global Weight
edad.a19M 3.683 0.000 23.0 43.4 22.5 100
gene.M 3.218 0.001 14.8 88.7 71.2 317
edad.a17 -2.089 0.037 8.2 26.4 38.4 171
gene.F -3.218 0.001 4.7 11.3 28.8 128
------------------------------------------------------------
class: Quim
Test.Value p.Value Class.Cat Cat.Class Global Weight
edad.a16m 2.320 0.020 20.3 38.1 26.5 118
edad.a17 -2.189 0.029 9.9 27.0 38.4 171


