Análisis de correspondencias simples#

Nota

Los trozos de código de esta página son de R. Por favor, ejecútelos en Colab o Binder

Fuente: Pardo CE (2020) Estadística descriptiva multivariada

Objetivos de ACS#

Explorar y describir tablas de contingencia (TC), tablas de frecuencias y algunas tablas de números positivos.

Comparar los perfiles fila.
Comparar los perfiles columna.
Estudiar las correspondencias entre perfiles fila y columna.

Adicionalmente:

Cuantificación de las categorías fila y columna
Reducción de la dimensión
Filtro: separar información de ruido.

El ACS se puede ver como:

Dos ACP: uno de los perfiles fila y otro de perfiles columna, que se superponen.
Un ACP de los desvíos de la tabla de frecuencias relativas a la tabla del modelo de independencia.

Ejemplo «de juguete» y notación#

Ejemplo TC de los 445 admitidos: 7 carreras $\times$ 3 estratos.
La tabla de contingencia.

# carga de FactoClass y definición de Y
#install.packages('FactoClass')
library(FactoClass)

Loading required package: ade4

Loading required package: ggplot2

Loading required package: ggrepel

Loading required package: xtable

Loading required package: scatterplot3d

# Una idea de la estructura de los datos
data(admi)
str(admi)

'data.frame':	445 obs. of  15 variables:
 $ carr: Factor w/ 7 levels "Biol","Esta",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ mate: num  12 11.8 10 11.5 11.2 ...
 $ cien: num  10.8 11.2 10.5 11.5 10.8 ...
 $ soci: num  12.1 11.7 10.7 11.7 12.1 ...
 $ text: num  10.62 10.35 9.57 10.91 11.21 ...
 $ imag: num  10.7 11.6 8.8 11.6 11.3 ...
 $ exam: num  696 703 504 715 693 ...
 $ gene: Factor w/ 2 levels "F","M": 1 2 1 1 2 1 1 2 1 2 ...
 $ estr: Factor w/ 3 levels "bajo","medio",..: 3 2 1 1 2 2 2 2 2 2 ...
 $ orig: Factor w/ 3 levels "Bogo","Cund",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ edad: Factor w/ 4 levels "a16m","a17","a18",..: 2 2 3 3 2 2 2 2 4 3 ...
 $ niLE: Factor w/ 2 levels "siLE","noLE": 2 2 1 2 2 2 2 2 2 2 ...
 $ niMa: Factor w/ 2 levels "siMa","noMa": 1 1 1 1 1 1 1 1 2 2 ...
 $ stra: Factor w/ 7 levels "E0","E1","E2",..: 5 4 3 3 4 4 4 4 4 4 ...
 $ age : num  17 17 18 18 17 17 17 17 19 18 ...

Tabla de contingencia#

K<-unclass(table(admi$carr,admi$estr))
addmargins(K)

A matrix: 8 × 4 of type dbl
	bajo	medio	alto	Sum
Biol	23	26	14	63
Esta	29	29	8	66
Farm	30	36	7	73
Fisi	27	36	19	82
Geol	18	9	18	45
Mate	21	25	7	53
Quim	31	24	8	63
Sum	179	185	81	445

Tabla de contingencia $\mathbf{K}$

Término general $k_{ij}$
Marginal de filas $k_{i \cdot}$
Marginal de columnas $k_{\cdot j}$
Total $k=k_{\cdot\cdot}$

Tabla de frecuencias relativas#

F<-K/sum(K)
addmargins(round(F*100,2))

A matrix: 8 × 4 of type dbl
	bajo	medio	alto	Sum
Biol	5.17	5.84	3.15	14.16
Esta	6.52	6.52	1.80	14.84
Farm	6.74	8.09	1.57	16.40
Fisi	6.07	8.09	4.27	18.43
Geol	4.04	2.02	4.04	10.10
Mate	4.72	5.62	1.57	11.91
Quim	6.97	5.39	1.80	14.16
Sum	40.23	41.57	18.20	100.00

Tabla de frecuencias relativas $\mathbf{F} = \frac{1}{k}\mathbf{K}$

Termino general $f_{ij}=\frac{k_{ij}}{k}$
Marginal de filas $f_{i \cdot}$
Marginal de columnas $f_{\cdot j}$
Total $f_{\cdot\cdot}=1$

Perfiles fila#

Sea $\mathbf{D}_n = diag(f_{i \cdot})$, los perfiles fila son $\mathbf{D}_n^{-1} \mathbf{F}$:

# valores marginales por filas
Dn <- diag(rowSums(F))
print("Diagonal de con los valores maginales por filas:")
round(Dn*100,1)

# perfil fila
perFila <- solve(Dn)%*%F
rownames(perFila)<-rownames(F)
colnames(perFila)<-colnames(F)
print("Perfiles fila:")
round(perFila*100,1)

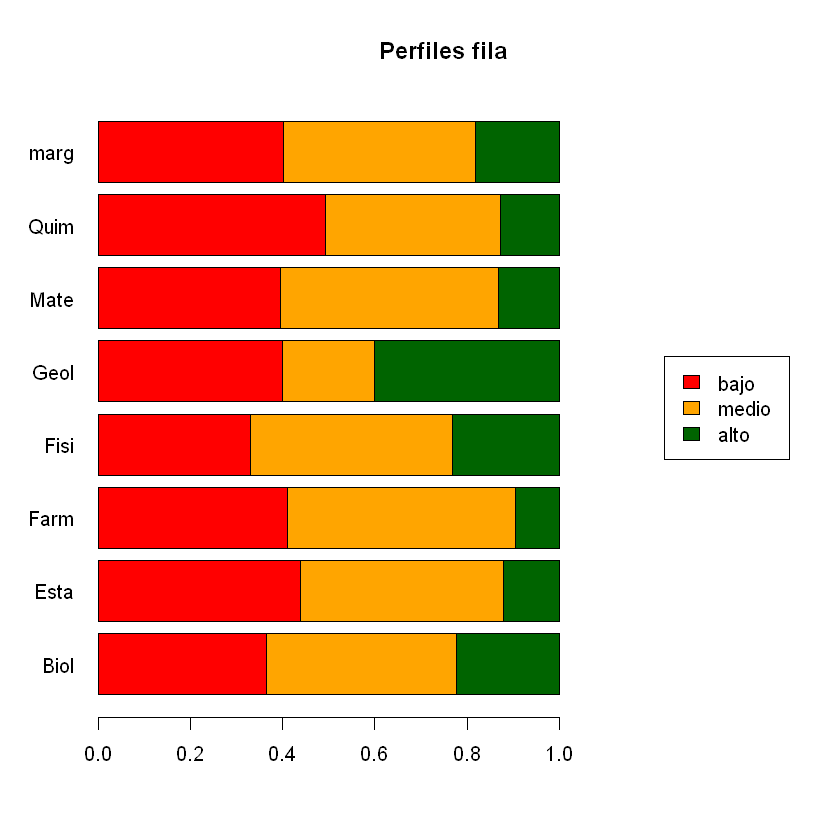
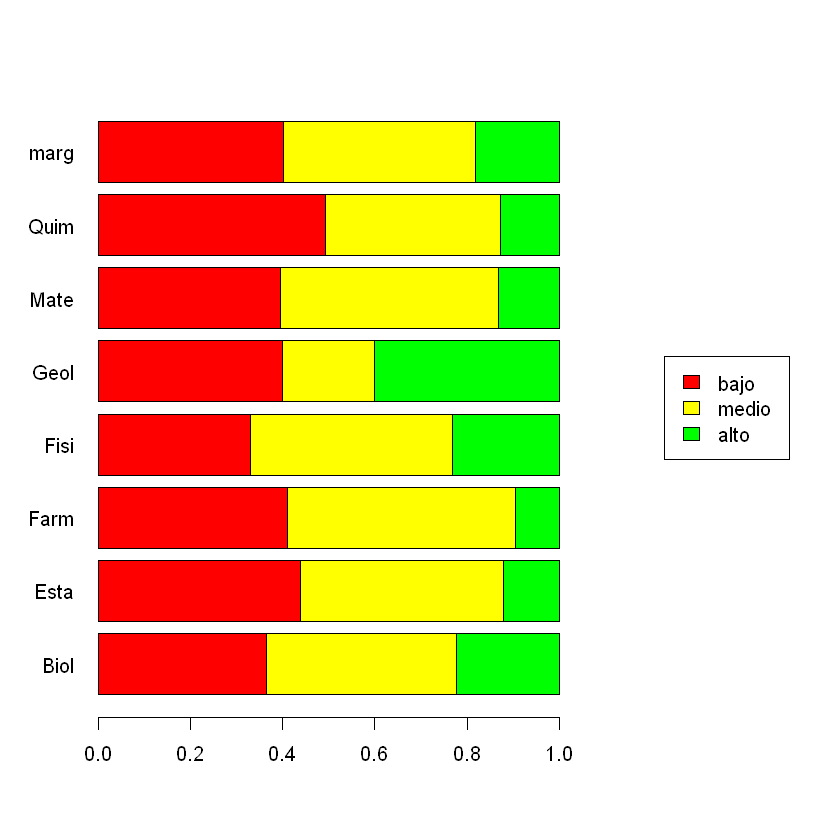
# gráfica de los perfiles
plotct(K,"row",col=c("red","orange","darkgreen"),main="Perfiles fila") #función de FactoClass

[1] "Diagonal de con los valores maginales por filas:"

A matrix: 7 × 7 of type dbl
14.2	0.0	0.0	0.0	0.0	0.0	0.0
0.0	14.8	0.0	0.0	0.0	0.0	0.0
0.0	0.0	16.4	0.0	0.0	0.0	0.0
0.0	0.0	0.0	18.4	0.0	0.0	0.0
0.0	0.0	0.0	0.0	10.1	0.0	0.0
0.0	0.0	0.0	0.0	0.0	11.9	0.0
0.0	0.0	0.0	0.0	0.0	0.0	14.2

[1] "Perfiles fila:"

A matrix: 7 × 3 of type dbl
	bajo	medio	alto
Biol	36.5	41.3	22.2
Esta	43.9	43.9	12.1
Farm	41.1	49.3	9.6
Fisi	32.9	43.9	23.2
Geol	40.0	20.0	40.0
Mate	39.6	47.2	13.2
Quim	49.2	38.1	12.7

Perfiles columna#

Sea $\mathbf{D}_p = diag(f_{\cdot j})$, los perfiles columna son $\mathbf{D}_p^{-1} \mathbf{F'}$ (puestos como filas):

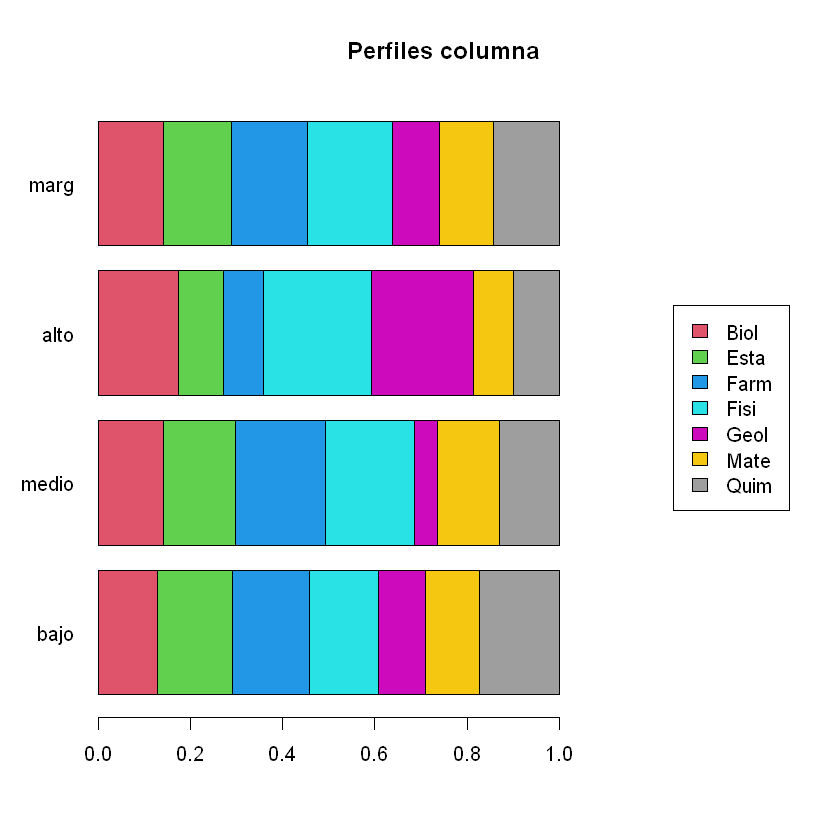
plotct(t(K),"row",col=2:8,tables=TRUE,main="Perfiles columna")->tab #función de FactoClass
Dp<-diag(colSums(F))
print("Valores maginales por columna:")
tab$perC

[1] "Valores maginales por columna:"

A matrix: 3 × 8 of type dbl
	Biol	Esta	Farm	Fisi	Geol	Mate	Quim	marg
bajo	36.5	43.9	41.1	32.9	40	39.6	49.2	40.2
medio	41.3	43.9	49.3	43.9	20	47.2	38.1	41.6
alto	22.2	12.1	9.6	23.2	40	13.2	12.7	18.2

El modelo de independencia#

Sea $a_{ij}=f_{i\cdot}f_{\cdot j}$, el término general de la tabla de independencia $\mathbf{A}$

A<-diag(Dn)%*%t(diag(Dp))
colnames(A)<-colnames(F)
round(cbind(F,A,F-A)*100,2)

A matrix: 7 × 9 of type dbl
	bajo	medio	alto	bajo	medio	alto	bajo	medio	alto
Biol	5.17	5.84	3.15	5.69	5.89	2.58	-0.53	-0.04	0.57
Esta	6.52	6.52	1.80	5.97	6.17	2.70	0.55	0.35	-0.90
Farm	6.74	8.09	1.57	6.60	6.82	2.99	0.14	1.27	-1.41
Fisi	6.07	8.09	4.27	7.41	7.66	3.35	-1.34	0.43	0.92
Geol	4.04	2.02	4.04	4.07	4.20	1.84	-0.02	-2.18	2.20
Mate	4.72	5.62	1.57	4.79	4.95	2.17	-0.07	0.67	-0.59
Quim	6.97	5.39	1.80	5.69	5.89	2.58	1.27	-0.49	-0.78

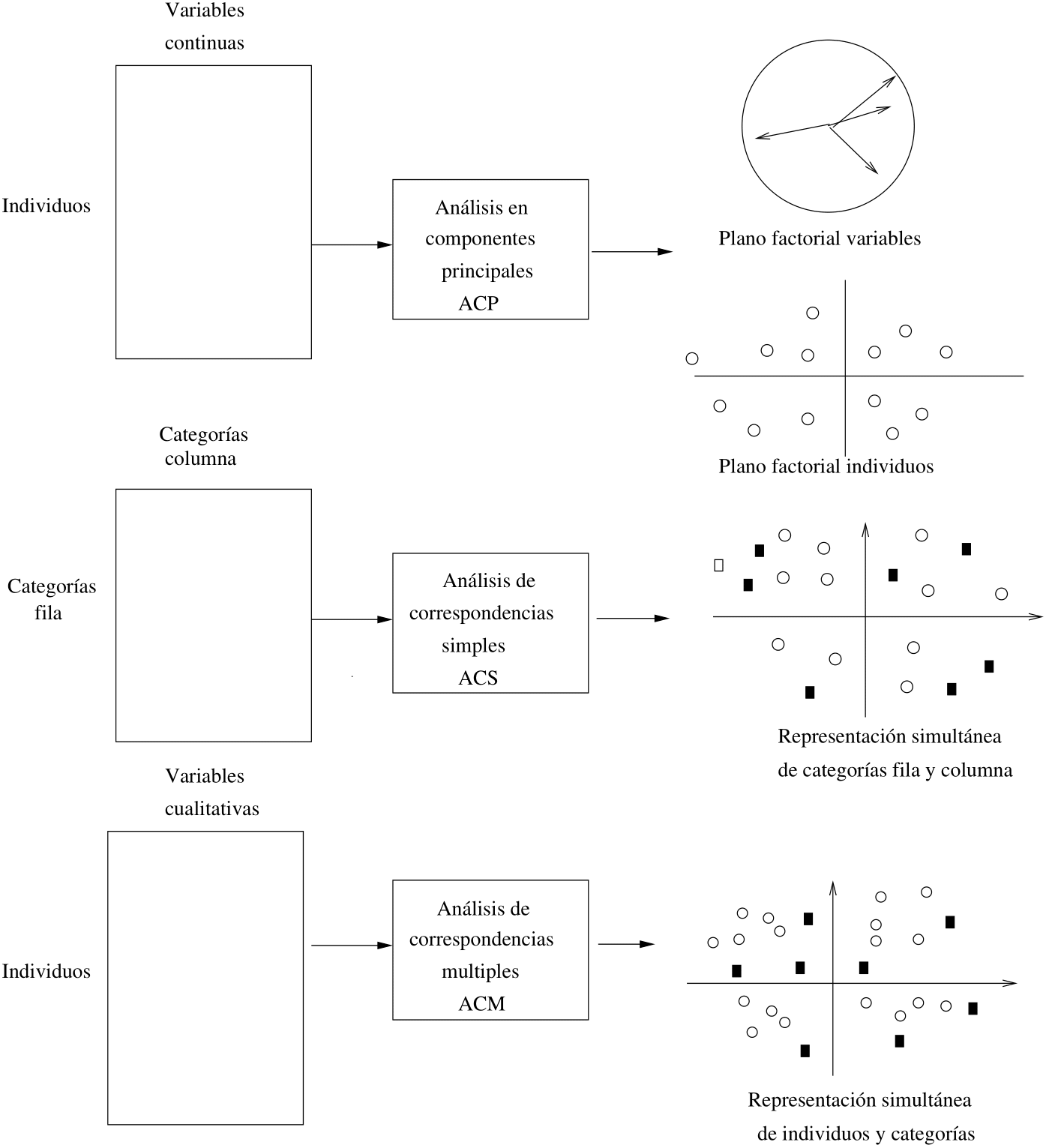
El ACS como dos ACP#

En el ACS (Análisis de Correspondencias Simple) se describen simultáneamente los perfiles fila y columna. Para cada tabla de perfiles se realiza un ACP(X, M, N), pero los dos ACP (Análisis de componentes principales) están relacionados, lo que permite representaciones simultáneas de los planos factoriales.

ACP de los perfiles-fila#

\[ ACP(\mathbf{X,M,N}) = ACP(\mathbf{D}_n^{-1}\mathbf{F},\mathbf{D}^{-1}_p,\mathbf{D_n}) \]

Se analiza la tabla de perfiles fila, entonces el histograma que respresenta un perfil fila se ve como un punto en $\mathbb{R}^p$.
La diferencia entre dos histogramas = distancia entre los puntos en $\mathbb{R}^p$.
Los pesos de los puntos fila: $f_{i\cdot}$ están en la la matriz diagonal $\mathbf{D_n}$.
Las distancias entre distribuciones condicionales se definen a partir del producto punto dado por la matriz $\mathbf{D}^{-1}_p$.
La matriz $\mathbf{D}_n^{-1}\mathbf{F}$ no está centrada.
El mayor valor propio de la matriz a diagonalizar $\mathbf{F'D_n^{-1}FD_p^{-1}}$ es 1 y el vector propio asociado es el centro de gravedad de la nube.
Partir del segundo vector propio de esta matriz es equivalente a centrar, logrando una simplificación de las fórmulas del ACS.

Nube de perfiles fila#

Coordenadas de los perfiles fila son: $\mathbf{x}_i; i=1,2,\cdots,n$; con: $$ \mathbf{x}_i(j) = \dfrac{f_{ij}}{f_{i\cdot}}; \ j=1,2,\cdots,p$$
- Si tomamos $i=3$, se obtiene el perfil de Farmacia cuyas coordenadas son $\mathbf{x}_3 =[ 0.411,0.493, 0.096]'$

Centro de gravedad: $$ \mathbf{g}_p = \sum_{i=1}^n f_{i\cdot} \mathbf{x}_i$$
- La coordenada $j$, notada $ \mathbf{g}_p(j)$, del centro de gravedad es: $$ \mathbf{g}_p(j)=\sum_{i=1}^n f_{i\cdot} \dfrac{f_{ij}}{f_{i\cdot}} = \sum_{i=1}^n f_{ij} = f_{\cdot j} $$
- Centro de gravedad = Marginal columna de la tabla F, en el ejemplo es $ \mathbf{g}_p =[0.402, 0.416, 0.182]'$

Distancia entre perfiles fila = distancia $ji$ cuadrado o de Benzècri: la métrica es $\mathbf{D}^{-1}_p$, elemento diagonal $\dfrac{1}{f_{\cdot j}}$ $$ d^2(i,l)=\sum_{j=1}^p \dfrac{1}{f_{\cdot j}} (x_{ij}-x_{lj})^2 = \sum_{j=1}^p \dfrac{1}{f_{\cdot j}} \left(\dfrac{f_{ij}}{f_{i\cdot}}-\dfrac{f_{lj}}{f_{l\cdot}}\right)^2 $$
Amplifica más las diferencias al cuadrado entre coordenadas cuando se deben a columnas de baja frecuencia marginal.
La distancia $ji$ cuadrado le confiere al ACS dos propiedades: + La equivalencia distribucional + Las relaciones cuasi-baricéntricas,

Inercia de la nube de perfiles fila: $$ Inercia(N_n) = \sum_{i=1}^n f_{i\cdot } d^2(i,\mathbf{g}_p)= \sum_{i=1}^n f_{i\cdot } \sum_{j=1}^p \dfrac{1}{f_{\cdot j}} \left(\dfrac{f_{ij}}{f_{i\cdot}}-f_{\cdot j}\right)^2= \sum_{i=1}^n \sum_{j=1}^p \frac{\left(f_{ij} - f_{i\cdot}f_{\cdot j}\right)^2}{f_{i\cdot}f_{\cdot j}} $$

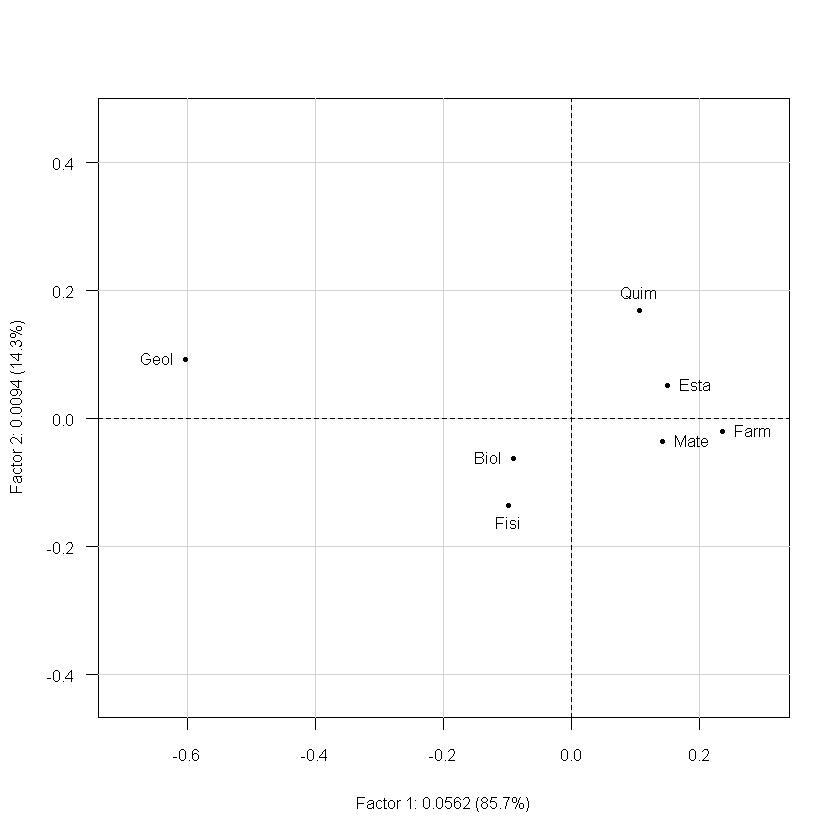
Ejes y subespacios vectoriales#

acs<-dudi.coa(K,scannf=FALSE) 
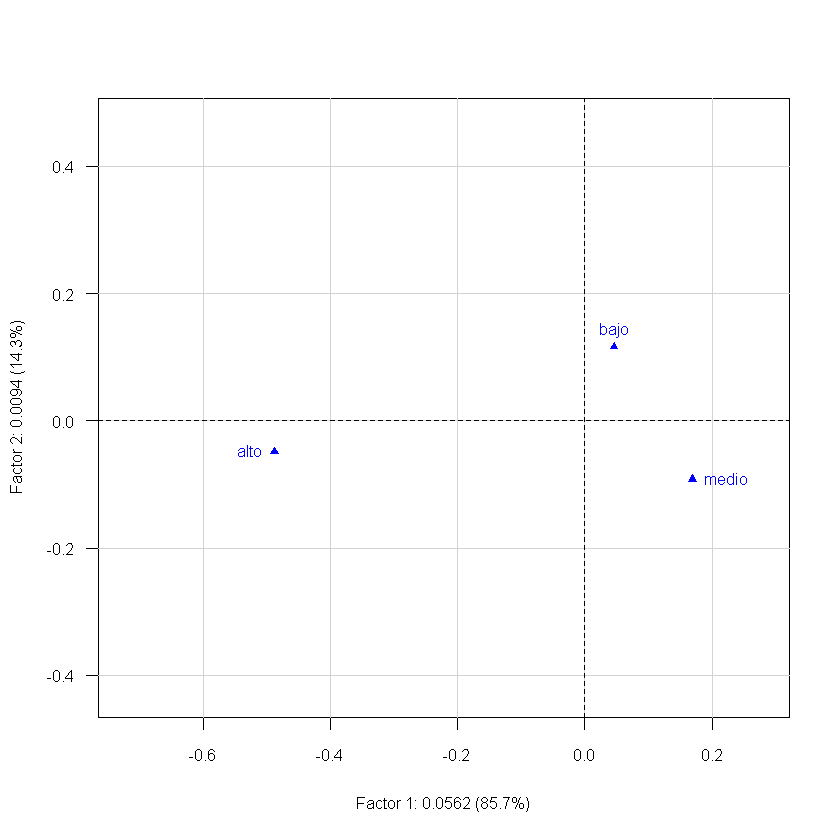
plot(acs,Tcol=FALSE,xlim=c(-0.7,0.3),cframe=1,asp=1) 
plotct(K,"row",col=c("red","yellow","green"))

ACP de los perfiles-columna#

\[ACP(\mathbf{D}_p^{-1}\mathbf{F'},\mathbf{D}_n^{-1},\mathbf{D}_p)\]

Los histogramas de las distribuciones condicionales columna se representan como puntos en $\mathbb{R}^n$
A cada punto $j$ se le asigna el peso $f_{\cdot j}$
Este análisis es simétrico al de perfiles fila

Primer plano factorial de los perfiles de estratos según carreras#

plot(acs,Trow=FALSE,asp=1) 
plotct(t(K),"row",col=2:8)

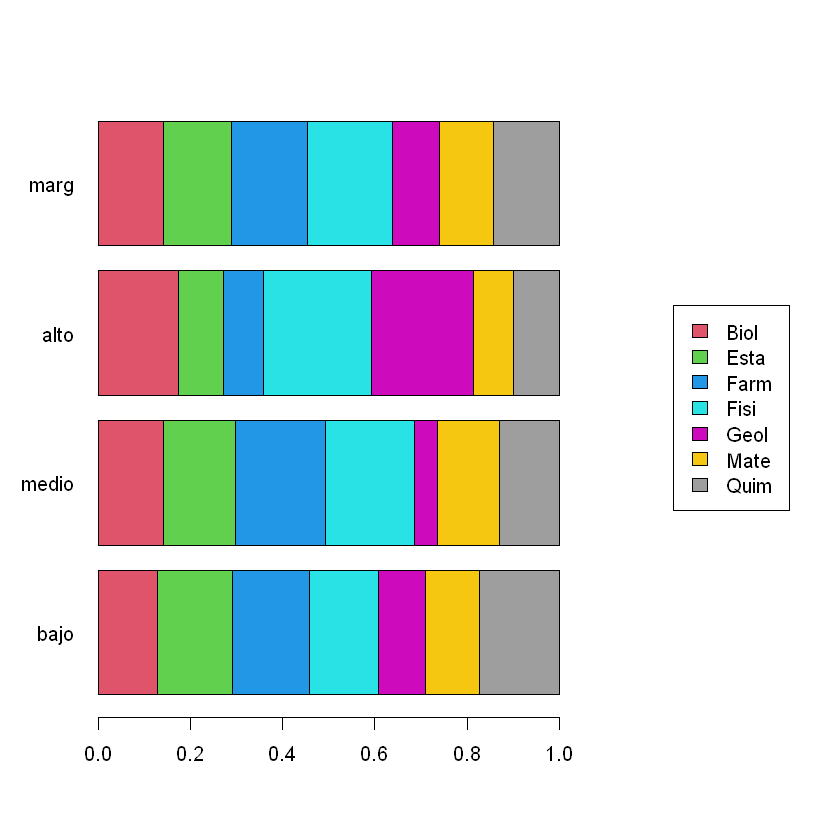
El ACS como un ACP(X,M,N)#

El ACS de la tabla $\mathbf{F}$ también se obtiene mediante el ACP de la tabla $\mathbf{X}$
Usando $\mathbf{N}=\mathbf{D}_n=diag(f_{i\cdot})$, como pesos de las filas y matriz de métrica en el espacio de las columnas.
Usando $\mathbf{M}=\mathbf{D}_p=diag(f_{\cdot j})$, como pesos de las columnas y matriz de métrica en el espacio de las filas.
Y usando $ x_{ij} =\frac{f_{ij} -f_{i\cdot} f_{\cdot j} }{f_{i\cdot} f_{\cdot j} } $

Equivalencia distribucional#

El ACS no se modifica si se unen dos puntos que tienen el mismo perfil.
El peso del punto colapsado es la suma de los pesos de los puntos que se unen.
Lo anterior permite unir filas o columnas con perfiles parecidos, para simplificar las tablas originales
- Por ejemplo las carreras Estadística, Matemáticas y Farmacia; o las carreras Biología y Física
Esta propiedad hace que el ACS sea robusto ante la «arbitrariedad» en la conformación de las categorías de una variable en un estudio

Relaciones cuasibaricéntricas#

\[ F_s(i) = \frac{1}{\sqrt{\lambda_s}}\sum_{j=1}^p{\frac{f_{ij}}{f_{i\cdot}} G_s(j)} \]

\[ G_s(j) = \frac{1}{\sqrt{\lambda_s}}\sum_{i=1}^n{{\frac{f_{ij}}{f_{\cdot j}} F_s(i)}} \]

Las relaciones cuasibaricéntricas hacen posible la representación simultánea y su interpretación.
Un sumando $j$ es $\dfrac{f_{ij}}{f_{i\cdot}} G_s(j)$, donde $\dfrac{f_{ij}}{f_{i\cdot}}$ es la coordenada $j$ del perfil de la fila $i$, es decir la altura de la barra $j$ del histograma.
Como $\sum\limits_{j=1}^p \frac{f_{ij}}{f_{i\cdot}}=1$, la sumatoria es un promedio ponderado de las coordenadas de las columnas.
Cada fila tiene un promedio diferente porque las ponderaciones cambian.
El punto promedio se ubica dentro del polígono que une a los puntos columna, por las dilataciones $\dfrac{1}{\sqrt{\lambda_s}}; s=1,2$, el punto puede ubicarse afuera.

Fuente: Alfonso Zavaleta

Ejemplo#

Coordenada del perfil de Geología sobre el primer eje (-0.604). Teniendo en cuenta que:

Perfil de Geología [0.4 0.2 0.4]
Coordenadas de los estratos sobre el primer eje [0.0458 0.1695 -0.4884]
Primer valor propio = 0.0562
La relación de transición que expresa la coordenada del perfil geología en función de las coordenadas de los perfiles columnas es: $$ \dfrac{1}{\sqrt{0.0562}} * (0.4*0.0458 + 0.2*0.1695 - 0.4*0.4884)= 4.2182 * (0.0118 + 0.0339 - 0.1954) = $$4.2182 * (-0.1497) = -0.6315 $$
El promedio ponderado por el perfil de Geología es -0.1497, se aleja del centro debido a la la dilatación por 4.2182
La coordenada de estrato alto es la que más suma, por: la ponderación (0.4) y es la que está más alejada del origen (-0.4884)

# Haciendo el cálculo
round(1/sqrt(acs$eig[1])*sum(c(0.4,0.2,0.4)*acs$co[,1]),3)

-0.604

Representación simultánea#

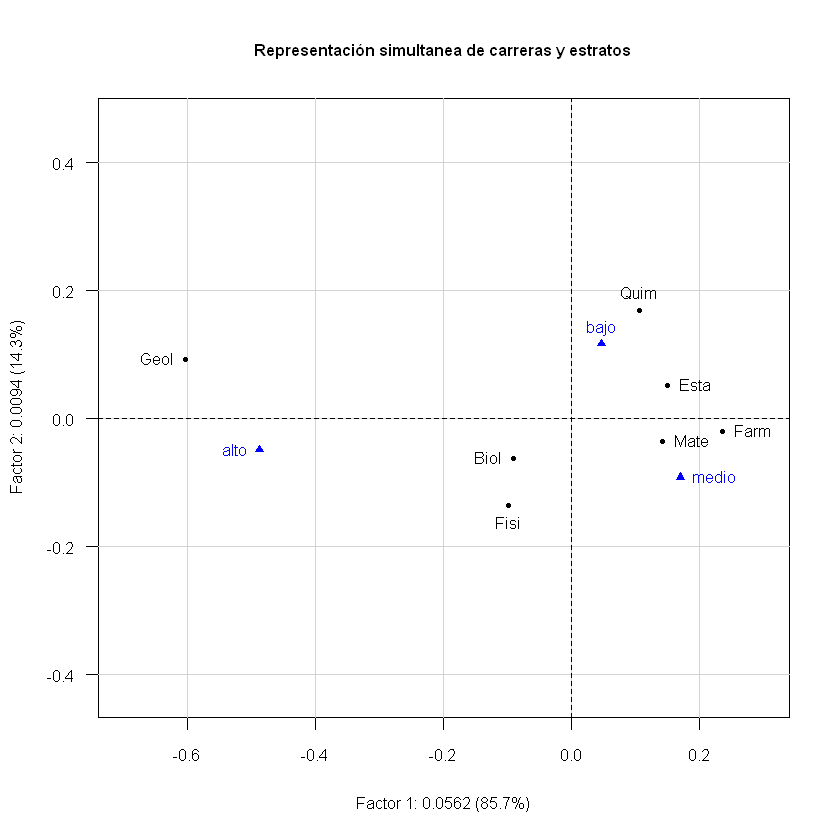
# Representación de carreras y estratos
plot(acs,xlim=c(-0.7,0.3),cframe=1,main="Representación simultanea de carreras y estratos")

ayuacs<-inertia(acs,T,T)
names(ayuacs)
# carreras
round(cbind(acs$li,Ca=ayuacs$row.abs,cos2=ayuacs$row.rel,conInercia=ayuacs$row.contrib),2)
# estratos
round(cbind(acs$co,Ca=ayuacs$col.abs,cos2=ayuacs$col.rel,conInercia=ayuacs$col.contrib),2)

'tot.inertia'
'row.contrib'
'row.abs'
'row.rel'
'row.cum'
'col.contrib'
'col.abs'
'col.rel'
'col.cum'
'nf'
'call'

A data.frame: 7 × 7
	Axis1	Axis2	Ca.Axis1	Ca.Axis2	cos2.Axis1	cos2.Axis2	conInercia
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
Biol	-0.09	-0.06	2.14	5.79	-68.86	-31.14	2.66
Esta	0.15	0.05	5.89	4.39	88.91	11.09	5.67
Farm	0.23	-0.02	16.05	0.67	99.30	-0.70	13.85
Fisi	-0.10	-0.13	3.26	35.61	-35.43	-64.57	7.90
Geol	-0.60	0.09	65.58	9.16	-97.72	2.28	57.50
Mate	0.14	-0.04	4.26	1.57	94.20	-5.80	3.87
Quim	0.11	0.17	2.82	42.81	28.29	71.71	8.55

A data.frame: 3 × 7
	Comp1	Comp2	Ca.Axis1	Ca.Axis2	cos2.Axis1	cos2.Axis2	conInercia
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
bajo	0.05	0.12	1.50	58.27	13.35	86.65	9.63
medio	0.17	-0.09	21.26	37.17	77.39	-22.61	23.54
alto	-0.49	-0.05	77.24	4.56	-99.02	-0.98	66.83

Imprimiendo el objeto acs podemos obtener una lista de todas las características extraibles de este objeto:

acs

Duality diagramm
class: coa dudi
$call: dudi.coa(df = K, scannf = FALSE)

$nf: 2 axis-components saved
$rank: 2
eigen values: 0.0562 0.009393
  vector length mode    content       
1 $cw    3      numeric column weights
2 $lw    7      numeric row weights   
3 $eig   2      numeric eigen values  

  data.frame nrow ncol content             
1 $tab       7    3    modified array      
2 $li        7    2    row coordinates     
3 $l1        7    2    row normed scores   
4 $co        3    2    column coordinates  
5 $c1        3    2    column normed scores
other elements: N 

Ayudas para la interpretación#

Contribución absoluta La contribución de un perfil a la varianza del eje (inercia proyectada), depende del peso y de la coordenada al cuadrado: $$Ca_s(i) = \dfrac{f_{i\cdot}(F_s(i))^2}{\lambda_s}$$
Coseno cuadrado Calidad de la representación o contribución relativa: $$Cos^2_s(i) = \dfrac{(F_s(i))^2}{d^2(i,\mathbf{g})}$$
¿Por qué cree que se da el nombre de contribución relativa? $$Cos^2_s(i) = \dfrac{F_s^2(i)}{d^2(i,\mathbf{g})} = \dfrac{f_{i\cdot} F_s^2(i)} {f_{i\cdot} d^2(i,\mathbf{g})}$$
Contribuciones del punto a la inercia: proyectada sobre el eje $s$ / en el espacio completo - Inercia sobre el eje $s$: $\sum\limits_{i=1}^n f_{i\cdot} F^2_s(i)$ - Inercia en $\mathbb{R}^p$: $\sum\limits_{i=1}^n f_{i\cdot} d^2(i,\mathbf{g})$

Filas y columnas suplementarias#

Se proyectan e interpretan utilizando las fórmulas de transición.
Su interpretación debe hacerse después de la de los elementos activos.
AYUDAS
- Distancia al origen
- Coseno cuadrado
- Valor test

Ejemplo de aplicación#

Ver el ejemplo del capítulo 5 del libro Estadística descriptiva multivariada - Facultad de Ciencias, Campo Elías Pardo y los talleres.

Ejercicio#

Realizar un análisis de correspondencias simples de una tabla de su interés.

Fundamentos de IA y AP

Análisis de correspondencias simples

Contents

Análisis de correspondencias simples#

Objetivos de ACS#

Ejemplo «de juguete» y notación#

Tabla de contingencia#

Tabla de frecuencias relativas#

Perfiles fila#

Perfiles columna#

El modelo de independencia#

El ACS como dos ACP#

ACP de los perfiles-fila#

Nube de perfiles fila#

Ejes y subespacios vectoriales#

ACP de los perfiles-columna#

Primer plano factorial de los perfiles de estratos según carreras#

El ACS como un ACP(X,M,N)#

Equivalencia distribucional#

Relaciones cuasibaricéntricas#

Ejemplo#

Representación simultánea#

Ayudas para la interpretación#

Filas y columnas suplementarias#

Ejemplo de aplicación#

Ejercicio#