Introducción a Redes Neuronales
Contents
Introducción a Redes Neuronales#
Introducción

Fuente: imágenes libres en pixabay
¿Qué es una Red Neuronal Artificial?#
Las Redes Neuronales Artificiales son modelos computacionales inspirados en el cerebro humano. Muchos de los avances recientes en ciencia y tecnología se han hecho en el campo de la Inteligencia Artificial, que van desde reconocimiento de voz hablada, reconocimiento de imágenes, y robótica, entre otros.
Como se dijo anteriormente, las Redes Neuronales Artificiales son simulaciones inspiradas en el ámbito biológico hechas en un ordenador para realizar tareas como
Clustering
Clasificación
Reconocimiento de Patrones
Aunque en general, se usan para resolver objetivos específicos guiados por su creador.
Somos Electricidad#

Fuente: pixabay: imágenes libres
Partes de una Neurona y sus Funciones#
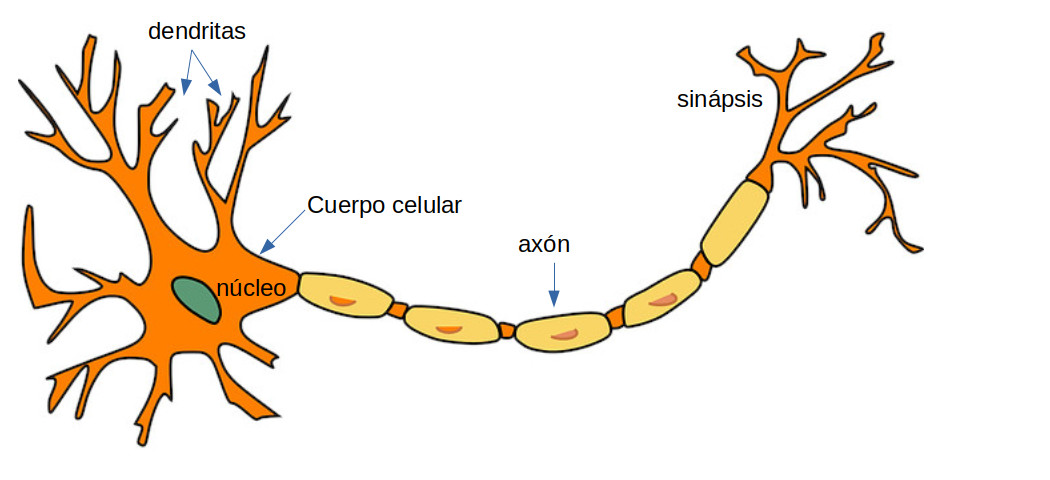
Fuente: Alvaro Montenegro, basado en una imagen de pixabay
Las células nerviosas típicas del cerebro humano se compone de cuatro partes:
Función de la Dendrita. Recibe las señales de otras neuronas.
Soma (cuerpo celular). Suma todas las señales entrantes para generar una señal total de entrada(input).
Estructura del Axón. Cuando la suma sobrepasa un cierto umbral numérico, la neurona se activa, dispara y la señal viaja a través del axón hacia otras neuronas.
Trabajo de la Sinapsis. Es el punto donde se realiza la interconexión de una neurona con otras neuronas. La cantidad de la señal transmitida depende en la fuerza (peso sináptico) de las conexiones. Las conexiones pueden ser inhibidoras (disminuyendo la fuerza) o de excitación (aumentando la fuerza) en principio.
Así pues, una Red Neuronal es, en general una red altamente interconectada de billones de neuronas con trillones de interconexiones entre ellas.
Fuente: Pixabay: imágenes libres
Comparación entre Redes Neuronales Biológicas y Artificiales#

Fuente: Pixabay: imágenes libres
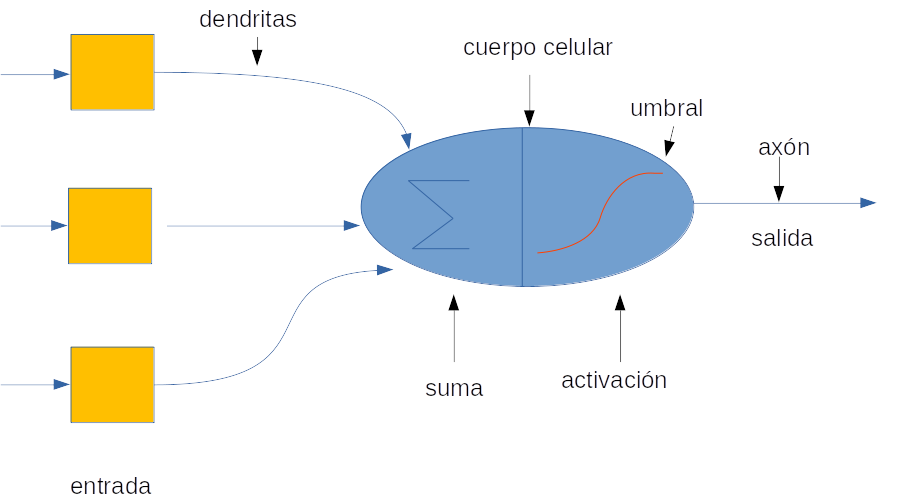
Fuente: Alvaro Montenegro
Fuente: ClipArtMax
Las dendritas in las Redes Neuronales Biológicas son un análogo a las entradas conteniendo un peso especifico basada en la interconexión «sináptica» presente en la Red Neuronal Artificial.
El cuerpo celular es comparable a la unidad artificial llamada «neurona» en una Red Neuronal Artificial, que también comprende la suma de señales y umbral de activación.
La salida de los Axones (presentes en la sinapsis) son el análogo de los datos de salida en la Red Neuronal Artificial.
Por lo tanto, RNA son modeladas usando el trabajo básico de las neuronas biológicas.
Arquitecturas de redes neuronales modernas#
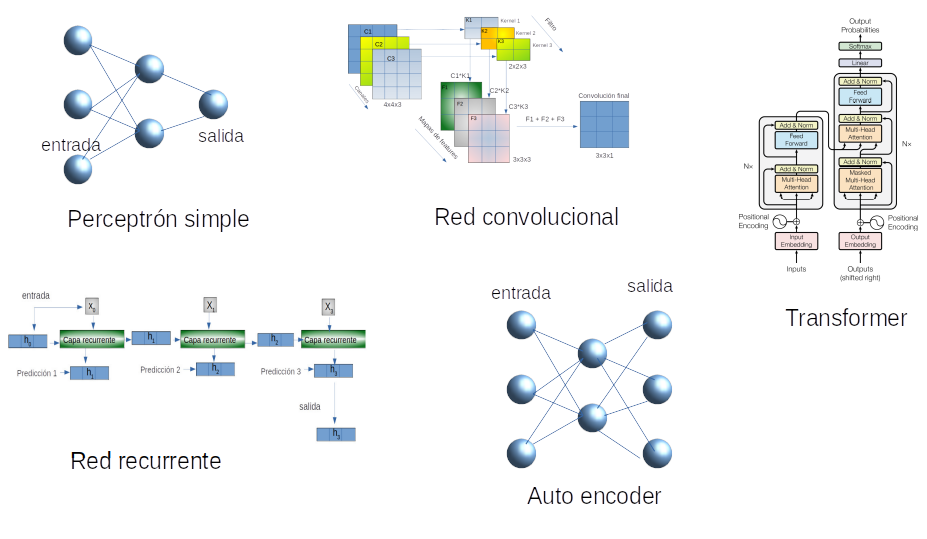
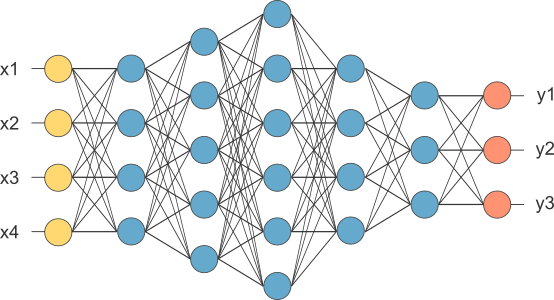
Fuente: Alvaro Montenegro
Red neuronal de perceptrón multicapa. Estas redes utilizan más de una capa oculta de neuronas, a diferencia del perceptrón de una sola capa. También se conocen como Redes neuronales de alimentación profunda.
RNA convolucional. Esta redes se basan en el concepto matemáticos de convolución. Esencialmente se basan en filtros que se aplican por ejemplo a las imágenes. Los filtros son estimados para cada red.
Transformer. Estas redes son especiales para el tratamiento de procesamiento de lenguaje natural. Recientemente han sido aplicadas a series de tiempo e imágenes. Se basan en el concepto de auto-atención.
Red neuronal recurrente. Tipo de red neuronal en la que las neuronas de cada capa oculta tienen auto-conexiones. Las redes neuronales recurrentes poseen memoria. En cualquier caso, la neurona de capa oculta recibe la activación de la siguiente capa, así como su valor de activación anterior. Muy usadas principalmente emn series de tiempo. Los modelos más conocidos con LSTM y GRU.
Red autocodificadora o auto-encoder. Es esencialmente un perceptrón multicapa de múltiples usos como parte de otras arquitecturas. Por sí mismas son útiles para hacer reducción de dimensión de los datos.
Enfoque Matemático de una RNA#
¿Cómo funciona una Red Neuronal Artificial?#
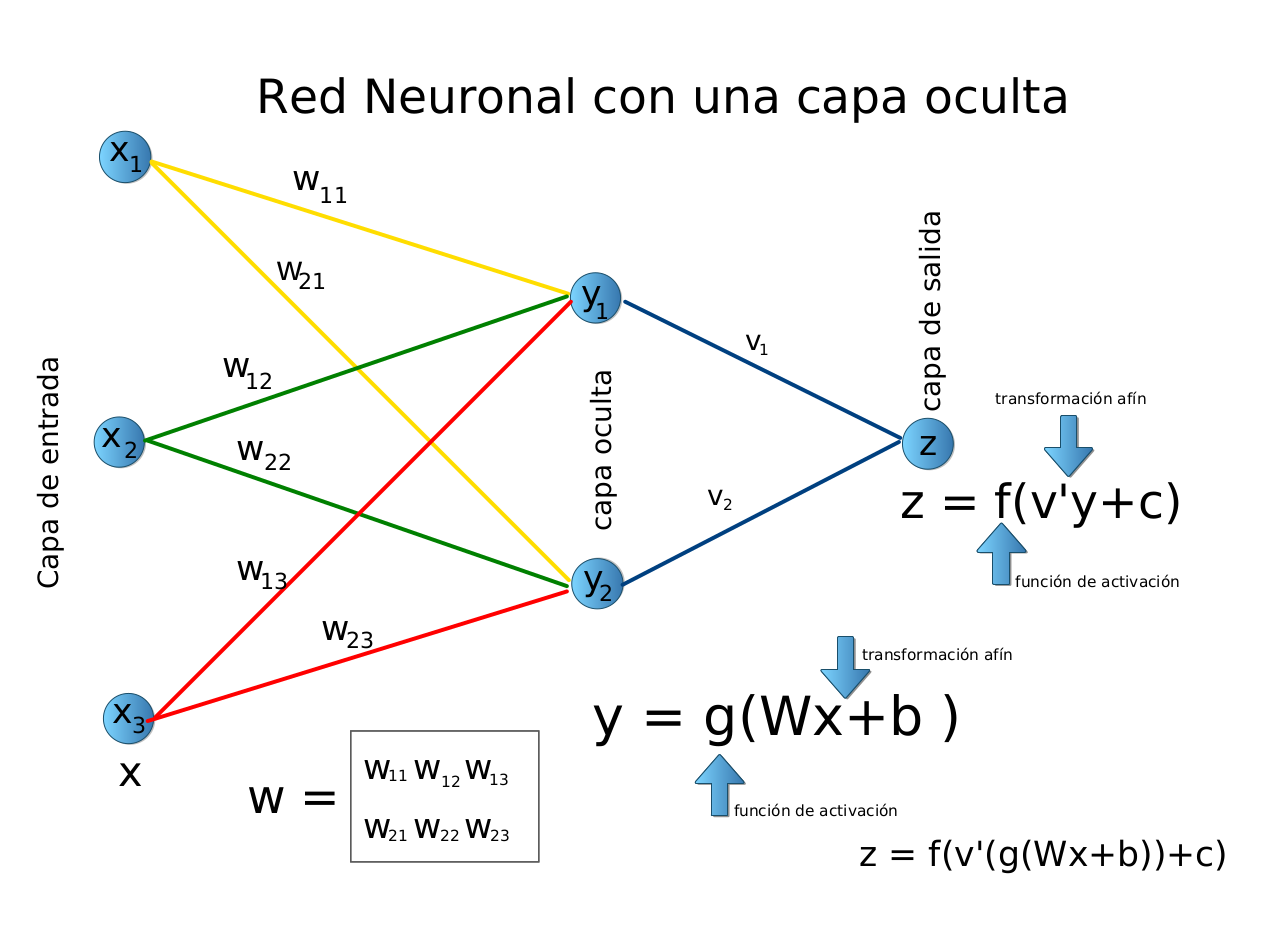
Fuente: Alvaro Montenegro
La red neuronal artificial recibe información del mundo externo en forma de patrón en forma de vector, digamos \(x=(x_1,\ldots,x_n)^t\). En este caso, la capa de entrada posee \(n\) neuronas artificiales.
Cada componente \(x_i\) de la entrada se multiplica por el peso correspondiente \(w_{i}\). Los pesos son la información utilizada por la red neuronal para resolver un problema específico. Estos pesos deben aprenderse (ajustarse, estimarse) en el paso de entrenamiento. Los pesos representan el conocimiento que tienen los ANN sobre el problema en cuestión.
Usando la metáfora biológica, los pesos representan la fuerza de la interconexión entre las neuronas dentro de la red neuronal.
Las entradas y los pesos se combinan y se resumen dentro de la unidad de computación (neurona artificial), y se agrega un «sesgo» (intercepto), como muestra la figura arriba.
La suma es un número real: \(z = \sum_i x_iw_i + b\), \(z \in\mathcal{R}\). Esta suma se transforma a través de una función de activación, digamos \(g(\cdot)\), para obtener la salida neta \(x^* = g(z)\). La función de activación determina el comportamiento de la neurona. Para más detalles, consulte la siguiente sección.
Supuestos básicos#
La primera capa oculta de un RNA podría ser una reducción de dimensión. Sin embargo, en general, es más práctico reducir los datos previamente. Entonces, a partir de este punto, suponemos que los datos de entrenamiento son datos reducidos (si es que tal reducción es necesaria).
En esta sección consideramos sólo una capa oculta. Asumiremos que:
La capa de entrada tiene \(n\) neuronas. Entonces los valores de entrada son \(n\)-vectores.
La capa oculta tiene \(q\) neuronas. Esto implica que existen conexiones \(q\) desde cada neurona de entrada a la capa oculta. En total hay conexiones \(n \times q\) entre la capa de entrada y la capa oculta. Cada conexión tiene un peso \(w^{1}_{ij}\), que representa la fuerza de la conexión entre la neurona \(i\) en la capa de entrada y la neurona \(j\) en la capa oculta.
La capa de salida tiene neuronas \(L\). Esto implica que existen conexiones \(L\) de cada neurona oculta a la capa de salida. En total hay conexiones \(q \times L\) entre la capa oculta y la capa de salida. Cada conexión tiene un peso \(w^{2}_{jk}\), que representa la fuerza de la conexión entre la neurona \(j\) en la capa oculta y la neurona \(k\) en la capa de salida.
\(\leadsto\) Notación Vectorial. Por facilidad, denotaremos los vectores en un formato de fila, como es habitual en matemáticas. En estadística es común la notación de columna.
Modelo matemático de una RNA con una capa oculta#
Datos de entrenamiento#
Sea \(X_{N\times n}\) la matriz de los datos de entrenamiento de entrada \(N\).
Transformación afín de los datos.#
Sea \(W^{1}\) una matriz \(n\times q\) cuyas filas son los vectores de peso \(w^{1}_{ij}\), que conceptualmente conectan la capa de entrada con la capa oculta. Sea \(b^{1}\) el \(q\)-vector de los respectivos bias. Supongamos que \(b=(b^1_1,\ldots, b^1_j,\ldots,b^1_q)\). Entonces , \(b^1_j\) es el bias en la neurona \(j\) de la capa oculta.
Dado un vector de entrada \(x\), que es fila de matriz \(X\), la entrada completa de la capa oculta se obtiene mediante
\(\leadsto\) Note que hemos asumido que hay \(n\) neuronas en la capa de entrada. Si \(q<n\), \(W^{1}\) realiza una proyección sobre un subespacio de dimensión reducida. Si \(q>n\), \(W^{1}\) realiza un «sumergimiento» (embedding) sobre un espacio de dimensión mayor.
La ecuación (1) es una transformación afín, que puede ser expresada en coordenadas homogéneas de la siguiente manera:
\(\tilde{x} = (x,1)\), \(\tilde{z}^1 = (z^1,1)\). Let \(\tilde{W}\) defined as:
por lo que obtenemos,
Esta ecuación significa que una transformación afín se puede expresar como una transformación lineal en coordenadas homogéneas. Para obtener más información, consulte la próxima lección, sobre transformaciones afines.
Activación de Neuronas en la capa oculta#
Sea \(f^1\) la función de activación en la capa oculta. Entonces, \(f^1\) se aplica a cada elemento de \(z^1\). Sea \(x^1 = (x_1^1,\ldots,x_j^1,\ldots, x_q^1)\). El efecto de la función de activación se escribe como
donde \(x^1_j = f^1(z^1_j)\), para \(j=1,\ldots,q\).
Desde la capa oculta a la capa de salida#
Transformación afín de los datos#
Supongamos que \(W^{2}\) es una matriz \(q\times L\), cuyas filas son los vectores de pesos \(w^{2}_{jk}\), que conceptualmente conecta la capa oculta con la capa de salida. Sea \(b^{2}\) el \(L\)-vector de los correspondientes biases (interceptos).
\(\leadsto\) En la aplicación de una Red Neuronal Profunda a un problema de clasificación, \(L\) corresponde al número de clases.
Dado \(x^1\) el vector de salida de la capa oculta, la entrada completa a la capa de salida se obtiene como
En coordenadas homogéneas, tenemos que
Activación de Neuronas en la capa de salida#
Sea \(f^2\) la función de activación en la capa de salida. Entonces, \(f^2\) se aplica a cada elemento de \(z^2\). Sea \(y = (y_1,\ldots,y_k,\ldots, y_L)\). El efecto de la función de activación se escribe como
donde \(y_k = f^2(z^2_k)\), for \(k=1,\ldots,L\).
¿Por qué necesitamos funciones de activación no lineales?#
Una red neuronal sin funciones de activación lineal es esencialmente un modelo de regresión lineal. La función de activación realiza una transformación no lineal de la entrada, lo que la hace capaz de aprender y realizar tareas más complejas.
Para ver este hecho, suponga que \(\tilde{G}^1\) y \(\tilde{G}^2\) representan las matrices asociadas a las funciones de activación lineal en coordenadas homogéneas. Por lo tanto, tenemos que
donde $\( \tilde{W}=\tilde{W}^1\tilde{G}^1\tilde{W}^2\tilde{G}^2 \)$ .
\(\leadsto\) Así, en este caso la RNP se reduce a un modelo lineal simple, que no es muy útil en la práctica.
Una RNA es una función vectorial#
Una RNA con una capa oculta es una función \(f:\mathcal{R}^n \to \mathcal{R}^L\), definida como
\(\leadsto\) Como puede verse, si la RNA tiene más de una capa oculta, la función \(f\) puede ser extendida directamente de forma recursiva.


