Optimización univariada usando JAX
Contents
Optimización univariada usando JAX#
Introducción#
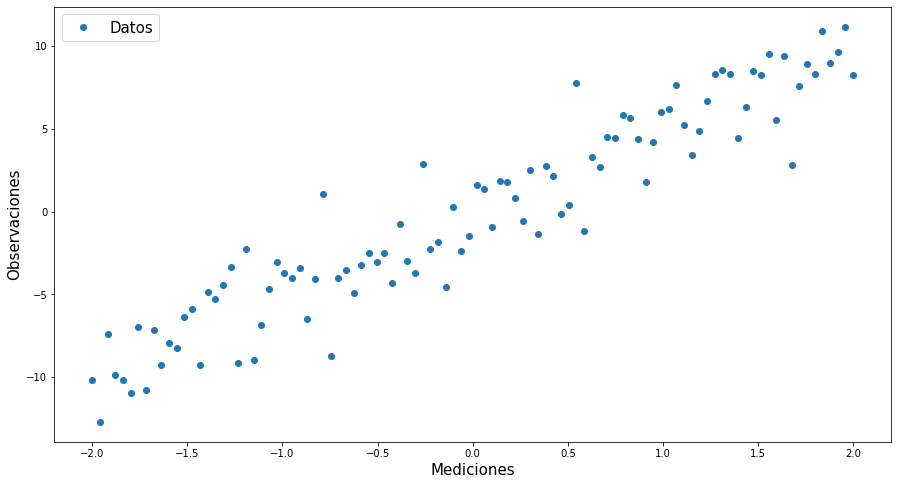
En este ejercicio generamos un conjunto de datos que sigue un modelo lineal, pasando por el origen. Los datos son contaminados con un error normal \(N(0,2^2)\).
Carga módulos#
from __future__ import print_function
import jax.numpy as np # autograd para windows
import numpy as onp
import matplotlib.pyplot as plt
from jax import grad,jit
import pandas as pd
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [1], in <cell line: 2>()
1 from __future__ import print_function
----> 2 import jax.numpy as np # autograd para windows
3 import numpy as onp
4 import matplotlib.pyplot as plt
File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\__init__.py:21, in <module>
18 del _os
20 # flake8: noqa: F401
---> 21 from .config import config
22 from .api import (
23 ad, # TODO(phawkins): update users to avoid this.
24 argnums_partial, # TODO(phawkins): update Haiku to not use this.
(...)
87 xla_computation,
88 )
89 from .experimental.maps import soft_pmap
File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\config.py:19, in <module>
17 import threading
18 from typing import Optional
---> 19 from jax import lib
21 def bool_env(varname: str, default: bool) -> bool:
22 """Read an environment variable and interpret it as a boolean.
23
24 True values are (case insensitive): 'y', 'yes', 't', 'true', 'on', and '1';
(...)
30 Raises: ValueError if the environment variable is anything else.
31 """
File ~\AppData\Local\Programs\Python\Python39\lib\site-packages\jax\lib\__init__.py:23, in <module>
1 # Copyright 2018 Google LLC
2 #
3 # Licensed under the Apache License, Version 2.0 (the "License");
(...)
15 # This module is largely a wrapper around `jaxlib` that performs version
16 # checking on import.
18 __all__ = [
19 'cuda_prng', 'cusolver', 'rocsolver', 'jaxlib', 'lapack',
20 'pocketfft', 'pytree', 'tpu_client', 'version', 'xla_client'
21 ]
---> 23 import jaxlib
25 # Must be kept in sync with the jaxlib version in build/test-requirements.txt
26 _minimum_jaxlib_version = (0, 1, 60)
ModuleNotFoundError: No module named 'jaxlib'
Genera y grafica datos simulados#
# Simulación de los Datos
# Se escoge una semilla
onp.random.seed(22)
# Generación de los datos
x=onp.linspace(-2,2,100)
y=5*x+2*onp.random.normal(0,1,len(x))
#Print Results
#print("x:\n",x,"\n")
#print("y:\n",y)
data=pd.DataFrame({"Mediciones":x,"Observaciones":y})
data
| Mediciones | Observaciones | |
|---|---|---|
| 0 | -2.000000 | -10.183900 |
| 1 | -1.959596 | -12.724681 |
| 2 | -1.919192 | -7.432376 |
| 3 | -1.878788 | -9.872590 |
| 4 | -1.838384 | -10.174177 |
| ... | ... | ... |
| 95 | 1.838384 | 10.930610 |
| 96 | 1.878788 | 8.960411 |
| 97 | 1.919192 | 9.630197 |
| 98 | 1.959596 | 11.177407 |
| 99 | 2.000000 | 8.233714 |
100 rows × 2 columns
plt.figure(figsize=(15,8))
plt.plot(x,y,'o')
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos"],fontsize=15)
plt.show()
Genera y grafica datos simulados con Widgets#
from ipywidgets import interactive
import plotly
import plotly.graph_objs as go
# Simulación de los Datos
def simular_datos(σ=0,w1=0):
# Se escoge una semilla
onp.random.seed(22)
# Generación de los datos
x=onp.linspace(-2,2,100)
y=w1*x+onp.random.normal(loc=0,scale=σ,size=len(x))
data=pd.DataFrame({"Mediciones":x,"Observaciones":y})
plt.figure(figsize=(10,7))
plt.plot(x,y,'o',markersize=5)
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos"],fontsize=15)
plt.ylim([-30,30])
plt.title(f'Simulación de ${w1}x+\epsilon$, $\epsilon$ ~ N(0,σ²)')
plt.show()
return x,y
interactive_plot = interactive(simular_datos, σ=(0, 10.,0.2),w1 = (-10.,10.))
#output = interactive_plot.children[-1]
#output.layout.height = '350px'
interactive_plot
Ejemplo#
Juegue con los sliders para entender a profundidad lo que hace cada parámetro.
Función de pérdida#
def loss(w1,x,y):
return ((y-(w1*x))**2).mean()
## Diferenciación Automática
grad_loss=jit(grad(loss,argnums=(0)))
Gradiente descendiente #
\[\textbf{futuro = presente + paso}\times\textbf{cambio}\]
\[w_{1}^{n+1}=w_{1}^{n}-hL'\big|_{w_{1}^{n}}\]
def optimize(w1,x,y,h=1.5):
# Calcular Derivada
w1_grad=grad_loss(w1,x,y)
# Gradiente Descendiente
w1-=h*w1_grad
# Regresar Nuevos parámetros
return w1
Optimización#
## Estimación inicial
W1=10.
# Acumular resultados
w1=[]
train_loss=[]
# Número de veces que se cambian los parámetros
epochs=401
# Tasa de Aprendizaje
h=0.01
#0.8
print("Pérdidas:\n")
w1.append(W1)
train_loss.append(loss(W1,x,y))
print(f"Condición Inicial: Pérdida: {loss(W1,x,y)}, Parámetro: {W1}\n")
for epoch in range(epochs):
W1=optimize(W1,x,y,h)
w1.append(W1)
losss=loss(W1,x,y)
train_loss.append(losss)
if epoch%100==0:
print(f"Iteración {epoch}: Pérdida: {losss}, Parámetro: {W1}")
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
Pérdidas:
Condición Inicial: Pérdida: 38.407744806265676, Parámetro: 10.0
Iteración 0: Pérdida: 36.55500411987305, Parámetro: 9.86294937133789
Iteración 100: Pérdida: 4.018570423126221, Parámetro: 5.273087501525879
Iteración 200: Pérdida: 3.88777232170105, Parámetro: 4.982072830200195
Iteración 300: Pérdida: 3.887246608734131, Parámetro: 4.963622093200684
Iteración 400: Pérdida: 3.887244701385498, Parámetro: 4.962451457977295
print(w1[-1])
4.9624515
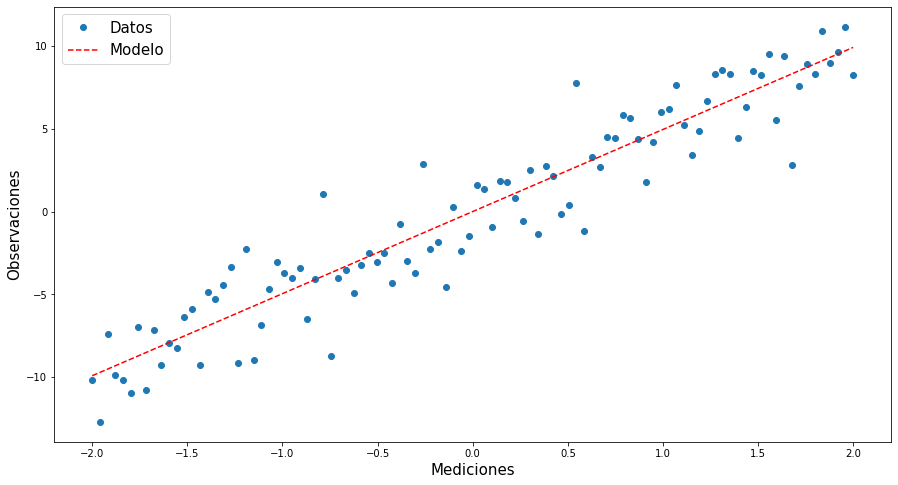
# Haciendo el Mmodelo
mod=w1[-1]*x
# Visualizando el modelo
plt.figure(figsize=(15,8))
plt.plot(x,y,'o')
plt.plot(x,mod,'r--')
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos","Modelo"],fontsize=15)
plt.show()
Usando Widgets#
def regresion(μ=0,σ=0,m=0,epochs=0,W1=0,aprendizaje=0.1):
# Se escoge una semilla
onp.random.seed(22)
# Generación de los datos
x=onp.linspace(-2,2,100)
y=m*x+2*onp.random.normal(loc=μ,scale=σ,size=len(x))
data=pd.DataFrame({"Mediciones":x,"Observaciones":y})
## Estimación inicial
W1=W1
# Acumular resultados
w1=[]
train_loss=[]
# Número de veces que se cambian los parámetros
epochs=epochs
# Tasa de Aprendizaje
h=aprendizaje
#0.8
print("Pérdidas:\n")
w1.append(W1)
train_loss.append(loss(W1,x,y))
print(f"Condición Inicial: Pérdida: {loss(W1,x,y)}, Parámetro: {W1}\n")
for epoch in range(epochs):
W1=optimize(W1,x,y,h)
w1.append(W1)
losss=loss(W1,x,y)
train_loss.append(losss)
if epoch%100==0:
print(f"Iteración {epoch}: Pérdida: {losss}, Parámetro: {W1}")
# Haciendo el modelo
mod=w1[-1]*x
plt.figure(figsize=(15,8))
plt.plot(x,y,'o')
plt.plot(x,mod,'r--')
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos","Modelo"],fontsize=15)
plt.show()
interactive_plot = interactive(regresion, σ=(0, 10.), μ=(-3, 3, 0.5),m = (-10.,10.),epochs=(0,500),W1=(-10.,10.),aprendizaje=(0.0001,1.))
#output = interactive_plot.children[-1]
#output.layout.height = '350px'
interactive_plot
Visualizando la función pérdida #
# eje β (par.)
β1x=onp.linspace(-2,11,epochs)
l=onp.empty(len(β1x))
for i in range(len(l)):
l[i]=((β1x[i]*x-y)**2).mean()
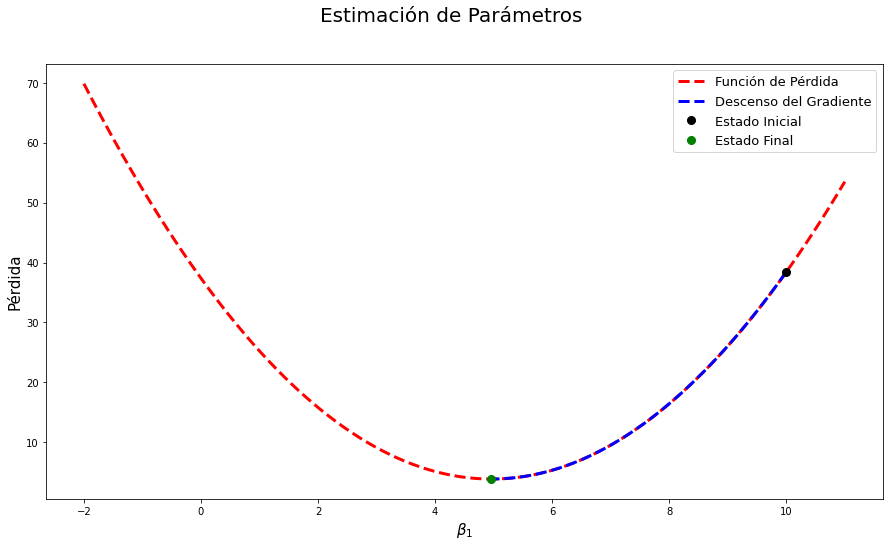
fig = plt.figure(figsize=(15,8))
plt.suptitle("Estimación de Parámetros",fontsize=20)
ax = plt.axes()
ax.plot(β1x,l,'r--',lw=3) # Función de pérdida
ax.plot(w1,train_loss,'b--',lw=3,ms=8) # Ruta tomada por el optimizador
ax.plot(w1[0],train_loss[0],'ko',ms=8) # Condición inicial
ax.plot(w1[-1],train_loss[-1],'go',ms=8) # Estado Final
ax.set_xlabel(r"$\beta_1$",fontsize=15)
ax.set_ylabel(r"Pérdida",fontsize=15)
plt.legend(["Función de Pérdida","Descenso del Gradiente","Estado Inicial","Estado Final"],fontsize=13)
plt.show()
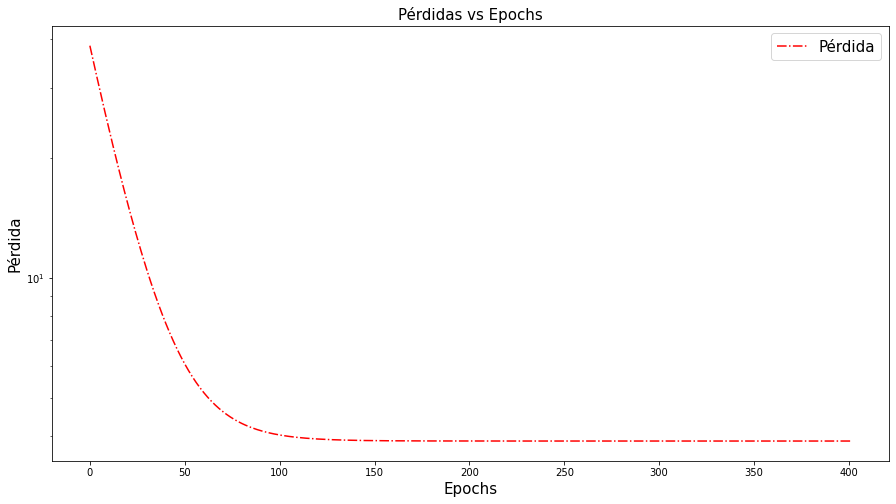
plt.figure(figsize=(15,8))
plt.semilogy(range(epochs+1),train_loss,'r-.')
plt.xlabel("Epochs",fontsize=15)
plt.ylabel("Pérdida",fontsize=15)
plt.legend(["Pérdida"],fontsize=15)
plt.title("Pérdidas vs Epochs",fontsize=15)
plt.show()
Aplicando Todo#
def regresion(μ,σ,m,epochs,W1,aprendizaje):
# Se escoge una semilla
onp.random.seed(22)
# Generación de los datos
x=onp.linspace(-2,2,100)
y=m*x+2*onp.random.normal(loc=μ,scale=σ,size=len(x))
data=pd.DataFrame({"Mediciones":x,"Observaciones":y})
## Estimación inicial
W1=W1
# Acumular resultados
w1=[]
train_loss=[]
# Número de veces que se cambian los parámetros
epochs=epochs
# Tasa de Aprendizaje
h=aprendizaje
#0.8
#print("Pérdidas:\n")
w1.append(W1)
train_loss.append(loss(W1,x,y))
#print(f"Condición Inicial: Pérdida: {loss(W1,x,y)}, Parámetro: {W1}\n")
for epoch in range(epochs):
W1=optimize(W1,x,y,h)
w1.append(W1)
losss=loss(W1,x,y)
train_loss.append(losss)
#if epoch%100==0:
#print(f"Iteración {epoch}: Pérdida: {losss}, Parámetro: {W1}")
# Haciendo el modelo
mod=w1[-1]*x
# eje β (par.)
β1x=onp.linspace(-11,16,epochs)
l=onp.empty(len(β1x))
for i in range(len(l)):
l[i]=((β1x[i]*x-y)**2).mean()
plt.figure(figsize=(22,7))
plt.subplot(121)
plt.plot(x,y,'o')
plt.plot(x,mod,'r--')
plt.xlabel("Mediciones",fontsize=15)
plt.ylabel("Observaciones",fontsize=15)
plt.legend(["Datos","Modelo"],fontsize=15)
plt.subplot(122)
plt.suptitle("Estimación de Parámetros",fontsize=20)
#ax = plt.axes()
plt.plot(β1x,l,'r--',lw=3) # Función de pérdida
plt.plot(w1,train_loss,'b--',lw=3,ms=8) # Ruta tomada por el optimizador
plt.plot(w1[0],train_loss[0],'ko',ms=8) # Condición Inicial
plt.plot(w1[-1],train_loss[-1],'go',ms=8) # Estado Final
plt.xlabel(r"$w_1$",fontsize=15)
plt.ylabel(r"Pérdida",fontsize=15)
plt.legend(["Función de Pérdida","Descenso del Gradiente","Estado Inicial","Estado Final"],fontsize=13)
plt.show()
interactive_plot = interactive(regresion, σ=(0, 10.), μ=(-3, 3, 0.5),m = (-10.,10.),epochs=(0,500),W1=(-10.,10.),aprendizaje=(0.0001,1.,0.01))
#output = interactive_plot.children[-1]
#output.layout.height = '350px'
interactive_plot
Ejercicios#
Hacer un aplicativo que muestre las animaciones de manera fluida.
Probar otro tipo de simulación de datos que no tengan tendencia lineal.
¿Cuáles son los hiperparámetros apropiados para obtener el mejor modelo en menos epochs?


