Análisis de correspondencias múltiples (ACM)#

Nota

Los trozos de código de esta página son de R. Por favor, ejecútelos en Colab o Binder

Fuente: Pardo CE (2020) Estadística descriptiva multivariada

Objetivos del ACM#

  • Describir las asociaciones entre las categorías de las variables activa.

  • Descubrir patrones de individuos, que pueden dar origen a grupos de ellos.

  • Sintetizar en imágenes geométricas (planos factoriales) las asociaciones entre categorías y los posibles grupos de individuos.

  • Explorar la explicación de la estructura inducida por las categorías activas, con variables que juegan el papel de ilustrativas.

Adicionalmente:

  • Cuantificar las variables cualitativas.

  • Reducir de dimensión.

  • Filtrar: conservar la información y eliminar el ruido.

El ACM es una extensión del ACS con propiedades muy particulares.

eigenvectores

Fuente: Statistical methods for archaeological data analysis I: Basic methods

Ejemplo: descripción de admitidos según algunas variables sociodemográficas, notación y transformaciones de datos#

  • Descripción de los 445 admitidos a la Facultad de Ciencias, para el semestre de 2013-I.

  • Datos disponibles en admi{FactoClass}

  • Se utilizan como variables activas las sociodemográficas disponibles:

    • Género: Femenino, Masculino

    • Edad: 16 o menos, 17, 18, 19 o más

    • Estrato: bajo, medio, alto

    • Procedencia: Bogotá, Cundinamarca, Otro

Notación#

  • La tabla de datos se denomina de código condensado (denotada por Y y no tiene significado numérico).

  • Las \(n\) filas representan a los individuos y

  • las \(s\) columnas a las variables cualitativas.

  • En el lenguaje de diseño de experimentos las columnas son factores

  • Las categorías son los niveles de los factores.

  • En R estas variables son de tipo factor.

Tabla de datos del ejemplo Admitidos#

Tabla de datos Y#

data(admi)
print("Names")
names(admi)

Y<-admi[,8:11] #tomamos las columnas genero, estrato, origen y edad
paste("Dimensión de Y:",dim(Y)[1],"x",dim(Y)[2])

Warning message in data(admi):
"data set 'admi' not found"

[1] "Names"

Error in eval(expr, envir, enclos): object 'admi' not found
Traceback:

# estracto de la tabla: múltiplo de 25
sel<-seq(25,425,25)
sel
Y[sel,]
  1. 25
  2. 50
  3. 75
  4. 100
  5. 125
  6. 150
  7. 175
  8. 200
  9. 225
  10. 250
  11. 275
  12. 300
  13. 325
  14. 350
  15. 375
  16. 400
  17. 425
A data.frame: 17 × 4
geneestrorigedad
<fct><fct><fct><fct>
25FmedioOtroa17
50Mbajo Bogoa18
75Mbajo Bogoa17
100MmedioBogoa18
125FmedioOtroa17
150Fbajo Bogoa16m
175Malto Bogoa19M
200Fbajo Otroa17
225Malto Otroa16m
250Malto Bogoa17
275Mbajo Bogoa17
300Mbajo Otroa19M
325Malto Bogoa17
350MmedioBogoa19M
375MmedioBogoa19M
400Fbajo Bogoa18
425Malto Bogoa16m

Tabla disyuntiva completa (TDC): Z #

Z<-acm.disjonctif(Y)
print("Dimensión de Z:")
dim(Z)
names(Z)<-substr(names(Z),6,8)

Z[sel,] #sel<-seq(25,425,25)
Y[sel[1:4],]
Z[sel[1:4],]

[1] "Dimensión de Z:"
  1. 445
  2. 12
A data.frame: 17 × 12
FMbajmedaltBogCunOtra16a17a18a19
<dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl>
25100100010100
50011001000010
75011001000100
100010101000010
125100100010100
150101001001000
175010011000001
200101000010100
225010010011000
250010011000100
275011001000100
300011000010001
325010011000100
350010101000001
375010101000001
400101001000010
425010011001000
A data.frame: 4 × 4
geneestrorigedad
<fct><fct><fct><fct>
25FmedioOtroa17
50Mbajo Bogoa18
75Mbajo Bogoa17
100MmedioBogoa18
A data.frame: 4 × 12
FMbajmedaltBogCunOtra16a17a18a19
<dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl>
25100100010100
50011001000010
75011001000100
100010101000010

  • La TDC Z es una yuxtaposición de s tablas, donde s es el número de variables: $\(\mathbf{Z}=[\mathbf{Z}_1 \ \mathbf{Z}_2 \ \cdots \mathbf{Z}_q \ \cdots \ \mathbf{Z}_s]\)$

  • Una variable cualitativa \(q\) \(\rightarrow\) Genera partición de los \(n\) individuos en \(p_q\) grupos, \(p_q\) = número de categorías de la variable \(q\).

  • En cada fila de \(\mathbf{Z}_q\) siempre hay un 1 y sólo un 1.

  • La suma en cada fila de \(\mathbf{Z}_q\) es de 1.

  • Como hay \(s\) submatrices \(\mathbf{Z}_q\), la suma de cada fila de \(\mathbf{Z}\) es \(s\), es decir que su marginal fila es un vector de \(n\) veces \(s\)

  • El total de Z es \(ns\).

  • En el ejemplo \(s=4\), \(n=445\) y el total de la tabla \(4*445=1780\).

  • La suma de cada columna de Z es el número de individuos que asumen la categoría \(j\) que se denota \(n_j\).

  • La \(\sum\limits_{j \in Z_q} n_j = n\). \(Z_q\) es el conjunto de categorías de la variable \(q\).

Tabla de Burt#

Z<-as.matrix(Z)
B<-t(Z)%*%Z
B
A matrix: 12 × 12 of type dbl
FMbajmedaltBogCunOtra16a17a18a19
F128 0 46 5923 89 930 46 4518 19
M 0317133126582222966 7212638 81
baj 46133179 0 0 952262 44 5822 55
med 59126 0185 01511123 47 7426 38
alt 23 58 0 081 65 511 27 39 8 7
Bog 89222 9515165311 0 0 7011647 78
Cun 9 29 22 11 5 038 0 9 19 2 8
Otr 30 66 62 2311 0 096 39 36 7 14
a16 46 72 44 4727 70 939118 0 0 0
a17 45126 58 74391161936 0171 0 0
a18 18 38 22 26 8 47 2 7 0 056 0
a19 19 81 55 38 7 78 814 0 0 0100
\[ \mathbf{B}=\mathbf{Z'}\mathbf{Z}\]

  • B es de orden \(p\times p\)

  • Se denota la yuxtaposición de tablas de contingencia cruzando todas las variables por parejas, como: $\(\mathbf{Z'}_q\mathbf{Z}_{q'}\)$

  • Bloque diagonal con matrices diagonales $\(\mathbf{Z'}_q\mathbf{Z}_{q} = diag(n_j), \ \ \ j \in J_q\)$

  • La matriz diagonal con los elementos diagonales de \(\mathbf{B}\) = suma de las columnas de Z: $\(\mathbf{D}_p = diag(n_j)\)$

# Matriz diagonal con elementos de la tabla de BURT (B)
Dp<-diag(diag(B))
Dp
A matrix: 12 × 12 of type dbl
128 0 0 0 0 0 0 0 0 0 0 0
0317 0 0 0 0 0 0 0 0 0 0
0 0179 0 0 0 0 0 0 0 0 0
0 0 0185 0 0 0 0 0 0 0 0
0 0 0 081 0 0 0 0 0 0 0
0 0 0 0 0311 0 0 0 0 0 0
0 0 0 0 0 038 0 0 0 0 0
0 0 0 0 0 0 096 0 0 0 0
0 0 0 0 0 0 0 0118 0 0 0
0 0 0 0 0 0 0 0 0171 0 0
0 0 0 0 0 0 0 0 0 056 0
0 0 0 0 0 0 0 0 0 0 0100

El ACM como un ACS de la TDC#

De ahora en adelante el término análisis de correspondencias simples (ACS) es sinónimo de análisis de correspondencias correspondencias (AC), entonces el ACM es el AC de la tabla disyuntiva completa (TDC) Z y escribimos \(AC(\mathbf{Z})\)

  • Tabla de frecuencias relativas: $\(\mathbf{F}=\dfrac{1}{ns}\mathbf{Z}\)$

  • Marginales fila: \(f_{i\cdot}=\dfrac{1}{n}; \forall i\)

  • Marginales columna: \(f_{\cdot j}=\dfrac{n_j}{ns}; \forall j\)

  • En el ejemplo: \(f_{i\cdot}=\dfrac{1}{445}=0.22\%; \forall i=1,\cdots,445\)

  • \(f_{\cdot j}~=~\dfrac{n_j}{445*4}~=\dfrac{n_j}{1780}; \forall j = 1,\cdots,12\),

  • Por ejemplo \(f_{\cdot 1}~=~\dfrac{128}{1780}=7.19\%\).

n<-nrow(Y) #numero de filas
s<-ncol(Y) #numero de columnas
F<-1/n*s*Z
round(head(F[sel,]),3)
A matrix: 6 × 12 of type dbl
FMbajmedaltBogCunOtra16a17a18a19
250.0090.0000.0000.00900.00000.0090.0000.0090.0000
500.0000.0090.0090.00000.00900.0000.0000.0000.0090
750.0000.0090.0090.00000.00900.0000.0000.0090.0000
1000.0000.0090.0000.00900.00900.0000.0000.0000.0090
1250.0090.0000.0000.00900.00000.0090.0000.0090.0000
1500.0090.0000.0090.00000.00900.0000.0090.0000.0000

Nube de Individuos#

Los \(n\) individuos conforman la nube \(N_n\) en \(\mathbb{R}^p\)

  • Coordenadas: filas de la tabla \(\dfrac{1}{s}\mathbf{Z}\): barras de altura \(1/s\) cuando el individuo asume la categoría \(j\) y 0 cuando no la asume.

  • Peso: \(\dfrac{1}{n}\)

  • Métrica: \(\mathbf{M}=ns \mathbf{D}_p^{-1}, \ \ \ \mathbf{D}_p = diag(n_j) \)

  • En el ejemplo: un perfil fila es \({\dfrac{1}{4} z_{ij}; j=1,\cdots,12}\),

  • con peso 0.22%.

  • Extracto de algunos perfiles

head(1/4*Z[sel,],4)
A matrix: 4 × 12 of type dbl
FMbajmedaltBogCunOtra16a17a18a19
250.250.000.000.2500.0000.2500.250.000
500.000.250.250.0000.2500.0000.000.250
750.000.250.250.0000.2500.0000.250.000
1000.000.250.000.2500.2500.0000.000.250

  • La métrica en este espacio de los individuos tiene término general \(m_j = \dfrac{1780}{n_j}\).

# Diagonal de la matriz de métrica
print("Names:")
colnames(Z)
print("Diagonal de la matriz de métrica:")
round(n*s*1/diag(Dp),1)

[1] "Names:"
  1. 'F'
  2. 'M'
  3. 'baj'
  4. 'med'
  5. 'alt'
  6. 'Bog'
  7. 'Cun'
  8. 'Otr'
  9. 'a16'
  10. 'a17'
  11. 'a18'
  12. 'a19'
[1] "Diagonal de la matriz de métrica:"
  1. 13.9
  2. 5.6
  3. 9.9
  4. 9.6
  5. 22
  6. 5.7
  7. 46.8
  8. 18.5
  9. 15.1
  10. 10.4
  11. 31.8
  12. 17.8

Centro de gravedad#

  • La coordenada \(j\) del centro de gravedad \(g_p\) es \(\dfrac{1}{n}\sum\limits_{i=1} ^n \dfrac{1}{s} z_{ij}=\dfrac{n_j}{ns} \), que es la marginal columna de \(\mathbf{F}=\dfrac{1}{ns}\mathbf{Z}\).

  • Para obtener el centro de gravedad, expresado en porcentaje, se puede de la siguiente manera:

round(colSums(1/n/s*Z)*100,1)
F
7.2
M
17.8
baj
10.1
med
10.4
alt
4.6
Bog
17.5
Cun
2.1
Otr
5.4
a16
6.6
a17
9.6
a18
3.1
a19
5.6

Distancia entre individuos#

\[ d^2(i,l)=ns\sum_{j=1}^p \frac{1}{n_j} \left(\dfrac{1}{s}\left[ z_{ij}-z_{lj} \right] \right)^2= \frac{n}{s} \sum_{j=1}^p \frac{1}{n_j} \left(z_{ij}-z_{lj} \right)^2 \]

  • Si dos individuos se parecen = asumen más o menos las mismas categorías.

  • La distancia se amplifica más cuando uno solo de los dos individuos asume una categoría de baja frecuencia.

  • Por ejemplo la distancia al cuadrado entre los individuos 50 y 100 es \(d^2(i50,i100)= \dfrac{445}{4}\left(\dfrac{1}{179}+\dfrac{1}{185}\right)=1.22\) y la diferencia entre ellos en estrato bajo y medio:

Y[c(50,100),]
A data.frame: 2 × 4
geneestrorigedad
<fct><fct><fct><fct>
50Mbajo Bogoa18
100MmedioBogoa18

Inercia de la nube de perfiles fila#

\[ \dfrac{1}{n} \sum\limits_{i=1}^n d^2(i,\mathbf{g}_p) = \dfrac{1}{n} \sum\limits_{i=1}^n \sum\limits_{j=1}^p \dfrac{ns}{n_j}(\dfrac{z_{ij}}{s}-\dfrac{n_j}{ns})^2= \dfrac{1}{s} \sum\limits_{j=1}^p \dfrac{1}{n_j} \sum\limits_{i=1}^n (z_{ij}^2 -2 z_{ij} \dfrac{n_j}{n} + \dfrac{n_j^2}{n^2}) = \]
\[ \dfrac{1}{s} (p - 2 s + s) = \dfrac{p}{s} - 1 \]

  • La inercia de la nube de puntos depende del cociente entre el número de categorías y el número de variables, no de los valores internos de la tabla, por lo tanto no tiene significado estadístico.

  • En el ejemplo es \(12/4 -1 = 2\).

Eje y subespacios vectoriales#

\[ AC(Z) = ACP\left(\dfrac{1}{s}\mathbf{Z},ns\mathbf{D}_p^{-1},\dfrac{1}{n}\mathbf{I}_n\right) \]

  • La matriz de inercia es: $\( \dfrac{1}{s}\mathbf{Z'}\dfrac{1}{n}\mathbf{I}_n\dfrac{1}{s}\mathbf{Z}ns\mathbf{D}_p^{-1}= \dfrac{1}{s}\mathbf{Z'Z}\mathbf{D}_p^{-1}= \dfrac{1}{s}\mathbf{B}\mathbf{D}_p^{-1} \)$

  • El rango de esta matriz es igual al rango de Z, que es \(p-s\), porque por cada variable hay una columna que es linealmente dependiente,

  • Una columna se puede obtener como la diferencia entre el vector de \(n\) unos y la suma de las demás columnas asociadas a la variable.

  • La nube de puntos está soportada en un subespacio de dimensión \(p-s\), que es el número de valores propios mayores que cero.

  • En el ejemplo hay \(12-4=8\) valores propios mayores que cero,

Valores propios del ACM de admitidos#

acm<-dudi.acm(Y,scannf=FALSE,nf=3)
inertia(acm)
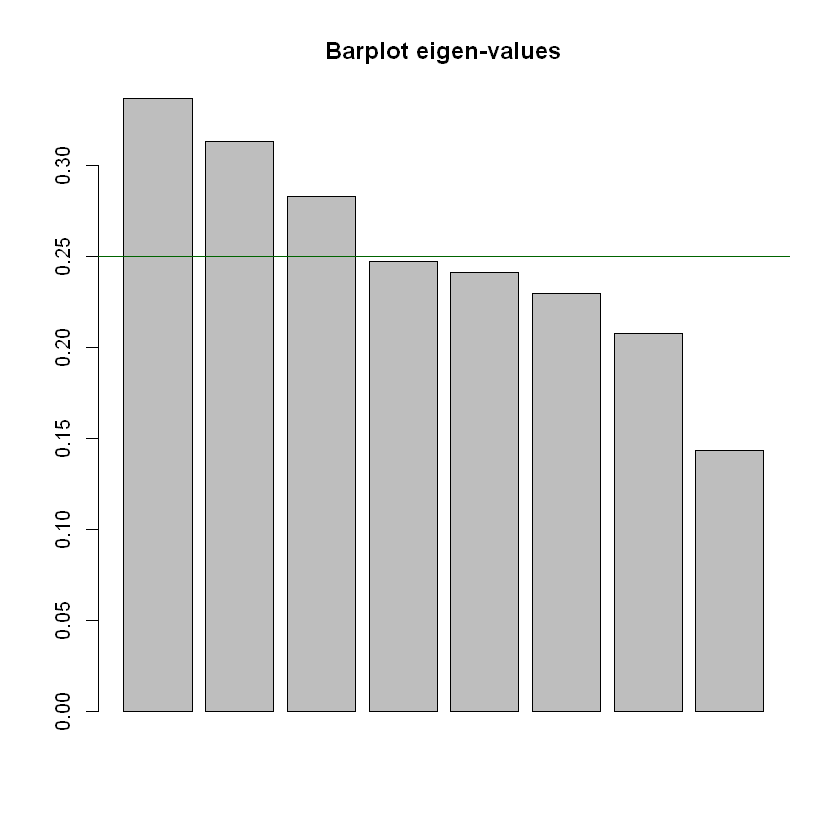
barplot(acm$eig,main="Barplot eigen-values")
abline(h=sum(acm$eig)/8,col="darkgreen")

Inertia information:
Call: inertia.dudi(x = acm)

Decomposition of total inertia:
    inertia     cum  cum(%)
Ax1  0.3366  0.3366   16.83
Ax2  0.3128  0.6493   32.47
Ax3  0.2827  0.9320   46.60
Ax4  0.2471  1.1791   58.96
Ax5  0.2408  1.4199   71.00
Ax6  0.2293  1.6493   82.46
Ax7  0.2075  1.8568   92.84
Ax8  0.1432  2.0000  100.00
../../_images/ACM_40_1.png

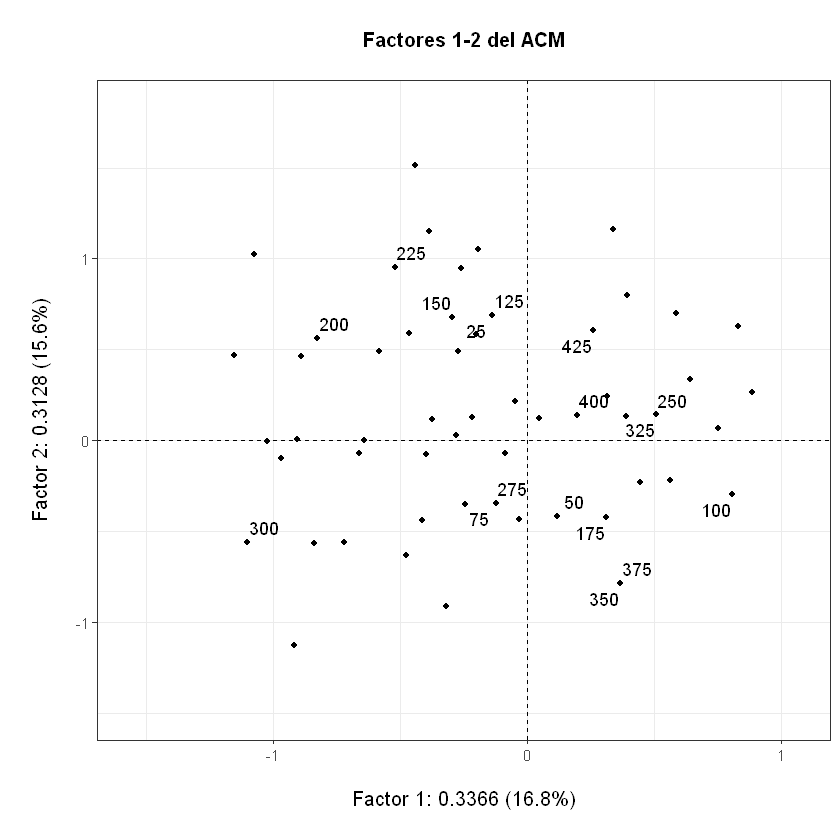
Primer plano factorial del ACM de admitidos#

plot(acm,Tcol=FALSE,gg=TRUE,roweti=sel,main="Factores 1-2 del ACM")
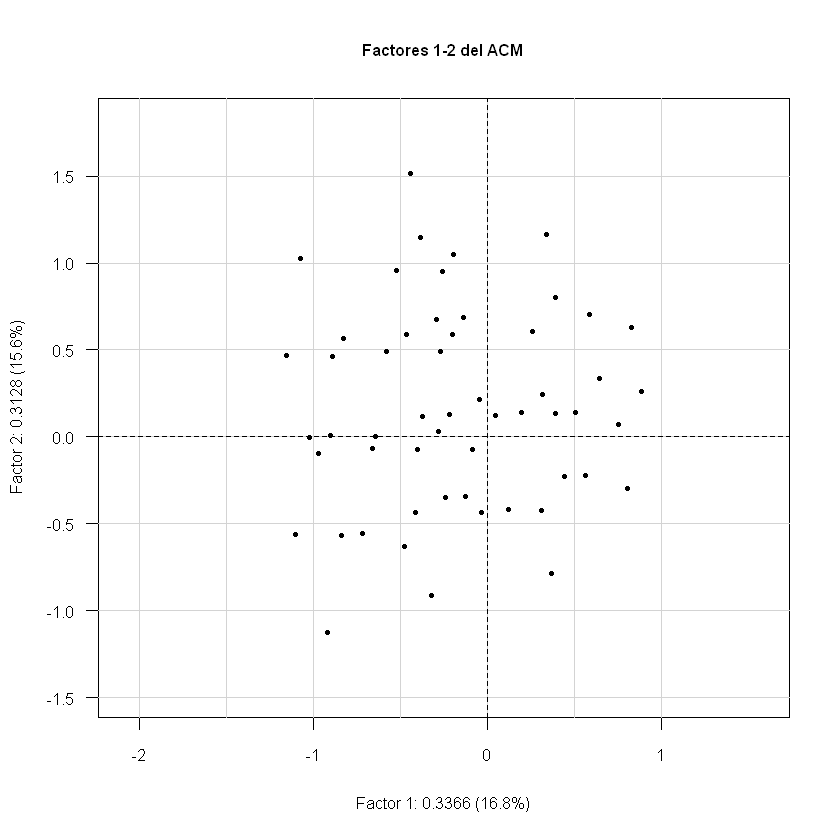
plot(acm,Tcol=FALSE,ucal=1.0,asp=1,main="Factores 1-2 del ACM")
../../_images/ACM_42_0.png ../../_images/ACM_42_1.png

Nube de categorías#

Coordenadas: Columnas de la tabla \(\mathbf{ZD}^{-1}_p\)#

  • Cada perfil columna \(j\) tiene solo dos alturas: cero o \(1/n_j\).

  • Las alturas son en general, diferentes en cada perfil.

  • El peso de cada categoría es \(\dfrac{n_j}{ns}\)

Centro de gravedad: Es el vector de \(n\) valores \(\dfrac{1}{n}\)#

  • Coordenada \(i\) del centro de gravedad: $\( \mathbf{g}(i) = \sum_{j=1}^p \frac{n_j}{ns} \frac{z_{ij}}{n_j} = \sum_{j=1}^p \frac{1}{ns} z_{ij} = \frac{1}{ns} s = \frac{1}{n} \)$

Métrica: \(n \mathbf{I}_n\)#

Distancia entre dos categorías#

\[ d^2(j,k) = \sum_{i=1}^n n \left(\frac{z_{ij}}{n_j} - \frac{z_{ik}}{n_k}\right)^2 \]

Interpretación de la distancia entre categorías#

                   Categoría k  
           
                 |   1  |  0   | suma
                 --------------------  
  Categoria   1  |   a  |  b   | n_j

     j        0  |   c  |  d   | c+d
                 -------------------- 
          suma   |  n_k | b+d  |  n
\[ d^2(j,k) = n \left( \frac{n_k + n_j - 2a}{n_j n_k} \right) = n \left( \frac{a+c+a+b - 2a}{n_j n_k} \right) = \frac{n}{n_j n_k} (b+c) \]

  • En la distancia de dos categorías, sólo se suman los individuos que asumen una y solo una de las dos categorías.

  • Las categorías de baja frecuencia se alejan más de las demás.

Contribución de categorías y variables a la inercia #

  • Distancia entre la categoría \(j\) y el centro de gravedad \(\mathbf{g}_n=\dfrac{1}{n}\mathbf{1}_n\):

\[ d^2(j,\mathbf{g}_n) = n \sum_{i=1}^{n} \left( \frac{z_{ij}}{n_j} - \frac{1}{n} \right)^2 = n \sum_{i=1}^n \left(\frac{z_{ij}^2}{n_j^2}-2 \frac{z_{ij}}{n_j} \frac{1}{n} + \frac{1}{n^2}\right)= \frac{n}{n_j} - 1 \]

  • Las categorías de menos frecuencia son las más alejadas del origen

\[ I(N_p) =\sum_{q=1}^s \sum_{j \in J_q} \frac{n_j}{ns} d^2(j,\mathbf{g}_n) = \sum_{q=1}^s \sum_{j \in J_q} \frac{n_j}{ns} \left(\frac{n}{n_j}-1\right) = \sum_{q=1}^s \sum_{j \in J_q} \frac{1}{s} \left(1-\frac{n_j}{n}\right) \]

  • \(J_q\) es el conjunto de categorías que pertenecen la variable \(q\).

Contribuciones a la inercia#

  • De una categoría \(j\): \( \dfrac{1}{s}\left(1-\dfrac{n_j}{n}\right) \), contribuyen más las categorías de baja frecuencia.

  • De una variable \(q\): \(\sum\limits_{j \in J_q} \dfrac{1}{s} \left(1-\dfrac{n_j}{n}\right) = \dfrac{1}{s}\left(p_q-\dfrac{n}{n}\right) = \dfrac{1}{s}\left(p_q-1\right)\), contribuyen más las variables con más categorías

  • Inercia total: \(\sum\limits_{q=1}^s \dfrac{1}{s}\left(p_q-1\right) = \dfrac{1}{s}(p-s) =\dfrac{p}{s}-1\). No tiene significado estadístico, no depende de los valores de la tabla sino de la relación entre número de categorías y número de variables.

Subespacio de proyección de las categorías#

Primer plano Factorial#

plot(acm,Trow=FALSE,gg=TRUE,main="Factores 1-2")

Error in plot(acm, Trow = FALSE, gg = TRUE, main = "Factores 1-2"): object 'acm' not found
Traceback:

1. plot(acm, Trow = FALSE, gg = TRUE, main = "Factores 1-2")

Coordenadas y ayudas para la interpretación de las categorías para los tres primeros ejes#

ayuacm<-inertia(acm,,T)
names(ayuacm)
round(cbind(acm$co,ayuacm$col.abs,ayuacm$col.rel,ayuacm$col.contrib),2)
round(sum(acm$eig)/12*100,2)

Error in inertia(acm, , T): object 'acm' not found
Traceback:

1. inertia(acm, , T)

El ACM como un ACP(X,M,N) de la TDC)#

\[ ACP(\mathbf{X,M,N}) \]

  • \(\mathbf{X}= n \mathbf{I}_n\dfrac{1}{ns}\mathbf{Z} ns \mathbf{D}=n\mathbf{ZD}_p^{-1}\),

    • término general: \(x_{ij}=\dfrac{n}{n_j} z_{ij}\).

  • \(\mathbf{M}=\dfrac{1}{ns}\mathbf{D}_p\),

    • término general: \(m_j = \dfrac{n_j}{ns}\).

  • \(\mathbf{N}=\dfrac{1}{n}\mathbf{I}_n\),

    • término general: \(d_i=\dfrac{1}{n}\).

M - distancia al cuadrado entre dos individuos \(i\) y \(l\)#

\[ d^2(i,l) = \sum_{j=1}^p \dfrac{n_j}{ns} \left(\dfrac{n}{n_j} z_{ij}-\dfrac{n}{n_j} z_{lj} \right)^2 = \dfrac{n}{s} \sum_{j=1}^p \dfrac{1}{n_j} (z_{ij} - z_{lj})^2 \]

N - distancia al cuadrado entre dos categorías#

\(j\) y \(k\) de X $\( d^2(j,k)= \sum_{i=1}^n \frac{1}{n}\left(\dfrac{n}{n_j} z_{ij}-\dfrac{n}{n_k} z_{ik} \right)^2 = n \sum_{i=1}^n \left(\dfrac{z_{ij}}{n_j} -\dfrac{z_{ik}}{n_k} \right)^2 \)$

Relaciones cuasibaricéntricas#

Coordenada de una individuo en función de las coordenadas de las categorías#

\[ F_s(i) = \frac{1}{\sqrt{\lambda_s}} \frac{1}{s} \sum_{j=1}^p z_{ij} G_s(j) = \frac{1}{\sqrt{\lambda_s}} \frac{1}{s} \sum_{j \in J_i} G_s(j) \]

  • \(J_i\) es el conjunto de categorías que son asumidas por el individuo \(i\).

  • La coordenada sobre un eje \(s\) del individuo \(i\) se sitúa en el promedio aritmético de las coordenadas de las categorías que asume, dilatadas por el inverso de la raíz cuadrada del valor propio.

  • Ejemplo: el primer individuo de la tabla asume las categorías:

    • Ge.F (0.1) es la coordenada sobre el primer eje, Ed.17 (0.2), Es.medio (0.7) y - Or.Otro (-1.3).

    • Promedio aritmético: (0.1+0.2+0.7-1.3)/4 = -0.08.

    • La dilatación es \(1/\sqrt{0.337}=1.72\).

    • La coordenada es 1.72*(~-0.08) = -0.14.

Coordenada de una categoría en función de las coordenadas de los individuos #

\[ G_s(j) = \frac{1}{\sqrt{\lambda_s}} \frac{1}{n_j} \sum_{i=1}^n z_{ij} F_s(i) \]

  • \(I_j\) es el conjunto de individuos que asumen la categoría \(j\),

    • La categoría \(j\) se sitúa en el promedio aritmético de las coordenadas de los individuos que la asumen, dilatada por el inverso de la raíz cuadrada del valor propio.

Representación simultánea en el primer plano factorial#

plot(acm,roweti="",main="Representación simultanea 1er plano")
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

Plano factorial 2-3#

plot(acm,2,3,roweti="",main="Representación simultanea factores 2-3")
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

Razones de correlación sobre un eje de las variables cualitativas#

  • Una variable cualitativa induce una partición de los \(n\) individuos y la inercia (varianza) de los individuos sobre el eje se puede descomponer en \(varianza \ inter + varianza \ intra\).

Varianza inter e intra

  • La razón de correlación se define como el cociente entre varianza inter y varianza total.

  • La varianza total de \(F_s\) es \(\lambda_s\),

  • La varianza inter con respecto a una variable \(q\) es: $\( \sum_{j \in J_q} \frac{n_j}{n} (\overline{F}_{sj})^2 \)\( puesto que las coordenadas sobre \)s\( están centradas. donde \)\overline{F}{sj} = \sum\limits{i \in I_{j \in J_q}} \frac{1}{n_j} F_{s}(i)\(, es decir, el promedio aritmético de las coordenadas sobre el eje \)s\( de los individuos que asumen la categoría \)j\( de la variable \)q$.

  • Por las relaciones de transición \(\overline{F}_{sj} = \sqrt{\lambda_s} G_s(j)\), entonces: $\( Varianza \ entre (q) = \lambda_s \ \sum_{i \in J_q} \frac{n_j}{n} G_s^2(j) \)\( y la razón de correlación es: \)\( \eta^2_s(q) = \sum_{j \in J_q} \frac{n_j}{n} G_s^2(j) \)$

  • Se puede expresar como función de la contribución absoluta de las categorías como: $\( \eta^2_s(q) = \lambda_s s \sum_{j \in q_j} Ca_s(j) \)\( donde \)J_q\( es el conjunto de categorías de la variable \)q\( y \)Ca_s(j)\( es la contribución absoluta de la categoría \)j\( sobre el eje \)s$.

  • Estos valores se encuentran en el objeto de salida de la función dudi.acm{ade4}, en la tabla cr.

  • Con estas razones de correlación se pueden obtener los planos factoriales para las variables cualitativas.

  • Por ejemplo para la variable \(Origen\), la suma de las contribuciones de las tres categorías sobre el primer eje es \(13.45+4.87+27.18=45.5\%\), el primer valor propio es \(0.3366\) y el número de variables \(4\),

  • La razón de correlación es \(\eta^2_1(Origen)=4*0.3366*0.455=0.613\), valor que se puede leer en la figura siguiente.

plotfp(acm$cr,main="Factores 1-2, radios de correlación") # función de FactoClass
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346
 
plotfp(acm$cr,2,3,main="Factores 2-3, radios de correlación")
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

Elementos suplementarios#

Individuos Suplementarios#

  • Los individuos ilustrativos se pueden proyectar utilizando la fórmula cuasibaricéntrica.

  • La coordenada de un individuo suplementario es el promedio de las coordenadas de las categorías que asume, dilatado por el inverso de la raíz cuadrada del valor propio.

Variables cualitativas suplementarias#

  • Las categorías de una variable ilustrativa se proyectan mediante la fórmula cuasibaricéntrica

  • Como el promedio de las coordenadas de los individuos que la asumen, dilatado por el inverso de la raíz cuadrada del valor propio.

  • Se pueden calcular sus cosenos cuadrados sobre los ejes.

  • Valores test.

Valores test para categorías suplementarias#

  • Una categoría \(j\) es asumida por los \(n_j\) individuos del conjunto \(I_j\),

  • Su coordenada, sobre un eje \(s\) es el promedio aritmético de las coordenadas de esos individuos sobre el eje, multiplicada por el inverso de la raíz cuadrada del valor propio \(\lambda_s\).

  • Si se supone que los \(n_j\) individuos se extraen al azar de los \(n\) individuos:

    • La media de las coordenadas es 0 y su varianza es \(\left( \dfrac{n-n_j}{n-1} \right) \dfrac{\lambda_s}{n_j}\).

    • La varianza de la categoría \(j\) se obtiene multiplicando la varianza anterior por \(\dfrac{1}{\lambda_s}\):
      $\(\dfrac{1}{\lambda_s} \left( \dfrac{n-n_j}{n-1} \right) \dfrac{\lambda_s}{n_j} = \dfrac{n-n_j}{n(n-1)} \)$

    • El valor calculado de la estadística \(T\) para la verdadera coordenada es: $\( t_s(j) = \sqrt{\dfrac{n_j(n-1)}{n-n_j}} G_s(j) \)$

Ejemplo#

Valor test para Química sobre el primer eje:#

# Número de admitidos por carreras:
summary(admi$carr)
# Valor test:
vtQui = sqrt(63*(445-1)/(445-63))*(-0.259)
round(vtQui,3)
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

  • La diferencia con el valor de la salida se debe al número de cifras significativas.

  • Este valor, menor que -2, indica que es válido leer la posición negativa de Química sobre el primer eje, lo que significa que está asociada con estrato bajo y origen fuera de Bogotá.

Carreras sobre el primer plano factorial del ACM de admitidos#

supCarr<-supqual(acm,admi$carr)
names(supCarr)
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346
 
attach(supCarr)
"Coordenadas y ayudas para la interpretación"
cbind(ncat,round(cbind(dis2,coor,tv,cos2),3))
"Razones de correlación"
round(scr*100,2)
detach(supCarr)
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

  • Sólo es legítimo interpretar como diferente de cero las coordenadas de:

  • Química (-) sobre el primer eje, Matemáticas (+) sobre el segundo eje; y Geología (-) opuesto a Farmacia (+) sobre el tercer eje.

  • Química tiene, en comparación al promedio, mayor proporción de admitidos de estrato bajo y origen fuera de Bogotá,

  • Matemáticas de 19 o más años,

  • Geología de 17 años y de estrato alto,

  • Farmacia de 18 años y género femenino.

Proyección de las carreras sobre el primer plano factorial#

plot(acm,Trow =FALSE,infaxes="no",main="Plano 1-2",
ylim =c( -1.5 ,1.3) , col.col=" black ")
points( supCarr$coor ,col ="darkgreen")
text(supCarr$coor , labels = attributes (admi[,1])$levels ,
col ="darkgreen",pos =1, cex =0.8 , font =3)
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

Proyección de las carreras sobre el plano factorial 2-3#

plot(acm,2,3,Trow =FALSE,infaxes="no",main="Plano 2-3",
ylim =c( -1.5 ,1.3) , col.col=" black ")
points(supCarr$coor[,c(2,3)] ,col ="darkgreen")
text(supCarr$coor[,c(2,3)] , labels = attributes (admi[,1])$levels ,
col ="darkgreen",pos =1, cex =0.8 , font =3)
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

Retorno a los datos#

Perfiles fila de las carreras según las variables activas, para corroborar lo que se ve en los planos factoriales

par(mfrow=c(2,2))
for (varac in 8:11){
    K<-unclass(table(admi$carr,admi[,varac]))
    plotct(K,"row",col=2:5,main=colnames(admi)[varac])
}
A data.frame: 3 × 3
CS1CS2CS3
<dbl><dbl><dbl>
Color0.579-0.571 0.581
DA0.673-0.067-0.737
EA0.460 0.818 0.346

  • Química tiene, en comparación al promedio, mayor proporción de admitidos de estrato bajo y origen fuera de Bogotá,

  • Matemáticas tiene mayor proporción de admitidos de 19 o más años,

  • Geología tiene mayor proporción de admitidos de 17 años y de estrato alto,

  • Farmacia tiene mayor proporción de admitidos de 18 años y género femenino.

Para más detalles del ACM y un ejemplo de aplicación ver el capítulo 6 del libro EDM.