Algunos métodos de clasificación no supervisada (agrupamiento)
Contents
Algunos métodos de clasificación no supervisada (agrupamiento)#
Cuidado
Los trozos de código de esta página son de R. Por favor, ejecútelos en Colab
Fuente: Pardo CE (2020) Estadística descriptiva multivariada
Objetivos de los métodos de agrupamiento#
Objetivo: Descubrir patrones en los datos en forma de grupos bien diferenciados, que tengan individuos homogéneos en su interior.
En inglés: Cluster Analysis (análisis de conglomerados)
Métodos de clasificación no supervisada: en las áreas de minería de datos, aprendizaje automático y reconocimiento de patrones.
En el sentido matemático un algoritmo de agrupamiento busca una partición de un conjunto de \(n\) elementos en \(K\) subconjuntos,
Equivale a definir una variable cualitativa que emerge de los datos.
Tipos de métodos#
Los que permiten obtener una partición directa mediante un algoritmo, el más conocido y utilizado es el K-means.
Los que construyen una sucesión de particiones anidadas, que se representan mediante un árbol o dendrograma, se conocen como métodos de clasificación jerárquica.
Clasificación jerárquica aglomerativa: parten de todos los individuos, como n clases de un elemento y los van uniendo en pasos sucesivos hasta llegar a un solo grupo o clase de n individuos.
Clasificación jerárquica divisiva.
Los algoritmos de clasificación requieren de medidas de similitud, disimilitud o distancia entre individuos y entre grupos.
Las similitudes, disimilitudes o distancias entre grupos constituyen los criterios de agregación de los métodos de clasificación jerárquica aglomerativa.
Combinar los dos tipos de métodos de clasificación.

Fuente: quatdare
Métodos para obtener una partición directa#
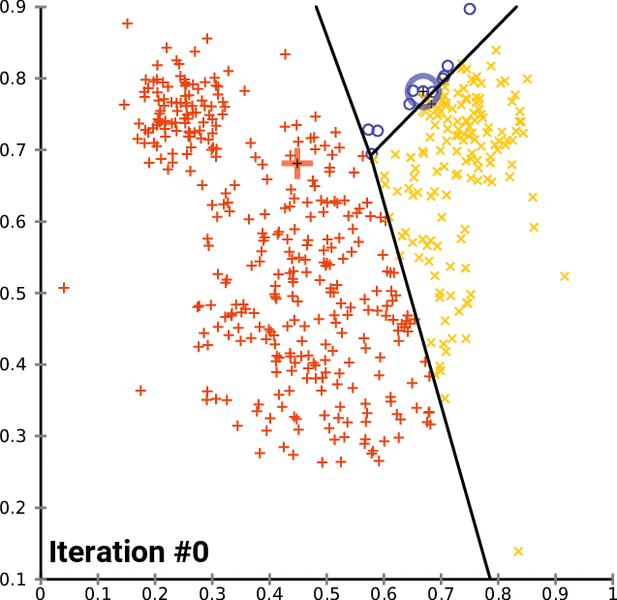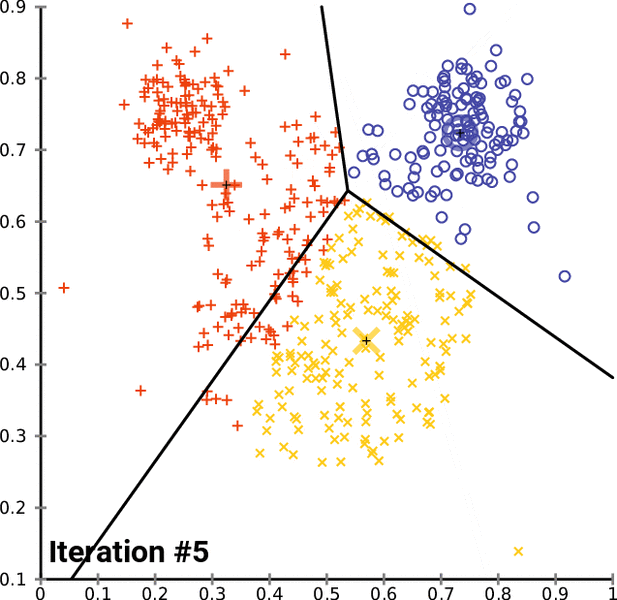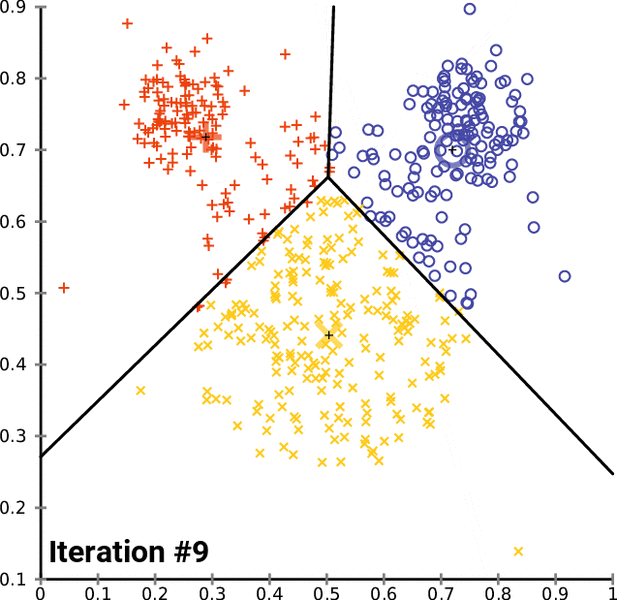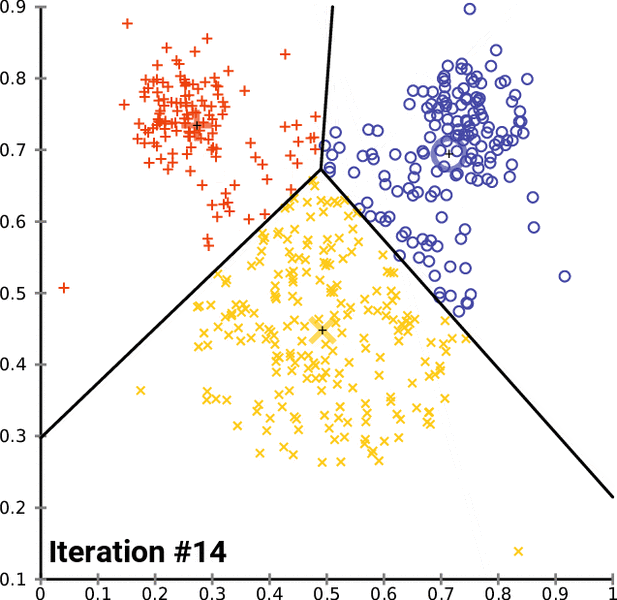
K-means#
Se da el número de clases, los puntos iniciales requeridos para empezar el algoritmo y un criterio de parada.
Está relacionado con la geometría utilizada en los métodos en ejes principales porque recurre a la distancia Euclidiana entre individuos.
La distancia entre grupos se calcula como la distancia Euclidiana entre sus centros de gravedad.
Homogeneidad intra grupos: inercia intra.
Heterogeneidad entre grupos: inercia entre.
Inercia = inercia intra + inercia entre.
Fuente: Wikipedia
Descomposición de la inercia asociada a una partición#
Sea una nube de \(n\) puntos \(N_n\) en \(\mathbf{p}\) con una partición en \(K\) clases. $\( Inercia(N_n)=\sum_{i=1}^n p_i d^2(i,\mathbf{g}) = \sum_{k=1}^K p_k d^2(\mathbf{g}_k,\mathbf{g}) + \sum_{k=1}^K \sum_{i \in I_k } p_id^2(i,\mathbf{g}_k) \)$
\(p_i\): peso del individuo \(i\), \(\sum\limits_{i=1}^n p_i = 1\)
\(\mathbf{g}\): centro de gravedad de la nube de puntos, \(\mathbf{g}=\sum\limits_{i=1}^n p_i \mathbf{x}_i\), \(\mathbf{x'}_i\), es la fila \(i\) de la matriz de coordenadas de los puntos \(\mathbf{X}\) con \(n\) filas y \(p\) columnas.
\(p_k\) peso de la clase \(k\), \(p_k = \sum\limits_{i \in I_k } p_i\)
\(\mathbf{g}_k\): centro de gravedad de la clase \(k\), \(\mathbf{g}_k = \dfrac{1}{p_k}\sum\limits_{i \in I_k } p_i \mathbf{x}_i\)
\(d^2(.,.)\)] es la distancia Euclidiana canónica.
En el cálculo de la inercia ha intervenido la distancia Euclidiana canónica, entonces la medida de disimilitud entre individuos ya está seleccionada.
El método K-means busca una partición en \(K\) clases que tenga inercia intra-clases mínima.
El algoritmo \(K-means\)#
Paso 0
\(K\) centros iniciales de las clases: \(\{C^{0}_{1}, C^{0}_{2},\ldots,C^{0}_{k},\ldots,C^{0}_{K}\}\)
Partición 0 \(P^0=\{ I^{0}_{1}, I^{0}_{2},\ldots, I^{0}_{k},\ldots,I^{0}_{K}\}\).
El individuo \(i\) pertenece a la clase \(I^0_k\) si el punto \(i\) está más próximo de \(C^0_k\) que de todos los demás centros.
Paso 1
De las clases \(\{ I^{0}_{1}, I^{0}_{2},\ldots, I^{0}_{k},\ldots,I^{0}_{K}\}\)
\(K\) centros de gravedad \(\{C^{1}_{1},C^{1}_{2},\ldots,C^{1}_{k},\ldots,C^{1}_{K}\}\)
Partición 1: \(P^1=\{ I^{1}_{1}, I^{1}_{2},\ldots, I^{1}_{k},\ldots,I^{1}_{K}\}\)
Paso \(m\)
De las clases \(\{ I^{m-1}_{1}, I^{m-1}_{2},\ldots,I^{m-1}_{k},\ldots,I^{m-1}_{K}\}\)
\(K\) nuevos centros \(\{C^{m}_{1}, C^{m}_{2},\ldots,C^{m}_{k},\ldots,C^{m}_{K}\}\)
Partición \(m\): \(P^m=\{ I^{m}_{1}, I^{m}_{2},\ldots,I^{m}_{k},\ldots,I^{m}_{K}\}\) . El algoritmo se detiene si la nueva partición no es mejor que la anterior (la varianza intra-clases deja de disminuir)
Generalmente la partición obtenida depende de la selección inicial de los centros.
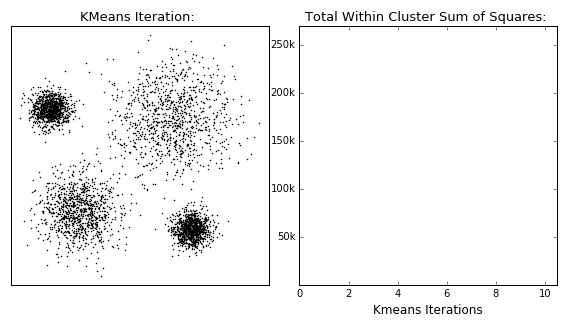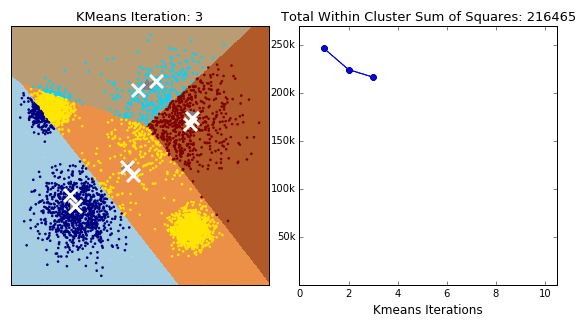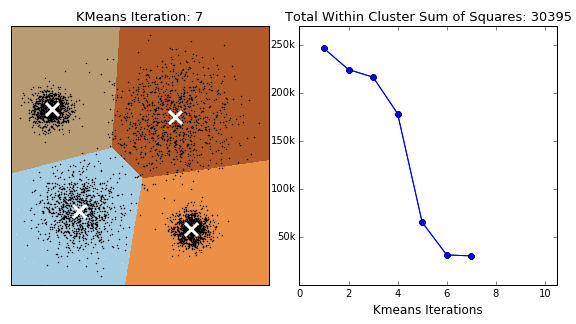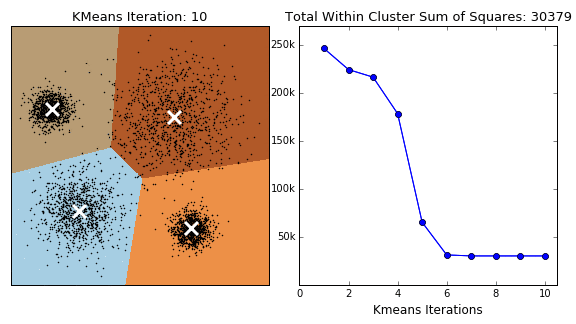
Fuente: David Sheehan
El algoritmo K-means disminuye la inercia intra-clases#
Hay que demostrar que la inercia intra-clases de la partición \(P^{m}=\{ I^{m}_{1}, I^{m}_{2},\ldots,I^{m}_{k},\ldots,I^{m}_{K}\}\) es menor o igual a la inercia intra-clases de la partición \(P^{m-1}\)
A cada individuo del conjunto a clasificar, se le asocia un peso \(p_i>0\) tal que \(\sum\limits_{i=1}^np_i=1\).
\(d^2(i,C^m_k)\) es el cuadrado de la distancia entre el individuo \(i\) y el centro móvil de la clase \(k\) en la etapa \(m\) , que es el centro de gravedad de la clase \(k\) en el paso \(m{-}1\).
Entonces, la suma de las inercias de las clases de la partición \(P^m\) con respecto a los puntos que permitieron construirla es
$\( v(m)=\sum\limits_{k=1}^K \sum_{i \in I_k^m } p_i d^2(i,C_k^m) \)$
En la etapa \(m\), \(I_k^m\) es el conjunto de los individuos que están más próximos a \(C_k^m\) que de todos los otros centros
El centro de gravedad de esta clase se calcula en la etapa \(m+1\): \(C_k^{m+1}=\mathbf{g}_k^m\).
La inercia intra-clases en la etapa \(m\) es la cantidad $\( V(m)= \sum_{k=1}^K \sum_{i \in I_k^m } p_id^2(i,\mathbf{g}_k^{m}) =\sum_{k=1}^K \sum_{i \in I_k^m } p_id^2(i,C_k^{m+1}) \)$
\(C_k^{m+1}\) es el centro de gravedad de la clase \(I_k^m\), que es el nuevo centro móvil en la etapa \(m+1\).
\(V(m)\) es menor o igual que \(v(m)\) porque la inercia con respecto al centro de gravedad es siempre menor o igual a la inercia con respecto a cualquier otro punto.
La suma de las inercias con respecto a los puntos que originaron la partición \(P^{m+1}\) es
$\( \textbf{v}(m+1)=\sum_{k=1}^K \sum_{i \in I_k^{m+1} } p_id^2(i,C_k^{m+1}) \)$\(v(m+1)\) es menor o igual a \(V(m)\) porque si al menos un individuo cambia de clase en la nueva partición es porque queda más cerca de otro nuevo centro.
Entonces \(v(m+1)\leq V(m) \leq v(m) \leq V(m-1)\), es decir que la inercia intra-clases disminuye con cada paso del algoritmo.
Ejemplo de «juguete»: \(K{-}means\) ejemplo Café#
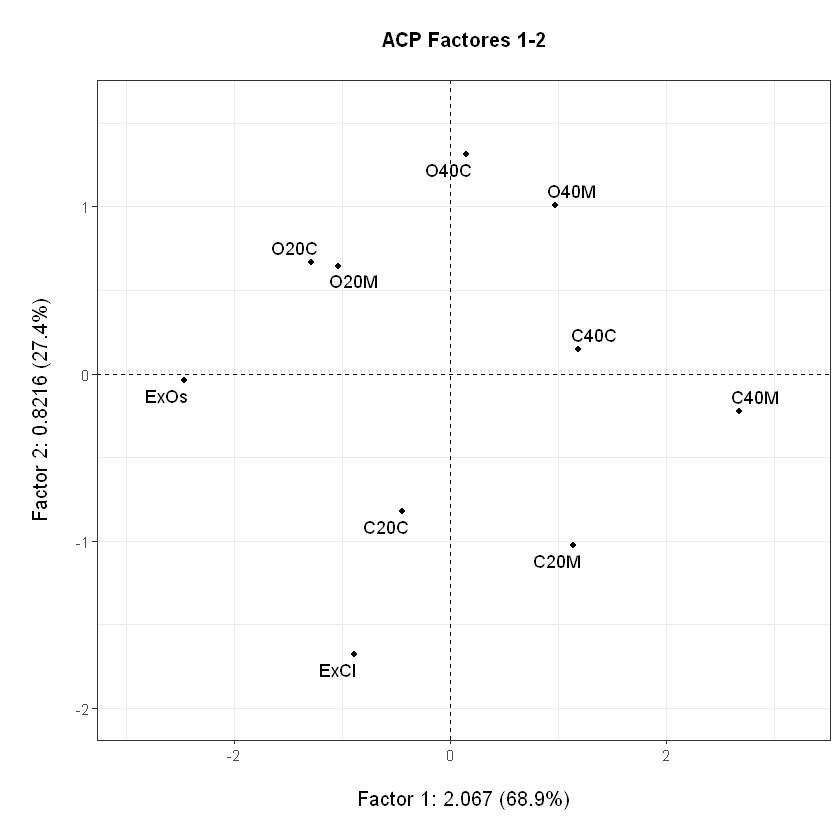
Tomando el ejemplo de Café, partiendo de las coordenadas sobre el primer plano factorial del ACP normado de las tres variables físicas, y tomando como centros iniciales los cafés ExCl y O40C.
Primer plano factorial y coordenadas#
# Instalación de FactoClass:
#install.packages("FactoClass")
library(FactoClass)
data(cafe)
acp<-dudi.pca(cafe[1:10,1:3],scannf=FALSE)
plot(acp,Tcol=FALSE,gg=TRUE,main="ACP Factores 1-2")
F<-as.matrix(round(acp$li,2))
t(F)
Loading required package: ade4
Loading required package: ggplot2
Loading required package: ggrepel
Loading required package: xtable
Loading required package: scatterplot3d
| ExCl | C40M | C40C | C20M | C20C | ExOs | O40M | O40C | O20M | O20C | |
|---|---|---|---|---|---|---|---|---|---|---|
| Axis1 | -0.89 | 2.68 | 1.18 | 1.14 | -0.44 | -2.47 | 0.98 | 0.15 | -1.04 | -1.29 |
| Axis2 | -1.68 | -0.22 | 0.15 | -1.02 | -0.82 | -0.04 | 1.01 | 1.31 | 0.65 | 0.67 |
Paso 0#
Puntos iniciales: ExCl y O40C
tab<-NULL# para para registrar los pasos 3 filas DC1, DC2, Partición
cen <- NULL# matriz para recoger los centros de cada paso, por columnas
"Centros iniciales"
C<-F[c(1,8),];rownames(C)<-c("C1","C2");C
"Distancias a los centros iniciales"
as.matrix(dist(rbind(F,C)))[11:12,1:10]->D;round(D,2)
"Partición"
factor(D[1,]>D[2,],labels=c("I1","I2"))->P; t(data.frame(P))
cen<-C
tab<-rbind(D,P);round(tab,2)
| Axis1 | Axis2 | |
|---|---|---|
| C1 | -0.89 | -1.68 |
| C2 | 0.15 | 1.31 |
| ExCl | C40M | C40C | C20M | C20C | ExOs | O40M | O40C | O20M | O20C | |
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.00 | 3.86 | 2.76 | 2.13 | 0.97 | 2.28 | 3.28 | 3.17 | 2.33 | 2.38 |
| C2 | 3.17 | 2.96 | 1.55 | 2.53 | 2.21 | 2.95 | 0.88 | 0.00 | 1.36 | 1.58 |
| ExCl | C40M | C40C | C20M | C20C | ExOs | O40M | O40C | O20M | O20C | |
|---|---|---|---|---|---|---|---|---|---|---|
| P | I1 | I2 | I2 | I1 | I1 | I1 | I2 | I2 | I2 | I2 |
| ExCl | C40M | C40C | C20M | C20C | ExOs | O40M | O40C | O20M | O20C | |
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.00 | 3.86 | 2.76 | 2.13 | 0.97 | 2.28 | 3.28 | 3.17 | 2.33 | 2.38 |
| C2 | 3.17 | 2.96 | 1.55 | 2.53 | 2.21 | 2.95 | 0.88 | 0.00 | 1.36 | 1.58 |
| P | 1.00 | 2.00 | 2.00 | 1.00 | 1.00 | 1.00 | 2.00 | 2.00 | 2.00 | 2.00 |
Pasos 1 a 3#
for (paso in 1:3){
print(paste("Cálculo de los centros del paso",paso))
centroids(F,P)$centroids->C
print(round(C,2))
# "Distancias al cuadrado a los centros"
as.matrix(dist(rbind(F,C)))[11:12,1:10]->D;rownames(D)<-c("C1","C2")
cat("\n")
print(paste("Distancias al cuadrado y pertición",paso))
print(round(D,2))
cat("\n")
"Partición"
factor(D[1,]>D[2,],labels=c("I1","I2"))->P
print(P)
cat("\n")
cen<-cbind(cen,C)
#print(round(cen,2))
tab<-rbind(tab,rbind(D,P))
#print(round(tab,2))
# factor(D22>D21)->P
# tab<-rbind(tab,D21,D22,P)
# print(tab[paso+1:3,],digits=2)
}
[1] "Cálculo de los centros del paso 1"
Axis1 Axis2
I1 -0.67 -0.89
I2 0.44 0.60
[1] "Distancias al cuadrado y pertición 1"
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C
C1 0.82 3.41 2.12 1.81 0.24 2.00 2.51 2.35 1.58 1.68
C2 2.64 2.38 0.86 1.76 1.67 2.98 0.68 0.77 1.48 1.73
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C
I1 I2 I2 I2 I1 I1 I2 I2 I2 I1
Levels: I1 I2
[1] "Cálculo de los centros del paso 2"
Axis1 Axis2
I1 -1.27 -0.47
I2 0.85 0.31
[1] "Distancias al cuadrado y pertición 2"
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C
C1 1.27 3.96 2.53 2.47 0.90 1.27 2.69 2.28 1.14 1.14
C2 2.64 1.91 0.37 1.36 1.72 3.34 0.71 1.22 1.92 2.17
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C
I1 I2 I2 I2 I1 I1 I2 I2 I1 I1
Levels: I1 I2
[1] "Cálculo de los centros del paso 3"
Axis1 Axis2
I1 -1.23 -0.24
I2 1.23 0.25
[1] "Distancias al cuadrado y pertición 3"
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C
C1 1.47 3.91 2.44 2.49 0.97 1.26 2.54 2.08 0.91 0.92
C2 2.86 1.53 0.11 1.27 1.98 3.71 0.80 1.51 2.30 2.55
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C
I1 I2 I2 I2 I1 I1 I2 I2 I1 I1
Levels: I1 I2
Resumen#
round(cen,2)
round(tab,2)
| Axis1 | Axis2 | Axis1 | Axis2 | Axis1 | Axis2 | Axis1 | Axis2 | |
|---|---|---|---|---|---|---|---|---|
| C1 | -0.89 | -1.68 | -0.67 | -0.89 | -1.27 | -0.47 | -1.23 | -0.24 |
| C2 | 0.15 | 1.31 | 0.44 | 0.60 | 0.85 | 0.31 | 1.23 | 0.25 |
| ExCl | C40M | C40C | C20M | C20C | ExOs | O40M | O40C | O20M | O20C | |
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.00 | 3.86 | 2.76 | 2.13 | 0.97 | 2.28 | 3.28 | 3.17 | 2.33 | 2.38 |
| C2 | 3.17 | 2.96 | 1.55 | 2.53 | 2.21 | 2.95 | 0.88 | 0.00 | 1.36 | 1.58 |
| P | 1.00 | 2.00 | 2.00 | 1.00 | 1.00 | 1.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| C1 | 0.82 | 3.41 | 2.12 | 1.81 | 0.24 | 2.00 | 2.51 | 2.35 | 1.58 | 1.68 |
| C2 | 2.64 | 2.38 | 0.86 | 1.76 | 1.67 | 2.98 | 0.68 | 0.77 | 1.48 | 1.73 |
| P | 1.00 | 2.00 | 2.00 | 2.00 | 1.00 | 1.00 | 2.00 | 2.00 | 2.00 | 1.00 |
| C1 | 1.27 | 3.96 | 2.53 | 2.47 | 0.90 | 1.27 | 2.69 | 2.28 | 1.14 | 1.14 |
| C2 | 2.64 | 1.91 | 0.37 | 1.36 | 1.72 | 3.34 | 0.71 | 1.22 | 1.92 | 2.17 |
| P | 1.00 | 2.00 | 2.00 | 2.00 | 1.00 | 1.00 | 2.00 | 2.00 | 1.00 | 1.00 |
| C1 | 1.47 | 3.91 | 2.44 | 2.49 | 0.97 | 1.26 | 2.54 | 2.08 | 0.91 | 0.92 |
| C2 | 2.86 | 1.53 | 0.11 | 1.27 | 1.98 | 3.71 | 0.80 | 1.51 | 2.30 | 2.55 |
| P | 1.00 | 2.00 | 2.00 | 2.00 | 1.00 | 1.00 | 2.00 | 2.00 | 1.00 | 1.00 |
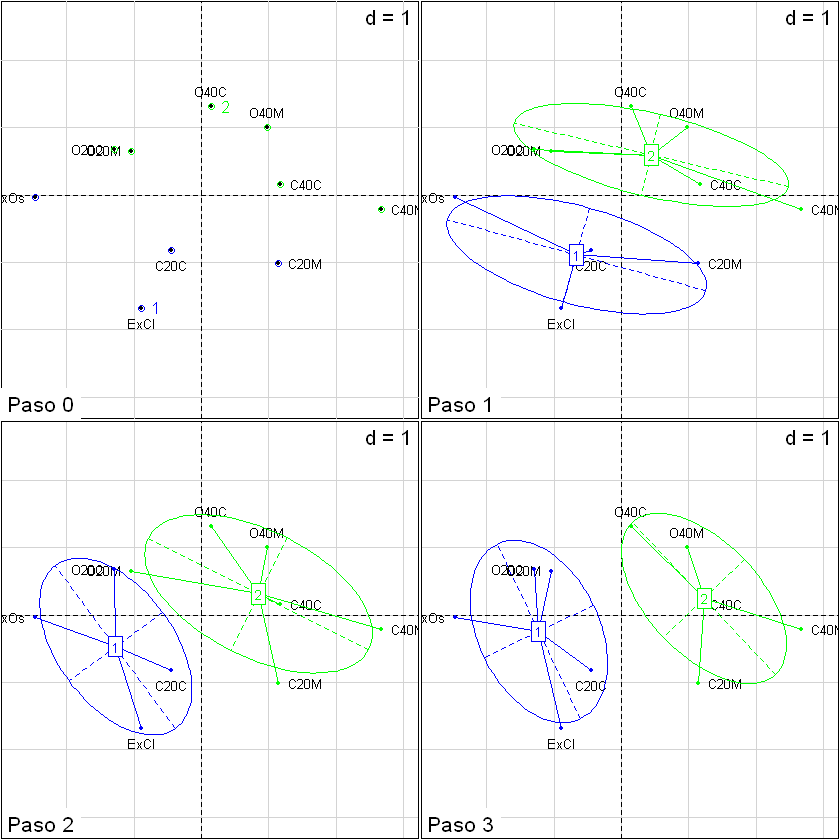
Proceso gráfico#
par(mfrow=c(2,2)) # 4 gráficas
plotfp(F,infaxes="no",main="Paso 0",cex=1.5)
text(x=cen[,1],y=cen[,2],labels=c("1","2"),col=c("blue","green"),pos=4)
points(F[tab[3,]==1,],col="blue")
points(F[tab[3,]==2,],col="green")
plotfp(F,infaxes="no",main="Paso 1",cex=1.5)
s.class(F,factor(tab[3,]),col=c("blue","green"),add.plot=TRUE)
plotfp(F,infaxes="no",main="Paso 2",cex=1.5)
s.class(F,factor(tab[6,]),col=c("blue","green"),add.plot=TRUE)
plotfp(F,infaxes="no",main="Paso 3",cex=1.5)
s.class(F,factor(tab[9,]),col=c("blue","green"),add.plot=TRUE)
Ventajas del K-means#
Es muy rápido
Poco exigente en recursos de cómputo
Desventajas del K-means#
Con un método de agrupamiento se pretende descubrir una estructura de clases en los grupos y el algoritmo \(K{-}means\) requiere que se le suministre el número de clases y los puntos iniciales.
En general, la inercia mínima que se obtiene depende de los puntos iniciales.
Métodos de clasificación jerárquica#
Aglomerativos: En Ciencias Naturales se denominan métodos de clasificación ascendente jerárquica aglomerativa
Divisivos
Nota
Estos métodos construyen una serie de particiones anidadas.
Clasificación jerárquica aglomerativa#
Algoritmo#
Calcular la matriz de distancias entre los \(n\) individuos,
Unir los dos más cercanos para tener una partición de \(n-1\) clases,
Calcular la distancia entre el nuevo grupo y los demás individuos,
Seleccionar los dos más cercanos, para conseguir una partición en \(n-2\) clases y
Continuar aglomerando hasta llegar a una partición de una clase con los \(n\) individuos.
El proceso de uniones se representa en un árbol de clasificación o dendrograma. % indexado por las distancias de las uniones.
Estos métodos requieren de un índice de similitud, disimilitud o distancia entre individuos.
En nuestro contexto se selecciona la distancia Euclidiana canónica.
Al conformar grupos se necesita definir una distancia entre ellos, que se denomina criterio de agregación y que le da nombre a un método específico. Por ejemplo:
enlace simple: distancia entre los dos individuos más cercanos cada uno de diferente grupo
enlace completo: distancia entre los dos individuos más lejanos.}
Distancia entre individuos#
Distancias para variables continuas#
Dos distancias para variables continuas#
Euclidiana#
Manhattan o Cityblock#
Distancias disponibles en la función dist{stats}#
Uso:
dist(x, method = "euclidean", diag = FALSE, upper = FALSE, p = 2)
Detalles:
Las medidas de distancia (escritas para dos vectores x e y) son: ‘euclidean’: Distancia usual entre dos vectores. $\(\sqrt(\sum((x_i - y_i)^2)).\)$
‘maximum’: Distancia máxima entre dos componentes de x e y (norma suprema) ‘manhattan’: Distancia absoluta entre dos vectores
‘canberra’:
Términos con cero, numerador y denominador son omitidos de la suma y tratados como valores faltantes
Distancias entre variables binarias disponibles en dist.binary{ade4}#
Tabla de contingencia \(2\times2\) contando coincidencias y no coincidencias de variables binarias entre dos individuos (n es el número de atributos):
Individuo l
| 1 | 0 | suma
--------------------
Individuos 1 | a | b | n_j
i 0 | c | d | c+d
--------------------
suma | n_k | b+d | n
Detalles:
Todas estas distancias son del tipo \(d = \sqrt{(1 - s)}\) con \(s\) un coeficiente de similaridad:
1 = Índice de Jaccard (1901) S3 coeficiente de Gower Legendre: \(s_1 = \dfrac{a}{a+b+c}\)
2 = Coeficiente simple de igualdad de Sokal & Michener (1958) S4 coeficiente de Gower & Legendre: \(s_2 = \dfrac{a+d}{a+b+c+d}\)
3 = Sokal & Sneath(1963) S5 coeficiente de Gower & Legendre: \(s_3 = \dfrac{a}{a + 2(b + c)}\)
4 = Rogers & Tanimoto (1960) S6 coeficiente de Gower & Legendre: \(s_4 = \dfrac{a + d}{a + 2(b + c) +d)}\)
5 = Dice (1945) or Sorensen (1948) S7 coeficiente de Gower & Legendre: \(s_5 =\dfrac{2a}{2a + b + c}\)
6 = Hamann coeficiente S9 índice de Gower & Legendre (1986): \(s_6 = \dfrac{- (b + c) + d}{a + b + c + d}\)
7 = Ochiai (1957) S12 coeficiente de Gower & Legendre: \(s-7 = \dfrac{a}{\sqrt{(a + b)(a + c)}}\)
8 = Sokal & Sneath (1963) S13 coeficiente de Gower & Legendre: \(s_8 =\dfrac{ad}{\sqrt{(a + b)(a + c)(d + b)(d + c)}}\)
9 = Phi de Pearson S14 coeficiente de Gower & Legendre: \(s_9 = \dfrac{ad -bc}{\sqrt{(a + b)(a + c)(d + b)(d + c)}}\)
10 = S2 coeficiente de Gower & Legendre: \(s_{10} =\dfrac{a}{a + b + c + d}\)
Distancias entre grupos = métodos de agregación#
Enlace simple#
La distancia entre dos grupos \(A\) y \(B\) es igual a la distancia de los dos individuos de diferente grupo más cercanos: $\( d(A,B) = \min \{ d(i,l); i \in A; l \in B \} \)$ Este criterio tiende a producir grupos alargados (efecto de encadenamiento), que pueden incluir elementos muy distintos en los extremos.
Enlace completo#
La distancia entre los dos grupos \(A\) y \(B\) es igual a la distancia entre los dos individuos de diferente grupo más alejados: $\( d(A,B) = \max \{ d(i,l); i \in A; l \in B \} \)$
El enlace completo tiende a producir grupos esféricos.
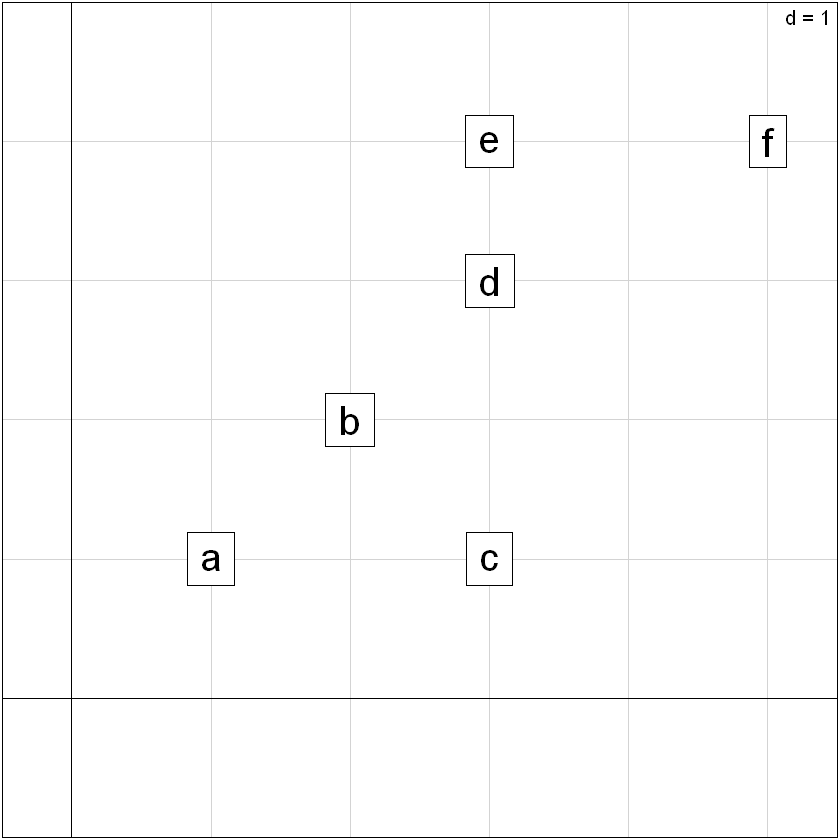
Ejemplo de «juguete» utilizando la distancia de Manhatan entre individuos y el enlace completo como distancia entre grupos.#
Sean los puntos a clasificar:
a<-c(1,1);b<-c(2,2);c<-c(3,1);d<-c(3,3);e<-c(3,4);f<-c(5,4)
X<-rbind(a,b,c,d,e,f)
s.label(X,clabel=2)
Las distancias de Manhattan son:
D<-dist(X,"manhattan");D
a b c d e
b 2
c 2 2
d 4 2 2
e 5 3 3 1
f 7 5 5 3 2
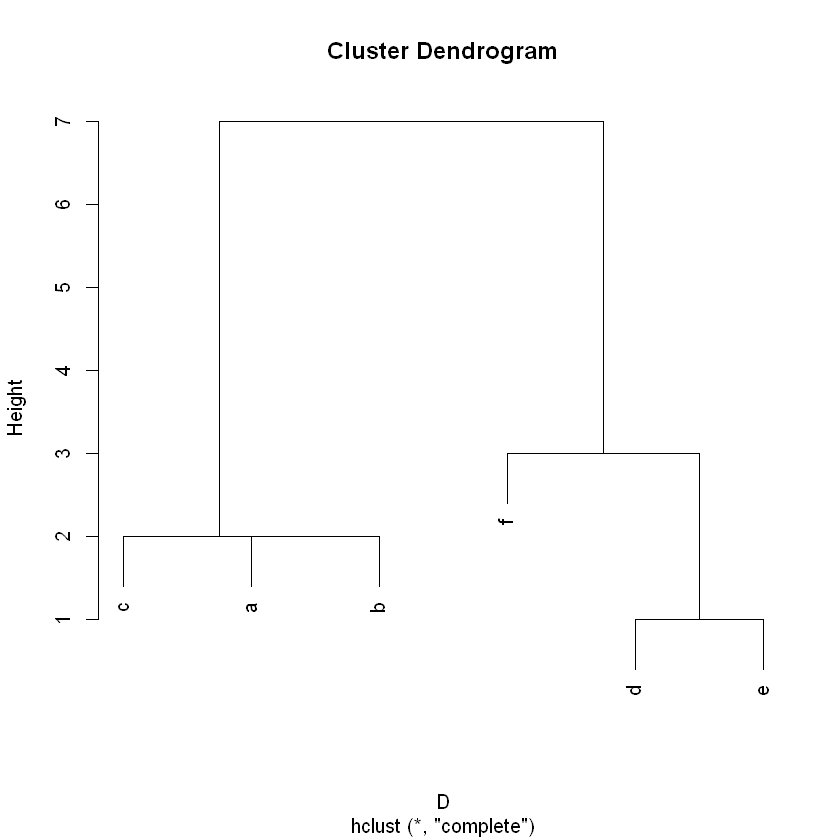
Pasos#
Se unen d y e a una distancia de 1
Se unen a y b a una distancia de 2
Se unen ab y c a una distancia de 2
Se unen de y f a una distancia de 3
Se unen abc y def a una distancia de 7
hc<-hclust(D)
data.frame(hc$merge,hc$height)
| X1 | X2 | hc.height |
|---|---|---|
| <int> | <int> | <dbl> |
| -4 | -5 | 1 |
| -1 | -2 | 2 |
| -3 | 2 | 2 |
| -6 | 1 | 3 |
| 3 | 4 | 7 |
Árbol o dendrograma#
plot(hc)
Ultramétrica asociada al árbol#
| a | b | c | d | e
-------------------
b | 2 |
c | 2 | 2
d | 7 | 7 | 7
e | 7 | 7 | 7 | 1
f | 7 | 7 | 7 | 3 | 3
Enlace promedio#
La distancia entre los dos grupos es el promedio de distancias entre todas las parejas de individuos de diferente grupo:
Método Ward#
Sean \(A\) y \(B\) clases no vacías y disyuntas y
Pesos: \(p_{_A}\), \(p_{_B}\) y
Centros de gravedad \(\mathbf{g}_{_A} \), \(\mathbf{g}_{_B}\),
Inercias intra grupo: \(I_{_A} \), \(I_{_B}\)
\(AB = A \bigcup B\): \(\mathbf{g}_{_{AB}}\) , \(I_{AB}\)
Inercia entre \(A\) y \(B\) = \(W(A,B)\)
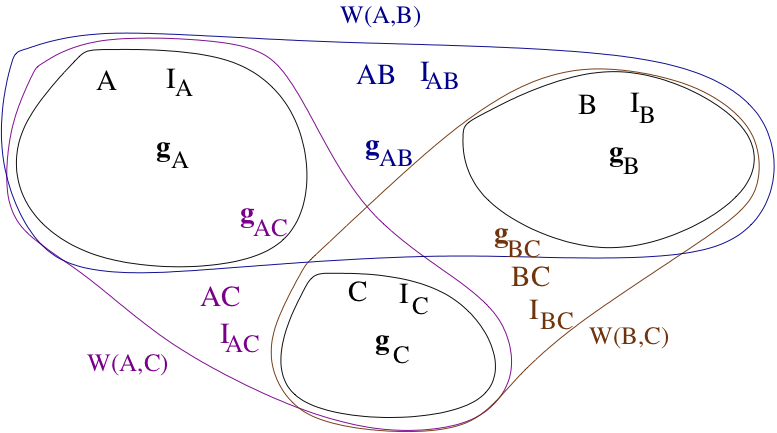
Distancia de Ward entre grupos $\( W(A,B) = \frac{p_{_A} p_{_B}}{p_{_A} + p_{_B}}d^{2}(\mathbf{g}_{_A} , \mathbf{g}_{_B}) \)$
Incremento de la inercia intra-grupos al unir los grupos \(A\) y \(B\) en uno solo.
Distancia de Ward entre dos individuos \(i\) y \(l\)
Distancia de Ward entre individuos $\( W(i,l) = \frac{p_i p_l}{p_i + p_l}d^{2}(i,l) \)$
pesos iguales a \(1/n\) para los dos individuos $\( W(i,l) = \frac{1}{2n}d^{2}(i,l) \)$
\(A\), \(B\) y \(C\) tres grupos presentes en el mismo paso de construcción del árbol.
se unen \(A\) y \(B\) para formar el grupo \(AB\)
Fórmula de recurrencia
Distancia de Ward $\( d(AB,C) = \frac{(p_{_A} + p_{_C})W(A,C)+(p_{_B} + p_{_C})W(B,C)-p_{_C} W(A,B)}{p_{_A} + p_{_B} + p_{_C}} \)$
Procedimiento para construir el árbol con el método de Ward#
Calcular la matriz de distancias de Ward entre parejas de individuos
Seleccionar la pareja de grupos (individuos en el primer paso) que presente la menor distancia de Ward para conformar el nuevo grupo.
Calcular las distancias entre todos los grupos y el grupo recién conformado utilizando la fórmula de distancia de Ward o la fórmula de recurrencia.
Eliminar las filas y columnas correspondientes a los individuos o grupos unidos y adicionar una fila y una columna para registrar las distancias entre el nuevo grupo y los demás.
Repetir el proceso hasta llegar a una sola clase.
De inercia entre clases a inercia intra-clases y viceversa#
Al formar el árbol#
Antes de empezar las uniones toda la inercia corresponde a inercia entre-clases (cada individuo es una clase)
A medida que llevan a cabo las uniones, la inercia entre-clases va pasando a inercia intra-clases
Al terminar, toda la inercia es intra-clases (todos los elementos conforman una clase)
La suma de los índices de nivel es igual a la inercia total
Al cortar el árbol sucesivamente#
En dos clases: el último índice de nivel es la inercia entre las dos clases.
En tres clases: la inercia entre clases es la suma de los dos últimos índices de nivel.
Hasta \(n\) clases de un individuo: toda la inercia es entre clases.
Ejemplo café#
Distancias de Ward entre cafés#
data(cafe)
Wcafe<-1/20*dist(F)^2;round(Wcafe,3)
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M
C40M 0.744
C40C 0.382 0.119
C20M 0.228 0.151 0.069
C20C 0.047 0.505 0.178 0.127
ExOs 0.259 1.328 0.668 0.700 0.236
O40M 0.537 0.220 0.039 0.207 0.268 0.650
O40C 0.501 0.437 0.120 0.320 0.244 0.434 0.039
O20M 0.273 0.730 0.259 0.377 0.126 0.126 0.211 0.093
O20C 0.284 0.828 0.319 0.438 0.147 0.095 0.263 0.124 0.003
Construcción del árbol#
hclCafe<-ward.cluster(dista=dist(F),h.clust=1) # función de FactoClass
plot(hclCafe)
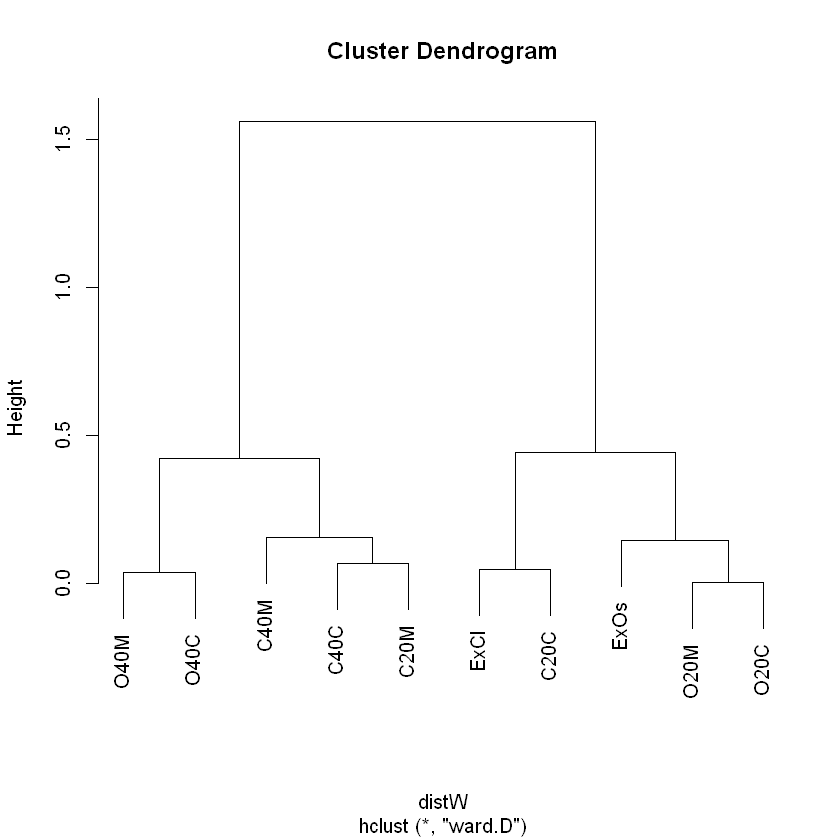
W<-1/20*dist(F)^2;round(W,3)
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M
C40M 0.744
C40C 0.382 0.119
C20M 0.228 0.151 0.069
C20C 0.047 0.505 0.178 0.127
ExOs 0.259 1.328 0.668 0.700 0.236
O40M 0.537 0.220 0.039 0.207 0.268 0.650
O40C 0.501 0.437 0.120 0.320 0.244 0.434 0.039
O20M 0.273 0.730 0.259 0.377 0.126 0.126 0.211 0.093
O20C 0.284 0.828 0.319 0.438 0.147 0.095 0.263 0.124 0.003
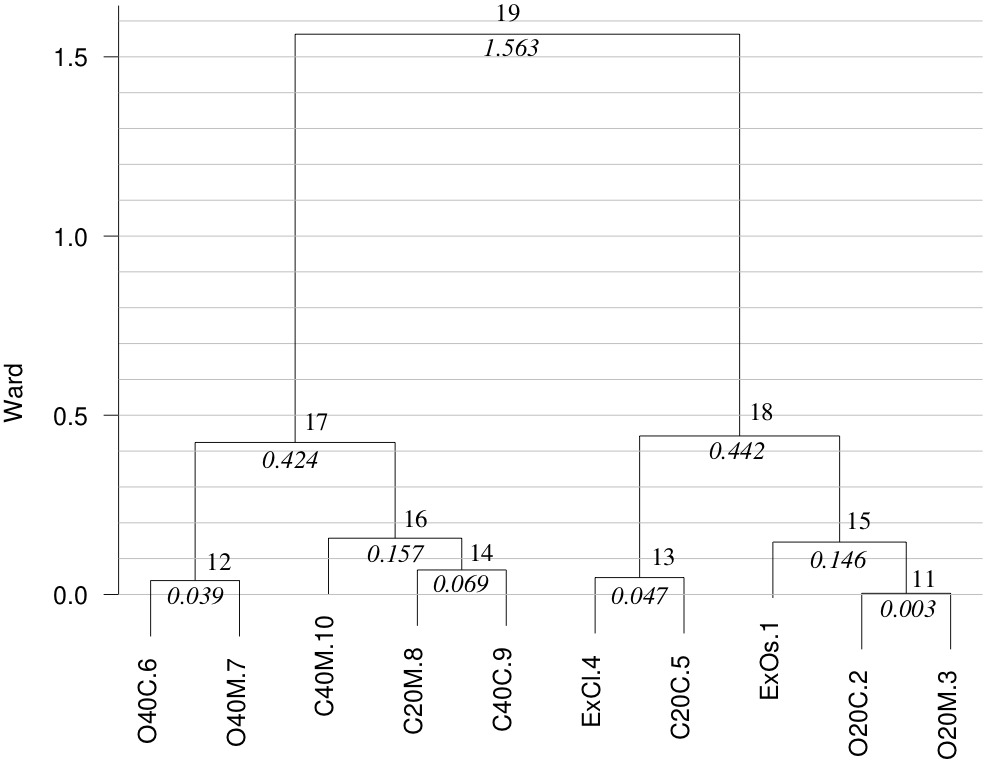
hclCafe<-ward.cluster(dista=dist(F),h.clust=2)
Nodo=hclCafe$Nodo;Ward=round(hclCafe$Indice,3);SumaWard=round(cumsum(hclCafe$Indice),3)
t(data.frame(Nodo,Ward,SumaWard))
| Nodo | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|
| Ward | 0.003 | 0.039 | 0.047 | 0.069 | 0.146 | 0.157 | 0.424 | 0.442 | 1.563 |
| SumaWard | 0.003 | 0.042 | 0.089 | 0.158 | 0.304 | 0.461 | 0.885 | 1.327 | 2.890 |
Combinación de métodos#
Desde el punto de vista del análisis de datos los métodos a utilizar son: el de Ward de aglomeración jerárquica y el K-means, porque buscan grupos que tengan inercia intragrupos lo más baja posible. Estos métodos se complementan para subsanar entre sí las desventajas y aprovechar sus ventajas.
Los métodos de clasificación jerárquica tienen dos desventajas: utilizan mayor recurso de cómputo y las particiones obtenidas quedan anidadas.
El K-means tiene también dos problemas: hay que darle el número de clases iniciales y los puntos iniciales. El número de clases es precisamente lo que se quiere descubrir en una tabla de datos y el óptimo es local, es decir, depende de los puntos iniciales.
La estrategia programada en DtmVic y FactoClass, combina los dos métodos, ya que sus ventajas y desventajas son complementarias. Cuando el número de elementos a clasificar no es tan grande y el equipo de cálculo lo permite, se realiza la clasificación jerárquica aglomerativa con el método de Ward. El «histograma de índices de nivel» permite visualizar las mejores alturas de corte del árbol, y por ende, el número de clases. Luego, se disminuye la inercia intraclases de la partición obtenida utilizando K-means, con los centros de gravedad de la partición derivada de cortar el árbol como puntos iniciales.
Clasificación a partir de coordenadas#
Los métodos factoriales se pueden utilizar para transformar los datos antes de realizar procedimientos de clasificación automática. Una de las salidas de un análisis factorial es una tabla de individuos por coordenadas factoriales.
Entonces, las columnas de las tablas de entrada de los métodos de clasificación son de la misma naturaleza: coordenadas factoriales, que son de variables continuas.
En ese sentido, los métodos factoriales pueden cumplir con dos funciones: la primera, en el caso de análisis de correspondencias, es la transformación de unas variables cualitativas en otras continuas; la segunda es una función de filtro, al considerar que los \(S\) primeros ejes factoriales contienen la información y los otros son ruido.
En otras palabras, ACP y los AC, son métodos de pretratamiento de datos para la clasificación que pueden cumplir con dos funciones: cuantificar las variables cualitativas y reducir la dimensionalidad de los datos.
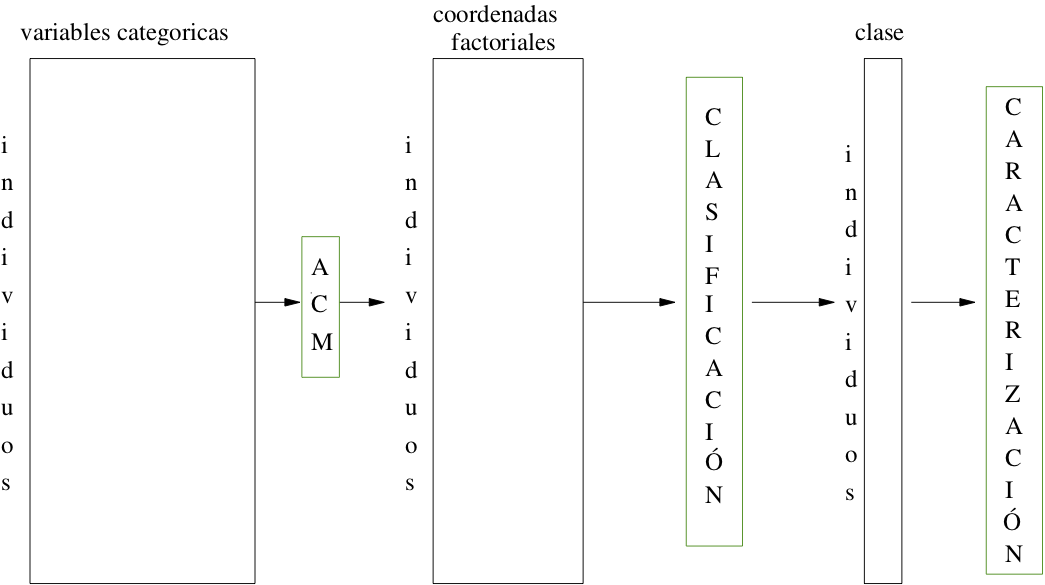
Función de transformación o cuantificación#
Un programa de ACP normado recibe los datos originales y los estandariza antes de obtener valores y vectores propios, y coordenadas factoriales de individuos y variables.
En un análisis de correspondencias las coordenadas factoriales se constituyen en nuevas variables continuas, con las que se puede utilizar la combinación de métodos de clasificación para variables continuas.
Función de filtro#
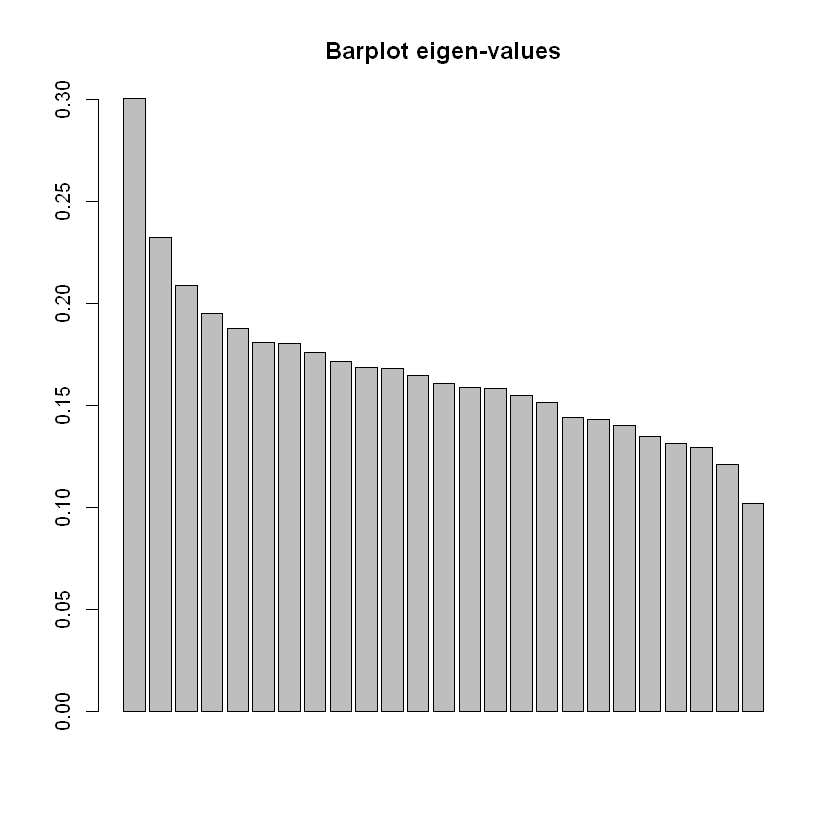
Conectar un método factorial con la clasificación da la posibilidad de seleccionar el número de ejes a utilizar en esta clasificación. Se utiliza el histograma de valores propios y otros criterios para la selección del número de ejes, pero haciendo énfasis en el sentido de filtro: aquí seleccionar más ejes puede significar mayor recurso de cómputo, pero no más trabajo para el analista.
En problemas pequeños y medianos el recurso de cómputo no tiene importancia. En general, el número de ejes para la clasificación es mayor que el número de ejes seleccionados para analizar en un método factorial.
Muchas veces se utilizan todos los ejes para la clasificación, lo que es equivalente a realizar el análisis con las variables originales.
Caracterización automática de las clases#
En términos generales, en un procedimiento de clasificación se obtiene una variable cualitativa indicadora de la clase o grupo al que pertenece cada elemento clasificado. Esta variable se puede cruzar con cualquiera de las variables presentes en la tabla de datos correspondiente.
Los procedimientos para describir dos variables se pueden utilizar para ese propósito, en particular los ordenamientos por valores test.
Las variables continuas o las categorías de las variables cualitativas con diferencias que generan un valor test superior a un umbral, generalmente 2, se dice que caracterizan a la clase.
Las que generan valores test inferiores al umbral son de signo negativo (-2, por ejemplo) y se dice que caracterizan negativamente a la clase respectiva.
Descripción con variables continuas#
La clase es la variable cualitativa que se desea describir con las variables continuas.
Las variables continuas que caracterizan a una clase son aquellas que tienen la media de la clase suficientemente diferente de la media global.
Para encontrarlas y ordenarlas se hace la comparación de la media dentro de la clase con la media global, siguiendo el procedimiento de ordenamiento mediante valores test.
Donde \(\mu\) y \(\sigma^2\) son la media y varianza globlales (de todos los datos); \(n_k\) y \(\bar{x} _k\) el número y la media del grupo de individuos que asumen la categoría \(k\) .
En la presentación de los resultados se pueden incluir los boxplots de las variables que caracterizan a una o más clases.
Descripción con variables cualitativas#
Una categoría es característica de una clase si su frecuencia dentro de la clase es suficientemente diferente de su frecuencia global.
Para encontrarlas y ordenarlas se utiliza el procedimiento de valores test (ver capítulo 7 del libro EDM)
Para las variables que tengan categorías que caracterizan a las clases se pueden obtener las gráficas de perfiles de las clases
Una estrategia de clasificación#
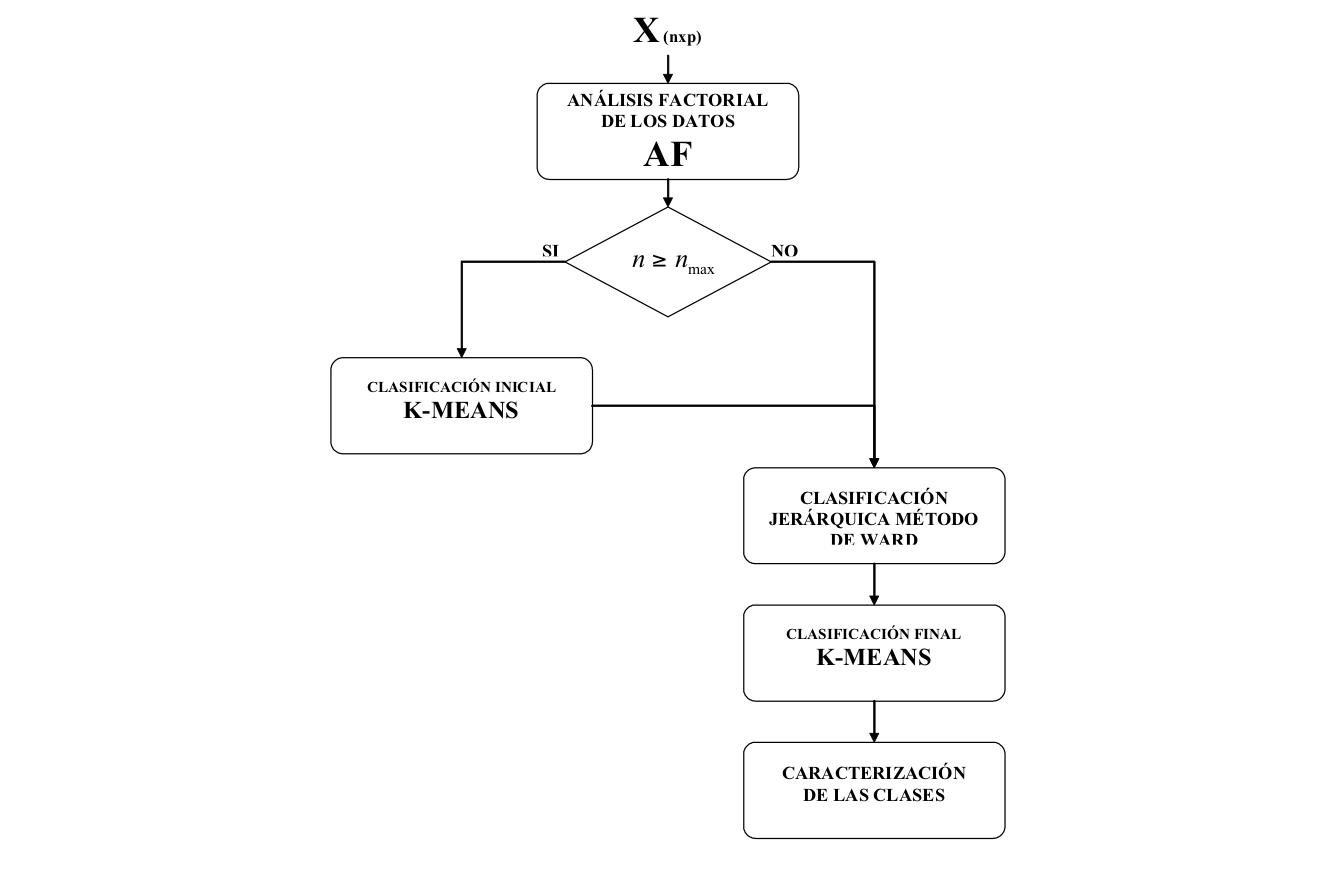
La estrategia de clasificación que se ha propuesto, se resume en los siguientes pasos:
Realizar el análisis en ejes principales correspondiente.
Seleccionar el número de ejes para la clasificación.
Si el número de «individuos» es muy grande, realizar un K-means de preagrupamiento en miles de clases.
Realizar la clasificación jerárquica con el método de Ward sobre los «individuos» o los grupos del paso anterior.
Decidir el número de clases y cortar el árbol.
Realizar K-means de consolidación partiendo de los centros de gravedad de la partición obtenida al cortar el árbol.
Caracterizar las clases.
Proyección de las clases sobre los planos factoriales.
Ejemplo de aplicación: Clasificación de los niños según el consumo cultural#
Objetivo
Complementar la descripción del consumo cultural realizada con análisis de correspondencias múltiples.
La función FactoClass{FactoClass}
load(url("https://github.com/AprendizajeProfundo/Libro-Fundamentos/blob/main/Machine_Learning/Datos/ninios8a11.Rda?raw=true"))
#load("../Datos/ninios8a11.Rda")
ninios8a11$Edad<-factor(ninios8a11$Edad)
# variables activas
Y <- subset(ninios8a11,select=c(Teat,Libr,Cine,Vide,Radi,Musi))
# variables suplementarias
Ys<-ninios8a11[,c(2,29,30,32,35)]
Variables activas#
par(las=1,mfrow=c(2,3),mai=c(0.55,0.5,0.1,0.1))
for(i in 1:6){
cat<-attributes(Y[,i])$levels;
per<-tabulate(Y[,i])/nrow(Y)*100;
pl<-plot(Y[,i],horiz=TRUE,col=gray(seq(1.0,0.9,
length=length(cat))),ylim=c(0,8),
xlim=c(0,1400),xlab=colnames(Y)[i]);
text(800,pl,round(per,1),cex=0.8,pos=4);
}

Variables ilustrativas#
par(las=1,mfrow=c(2,3),mai=c(0.55,0.5,0,0.1))
for(i in 1:5){
cat<-attributes(Y[,i])$levels;
per<-tabulate(Ys[,i])/nrow(Y)*100;
pl<-plot(Ys[,i],horiz=TRUE,col=gray(seq(1.0,0.9,
length=length(cat))),ylim=c(0,8),
xlim=c(0,1000),xlab=colnames(Ys)[i]);
text(100,pl,round(per,1),cex=0.8,pos=4);
}
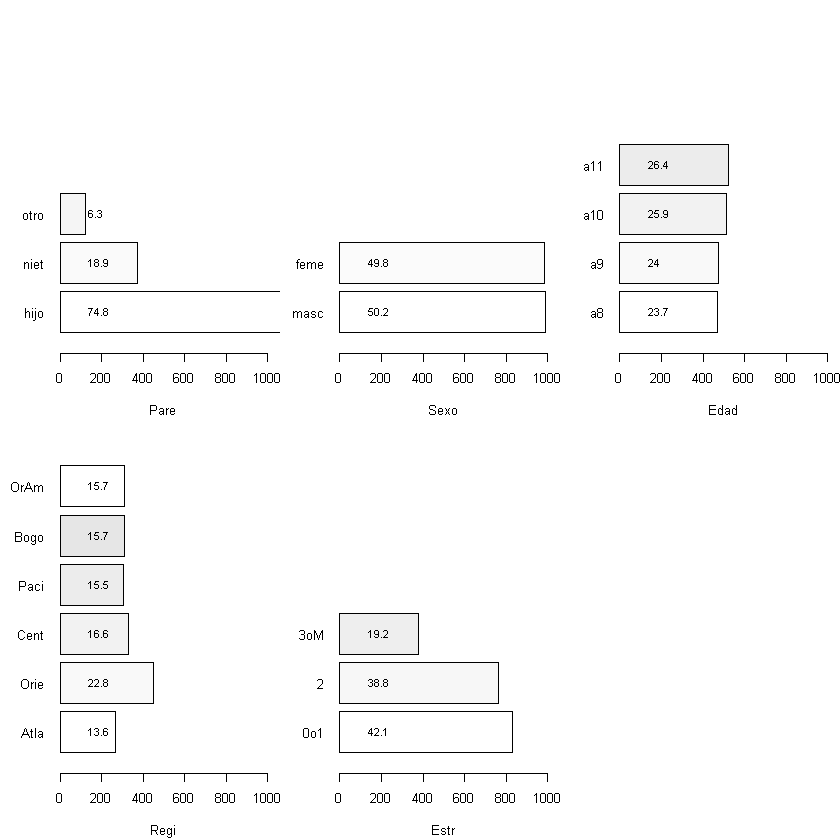
install.packages('Factoclass')
library(FactoClass)
Installing package into 'C:/Users/User/AppData/Local/R/win-library/4.2'
(as 'lib' is unspecified)
Warning message:
"package 'Factoclass' is not available for this version of R
A version of this package for your version of R might be available elsewhere,
see the ideas at
https://cran.r-project.org/doc/manuals/r-patched/R-admin.html#Installing-packages"
Warning message:
"Perhaps you meant 'FactoClass' ?"
fcConCul <- FactoClass(dfact=Y,metodo=dudi.acm,dfilu=Ys , nf = 3, nfcl = 5, k.clust = 4,
scanFC = FALSE)
The number of retained axes for factorial analysis is 3
The number of axes for clustering is 5
Look the histogram of 25 indexes
Partition in 4 clusters
names(fcConCul)
- 'dudi2'
- 'dudi'
- 'nfcl'
- 'k'
- 'indices'
- 'cluster'
- 'cor.clus'
- 'clus.summ'
- 'carac.cont'
- 'carac.cate'
- 'carac.frec'
barplot(fcConCul$dudi$eig,main="Barplot eigen-values")
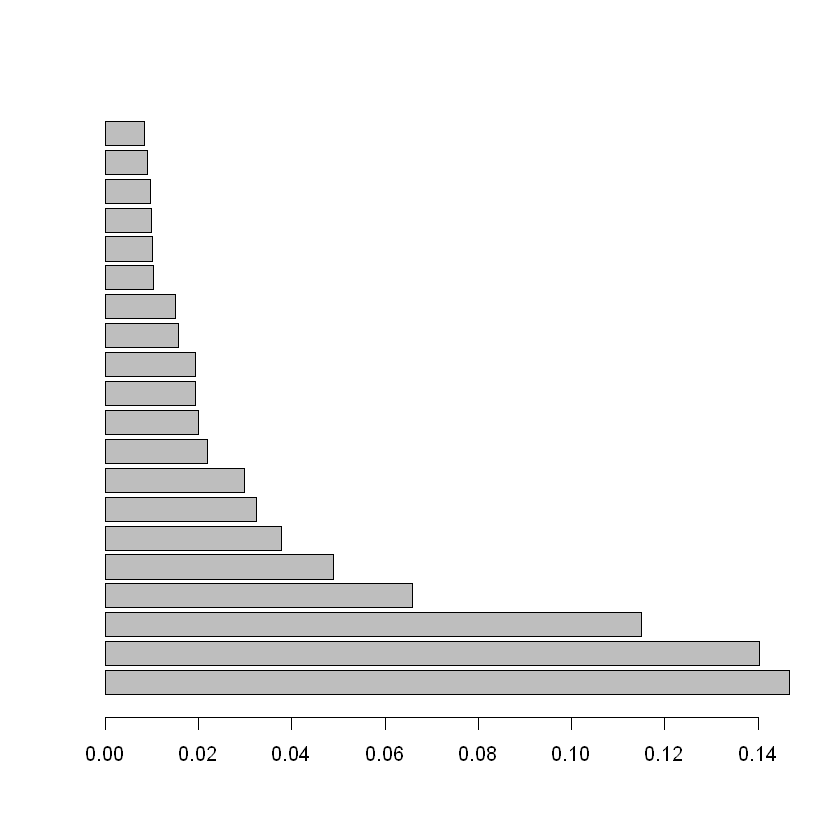
ultimosNodos<-tail(fcConCul$indices,20)
ultimosNodos
barplot(ultimosNodos$Indice[20:1],horiz=TRUE)
| Nodo | Prim | Benj | Indice | |
|---|---|---|---|---|
| <fct> | <fct> | <fct> | <dbl> | |
| 1951 | 3922 | 3872 | 3880 | 0.008481887 |
| 1952 | 3923 | 3871 | 3916 | 0.009042694 |
| 1953 | 3924 | 3886 | 3907 | 0.009735317 |
| 1954 | 3925 | 3883 | 3891 | 0.009909993 |
| 1955 | 3926 | 3896 | 3909 | 0.010150002 |
| 1956 | 3927 | 3908 | 3924 | 0.010420663 |
| 1957 | 3928 | 3912 | 3925 | 0.015028345 |
| 1958 | 3929 | 3918 | 3922 | 0.015680180 |
| 1959 | 3930 | 3913 | 3921 | 0.019286347 |
| 1960 | 3931 | 3919 | 3927 | 0.019344170 |
| 1961 | 3932 | 3905 | 3917 | 0.019969486 |
| 1962 | 3933 | 3923 | 3932 | 0.021916391 |
| 1963 | 3934 | 3911 | 3928 | 0.029784351 |
| 1964 | 3935 | 3915 | 3929 | 0.032529945 |
| 1965 | 3936 | 3930 | 3934 | 0.037830403 |
| 1966 | 3937 | 3920 | 3931 | 0.049002642 |
| 1967 | 3938 | 3926 | 3933 | 0.065875449 |
| 1968 | 3939 | 3935 | 3938 | 0.114914438 |
| 1969 | 3940 | 3937 | 3939 | 0.140346874 |
| 1970 | 3941 | 3936 | 3940 | 0.146772084 |
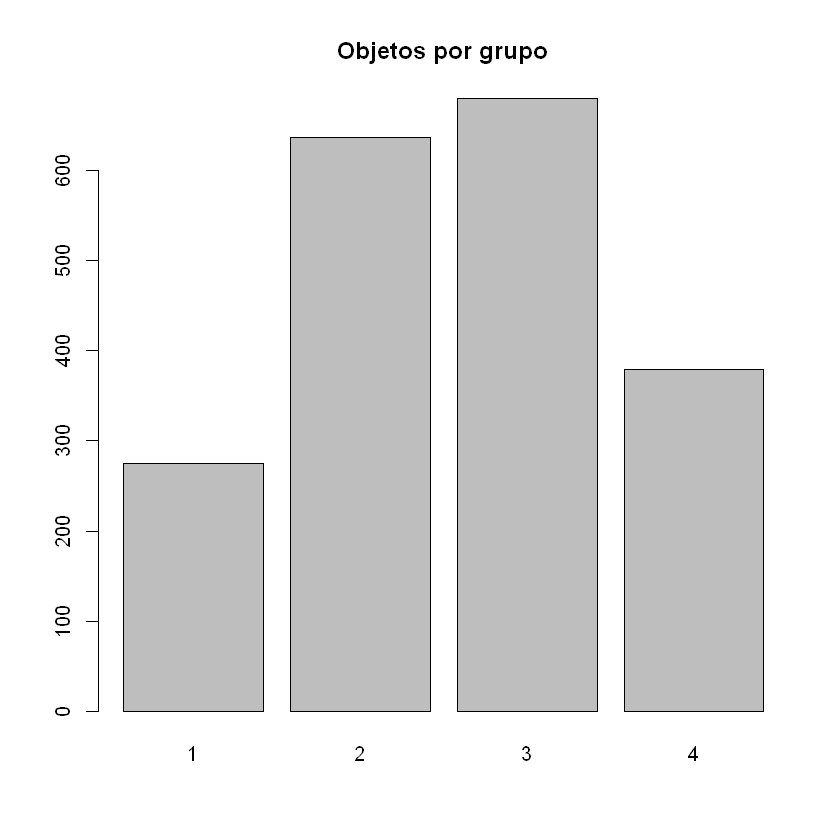
summary(fcConCul$cluster)
barplot(summary(fcConCul$cluster),main="Objetos por grupo")
- 1
- 275
- 2
- 637
- 3
- 680
- 4
- 379
fcConCul$clus.summ
| Bef.Size | Aft.Size | Bef.Inertia | Aft.Inertia | Bef.Weight | Aft.Weight | Bef.Dist_2 | Aft.Dist_2 | |
|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 310 | 275 | 0.1812 | 0.1520 | 0.1573 | 0.1395 | 0.7341 | 0.8417 |
| 2 | 592 | 637 | 0.2117 | 0.2064 | 0.3004 | 0.3232 | 0.2625 | 0.2976 |
| 3 | 530 | 680 | 0.1105 | 0.1407 | 0.2689 | 0.3450 | 0.3780 | 0.3626 |
| 4 | 539 | 379 | 0.2196 | 0.1544 | 0.2735 | 0.1923 | 0.4090 | 0.7021 |
| TOTAL | 1971 | 1971 | 0.7230 | 0.6535 | 1.0001 | 1.0000 | NA | NA |
fcConCul$carac.cate
class: 1
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.sema 23.962 0.000 92.9 52.7 7.9 156
Vide.mens 15.698 0.000 81.6 29.1 5.0 98
Radi.sema 15.600 0.000 80.8 29.1 5.0 99
Teat.trim 4.752 0.000 29.2 13.8 6.6 130
Vide.sema 4.503 0.000 21.0 30.9 20.5 404
Libr.sema 4.283 0.000 22.0 24.4 15.4 304
Teat.sema 2.858 0.004 27.6 5.8 2.9 58
Cine.anua 2.444 0.015 20.1 12.0 8.3 164
Regi.Cent 2.437 0.015 18.0 21.5 16.6 328
Regi.Atla 2.330 0.020 18.3 17.8 13.6 268
Teat.anua 2.312 0.021 19.8 11.6 8.2 162
Cine.trim 2.264 0.024 18.8 14.2 10.5 207
Libr.mens 2.193 0.028 20.2 9.5 6.5 129
Libr.anua 2.112 0.035 23.6 4.7 2.8 55
Regi.Bogo 2.097 0.036 17.4 19.6 15.7 310
Cine.mens -2.603 0.009 8.0 5.1 8.8 174
Radi.vdse -3.657 0.000 8.6 12.4 20.0 394
Libr.no -3.767 0.000 9.1 15.6 24.1 475
Regi.Orie -3.929 0.000 8.7 14.2 22.8 450
Vide.diar -4.199 0.000 5.7 4.7 11.5 227
Vide.vdse -4.338 0.000 9.7 25.1 36.3 715
Musi.vdse -5.105 0.000 8.8 22.5 35.7 703
Teat.no -5.485 0.000 11.3 58.5 72.6 1430
Musi.diar -5.568 0.000 5.0 5.8 16.2 319
Radi.no -6.560 0.000 9.4 37.1 55.3 1089
Vide.no -7.253 0.000 5.3 10.2 26.7 527
Musi.no -8.124 0.000 6.6 18.9 40.2 793
------------------------------------------------------------
class: 2
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.vdse 27.667 0.000 71.1 78.5 35.7 703
Vide.vdse 18.830 0.000 58.7 65.9 36.3 715
Radi.vdse 13.752 0.000 62.2 38.5 20.0 394
Libr.vdse 9.652 0.000 47.8 45.2 30.5 602
Libr.anua 4.034 0.000 58.2 5.0 2.8 55
Cine.seme 3.886 0.000 46.9 10.7 7.4 145
Teat.seme 3.296 0.001 46.7 7.8 5.4 107
Libr.sema 2.533 0.011 38.2 18.2 15.4 304
Estr.3oM 2.375 0.018 37.0 22.0 19.2 378
Libr.mens 2.347 0.019 41.1 8.3 6.5 129
Cine.mens 2.331 0.020 39.7 10.8 8.8 174
Regi.Cent -2.178 0.029 27.7 14.3 16.6 328
Teat.mens -2.382 0.017 21.4 2.8 4.3 84
Cine.no -2.891 0.004 30.2 60.8 65.0 1281
Estr.0o1 -2.998 0.003 28.8 37.5 42.1 829
Radi.no -3.429 0.001 29.2 49.9 55.3 1089
Radi.sema -6.762 0.000 5.1 0.8 5.0 99
Radi.diar -7.179 0.000 17.7 10.8 19.7 389
Libr.diar -7.807 0.000 14.8 7.5 16.4 324
Vide.diar -7.907 0.000 11.0 3.9 11.5 227
Vide.mens -8.610 0.000 0.0 0.0 5.0 98
Libr.no -8.769 0.000 16.6 12.4 24.1 475
Musi.diar -9.768 0.000 10.7 5.3 16.2 319
Musi.sema -10.675 0.000 0.6 0.2 7.9 156
Vide.no -14.079 0.000 9.5 7.8 26.7 527
Musi.no -15.757 0.000 12.9 16.0 40.2 793
------------------------------------------------------------
class: 3
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.no 28.646 0.000 71.0 82.8 40.2 793
Vide.no 25.055 0.000 79.1 61.3 26.7 527
Radi.no 14.640 0.000 48.3 77.4 55.3 1089
Libr.no 14.359 0.000 62.3 43.5 24.1 475
Teat.no 13.949 0.000 43.1 90.7 72.6 1430
Cine.no 12.218 0.000 43.8 82.5 65.0 1281
Estr.0o1 8.366 0.000 45.0 54.9 42.1 829
Regi.Orie 5.393 0.000 45.1 29.9 22.8 450
Regi.OrAm 3.766 0.000 43.7 19.9 15.7 309
Libr.trim 3.052 0.002 50.0 6.0 4.2 82
Edad.a10 -2.085 0.037 31.2 23.4 25.9 510
Teat.sema -2.715 0.007 19.0 1.6 2.9 58
Vide.sema -2.934 0.003 28.7 17.1 20.5 404
Cine.anua -3.207 0.001 23.8 5.7 8.3 164
Teat.mens -3.498 0.000 17.9 2.2 4.3 84
Estr.2 -3.611 0.000 29.8 33.5 38.8 764
Libr.anua -3.714 0.000 12.7 1.0 2.8 55
Cine.seme -4.035 0.000 20.0 4.3 7.4 145
Regi.Atla -4.690 0.000 22.4 8.8 13.6 268
Libr.mens -4.793 0.000 16.3 3.1 6.5 129
Regi.Bogo -5.146 0.000 22.3 10.1 15.7 310
Libr.vdse -5.151 0.000 26.4 23.4 30.5 602
Vide.mens -5.398 0.000 11.2 1.6 5.0 98
Cine.trim -5.952 0.000 16.9 5.1 10.5 207
Estr.3oM -6.429 0.000 20.9 11.6 19.2 378
Libr.diar -6.515 0.000 19.4 9.3 16.4 324
Radi.sema -6.563 0.000 7.1 1.0 5.0 99
Teat.seme -6.717 0.000 7.5 1.2 5.4 107
Teat.trim -6.884 0.000 9.2 1.8 6.6 130
Teat.anua -7.305 0.000 10.5 2.5 8.2 162
Radi.diar -7.472 0.000 19.0 10.9 19.7 389
Radi.vdse -7.780 0.000 18.5 10.7 20.0 394
Cine.mens -8.067 0.000 9.2 2.4 8.8 174
Vide.diar -9.123 0.000 9.7 3.2 11.5 227
Musi.sema -9.632 0.000 3.8 0.9 7.9 156
Musi.diar -11.212 0.000 9.4 4.4 16.2 319
Vide.vdse -13.541 0.000 15.9 16.8 36.3 715
Musi.vdse -16.819 0.000 11.5 11.9 35.7 703
------------------------------------------------------------
class: 4
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.diar 24.691 0.000 74.9 63.1 16.2 319
Vide.diar 19.378 0.000 73.6 44.1 11.5 227
Libr.diar 14.956 0.000 52.2 44.6 16.4 324
Radi.diar 14.870 0.000 48.1 49.3 19.7 389
Cine.mens 7.637 0.000 43.1 19.8 8.8 174
Teat.mens 6.972 0.000 52.4 11.6 4.3 84
Cine.trim 5.984 0.000 35.7 19.5 10.5 207
Teat.anua 5.779 0.000 37.7 16.1 8.2 162
Estr.3oM 4.350 0.000 27.2 27.2 19.2 378
Regi.Atla 2.827 0.005 25.4 17.9 13.6 268
Regi.Bogo 2.546 0.011 24.2 19.8 15.7 310
Teat.seme 2.015 0.044 26.2 7.4 5.4 107
Estr.2 2.015 0.044 21.2 42.7 38.8 764
Regi.Orie -2.473 0.013 15.6 18.5 22.8 450
Vide.sema -2.582 0.010 15.1 16.1 20.5 404
Libr.anua -2.943 0.003 5.5 0.8 2.8 55
Vide.vdse -3.206 0.001 15.7 29.6 36.3 715
Vide.mens -3.456 0.001 7.1 1.8 5.0 98
Radi.sema -3.497 0.000 7.1 1.8 5.0 99
Regi.OrAm -4.108 0.000 11.3 9.2 15.7 309
Libr.vdse -4.378 0.000 13.6 21.6 30.5 602
Libr.no -4.837 0.000 12.0 15.0 24.1 475
Radi.vdse -5.136 0.000 10.7 11.1 20.0 394
Libr.sema -5.202 0.000 9.2 7.4 15.4 304
Estr.0o1 -5.398 0.000 13.8 30.1 42.1 829
Musi.sema -6.483 0.000 2.6 1.1 7.9 156
Radi.no -7.657 0.000 13.1 37.7 55.3 1089
Teat.no -8.901 0.000 14.2 53.6 72.6 1430
Musi.no -9.257 0.000 9.6 20.1 40.2 793
Musi.vdse -9.444 0.000 8.5 15.8 35.7 703
Cine.no -9.445 0.000 13.0 43.8 65.0 1281
Vide.no -9.771 0.000 6.1 8.4 26.7 527
cluster.carac(Y,fcConCul$cluster,tipo.v="no",v.lim= 5,dn=3,dm=3,neg=TRUE)
class: 1
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.sema 23.962 0 92.9 52.7 7.9 156
Vide.mens 15.698 0 81.6 29.1 5.0 98
Radi.sema 15.600 0 80.8 29.1 5.0 99
Musi.vdse -5.105 0 8.8 22.5 35.7 703
Teat.no -5.485 0 11.3 58.5 72.6 1430
Musi.diar -5.568 0 5.0 5.8 16.2 319
Radi.no -6.560 0 9.4 37.1 55.3 1089
Vide.no -7.253 0 5.3 10.2 26.7 527
Musi.no -8.124 0 6.6 18.9 40.2 793
------------------------------------------------------------
class: 2
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.vdse 27.667 0 71.1 78.5 35.7 703
Vide.vdse 18.830 0 58.7 65.9 36.3 715
Radi.vdse 13.752 0 62.2 38.5 20.0 394
Libr.vdse 9.652 0 47.8 45.2 30.5 602
Radi.sema -6.762 0 5.1 0.8 5.0 99
Radi.diar -7.179 0 17.7 10.8 19.7 389
Libr.diar -7.807 0 14.8 7.5 16.4 324
Vide.diar -7.907 0 11.0 3.9 11.5 227
Vide.mens -8.610 0 0.0 0.0 5.0 98
Libr.no -8.769 0 16.6 12.4 24.1 475
Musi.diar -9.768 0 10.7 5.3 16.2 319
Musi.sema -10.675 0 0.6 0.2 7.9 156
Vide.no -14.079 0 9.5 7.8 26.7 527
Musi.no -15.757 0 12.9 16.0 40.2 793
------------------------------------------------------------
class: 3
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.no 28.646 0 71.0 82.8 40.2 793
Vide.no 25.055 0 79.1 61.3 26.7 527
Radi.no 14.640 0 48.3 77.4 55.3 1089
Libr.no 14.359 0 62.3 43.5 24.1 475
Teat.no 13.949 0 43.1 90.7 72.6 1430
Cine.no 12.218 0 43.8 82.5 65.0 1281
Libr.vdse -5.151 0 26.4 23.4 30.5 602
Vide.mens -5.398 0 11.2 1.6 5.0 98
Cine.trim -5.952 0 16.9 5.1 10.5 207
Libr.diar -6.515 0 19.4 9.3 16.4 324
Radi.sema -6.563 0 7.1 1.0 5.0 99
Teat.seme -6.717 0 7.5 1.2 5.4 107
Teat.trim -6.884 0 9.2 1.8 6.6 130
Teat.anua -7.305 0 10.5 2.5 8.2 162
Radi.diar -7.472 0 19.0 10.9 19.7 389
Radi.vdse -7.780 0 18.5 10.7 20.0 394
Cine.mens -8.067 0 9.2 2.4 8.8 174
Vide.diar -9.123 0 9.7 3.2 11.5 227
Musi.sema -9.632 0 3.8 0.9 7.9 156
Musi.diar -11.212 0 9.4 4.4 16.2 319
Vide.vdse -13.541 0 15.9 16.8 36.3 715
Musi.vdse -16.819 0 11.5 11.9 35.7 703
------------------------------------------------------------
class: 4
Test.Value p.Value Class.Cat Cat.Class Global Weight
Musi.diar 24.691 0 74.9 63.1 16.2 319
Vide.diar 19.378 0 73.6 44.1 11.5 227
Libr.diar 14.956 0 52.2 44.6 16.4 324
Radi.diar 14.870 0 48.1 49.3 19.7 389
Cine.mens 7.637 0 43.1 19.8 8.8 174
Teat.mens 6.972 0 52.4 11.6 4.3 84
Cine.trim 5.984 0 35.7 19.5 10.5 207
Teat.anua 5.779 0 37.7 16.1 8.2 162
Radi.vdse -5.136 0 10.7 11.1 20.0 394
Libr.sema -5.202 0 9.2 7.4 15.4 304
Musi.sema -6.483 0 2.6 1.1 7.9 156
Radi.no -7.657 0 13.1 37.7 55.3 1089
Teat.no -8.901 0 14.2 53.6 72.6 1430
Musi.no -9.257 0 9.6 20.1 40.2 793
Musi.vdse -9.444 0 8.5 15.8 35.7 703
Cine.no -9.445 0 13.0 43.8 65.0 1281
Vide.no -9.771 0 6.1 8.4 26.7 527
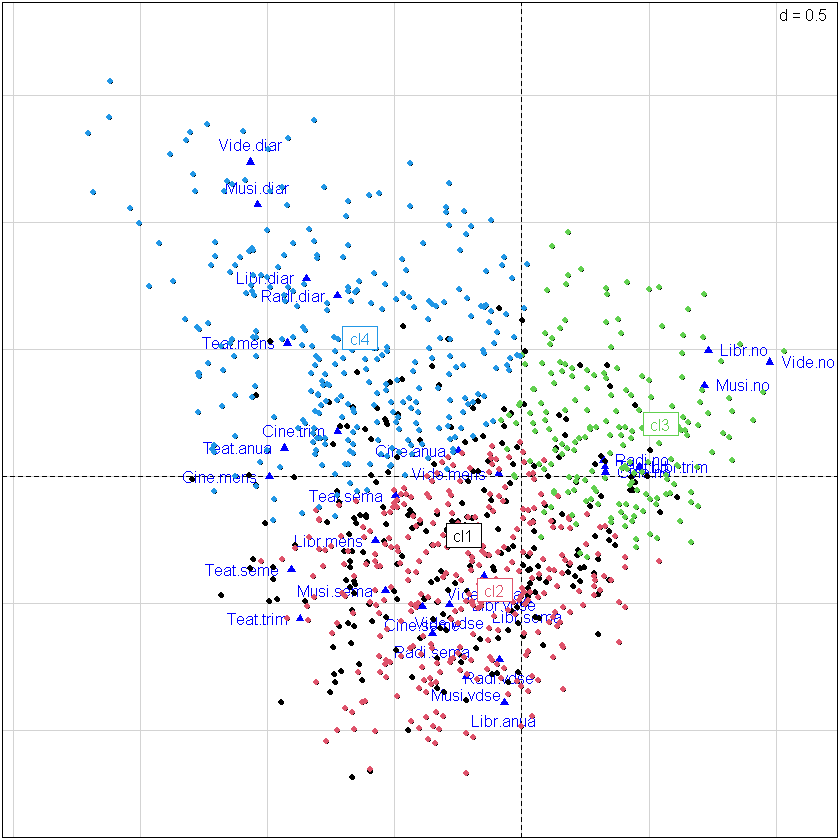
plotFactoClass(fcConCul,roweti="",infaxes="no",cstar=0)
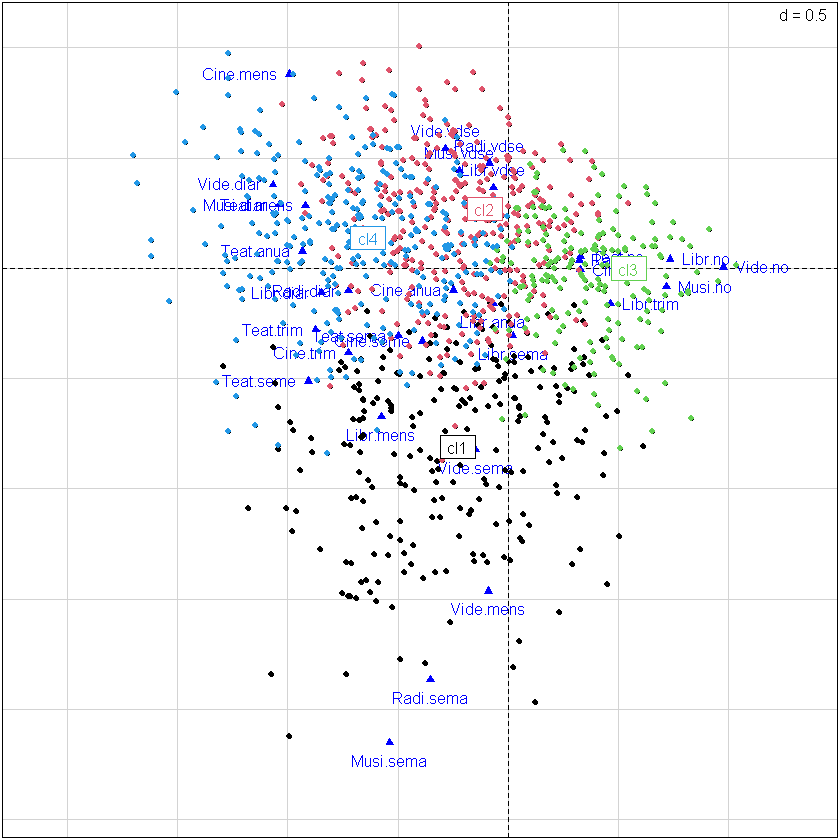
plotFactoClass(fcConCul,x=1,y=3,roweti="",infaxes="no",cstar=0)
Caracterización de las clases con variables ilustrativas#
cluster.carac(Ys,fcConCul$cluster,tipo.v="no",v.lim= 2,dn=3,dm=3,neg=TRUE)
class: 1
Test.Value p.Value Class.Cat Cat.Class Global Weight
Regi.Cent 2.437 0.015 18.0 21.5 16.6 328
Regi.Atla 2.330 0.020 18.3 17.8 13.6 268
Regi.Bogo 2.097 0.036 17.4 19.6 15.7 310
Regi.Orie -3.929 0.000 8.7 14.2 22.8 450
------------------------------------------------------------
class: 2
Test.Value p.Value Class.Cat Cat.Class Global Weight
Estr.3oM 2.375 0.018 37.0 22.0 19.2 378
Regi.Cent -2.178 0.029 27.7 14.3 16.6 328
Estr.0o1 -2.998 0.003 28.8 37.5 42.1 829
------------------------------------------------------------
class: 3
Test.Value p.Value Class.Cat Cat.Class Global Weight
Estr.0o1 8.366 0.000 45.0 54.9 42.1 829
Regi.Orie 5.393 0.000 45.1 29.9 22.8 450
Regi.OrAm 3.766 0.000 43.7 19.9 15.7 309
Edad.a10 -2.085 0.037 31.2 23.4 25.9 510
Estr.2 -3.611 0.000 29.8 33.5 38.8 764
Regi.Atla -4.690 0.000 22.4 8.8 13.6 268
Regi.Bogo -5.146 0.000 22.3 10.1 15.7 310
Estr.3oM -6.429 0.000 20.9 11.6 19.2 378
------------------------------------------------------------
class: 4
Test.Value p.Value Class.Cat Cat.Class Global Weight
Estr.3oM 4.350 0.000 27.2 27.2 19.2 378
Regi.Atla 2.827 0.005 25.4 17.9 13.6 268
Regi.Bogo 2.546 0.011 24.2 19.8 15.7 310
Estr.2 2.015 0.044 21.2 42.7 38.8 764
Regi.Orie -2.473 0.013 15.6 18.5 22.8 450
Regi.OrAm -4.108 0.000 11.3 9.2 15.7 309
Estr.0o1 -5.398 0.000 13.8 30.1 42.1 829


