Tensores
Contents
Tensores#
Introducción
Fuente: Alvaro Montenegro
Introducción#
En esta lección aprenderemos los conceptos básicos de tensores y como los usamos para manipular imágenes usando tensores.
Tensor#
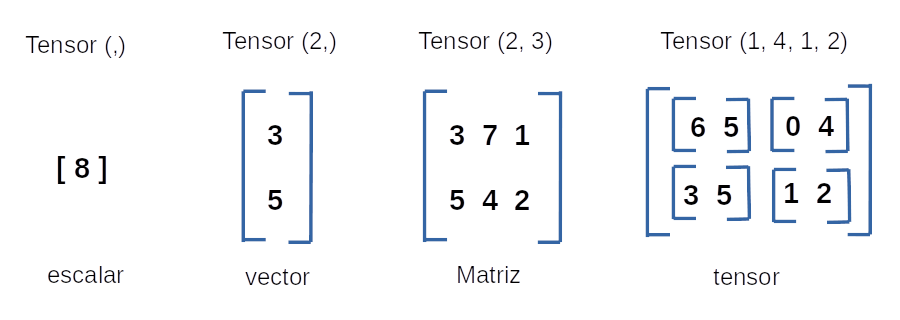
Un tensor es un concepto matemático que generaliza los conceptos de escalares, vectores y matrices.
Fuente: Alvaro Montenegro
En términos muy simples, un tensor es un objeto dinámico (matemáticamente diríamos que es una función entre espacios vectoriales) que vive dentro de una estructura.
Pero no vamos a hacer un tratado matemático aquí.
Lo importante en esta clase es entender que en realidad, escalares, vectores, matrices pueden verse como tensores fijos y eso será suficiente para lo que sigue.
Rango#
Diremos que los escalares tienen rango (shape) 0, los vectores tiene rango 1, las matrices rango 2 y el tensor de la derecha rango 3.
El rango corresponde al número de índices que se requiere para identificar de manera única a cada elemento del tensor.
Observe que por ejemplo, en el último tensor, requiere (fila, columna, cajón).
También podría ser (cajón, fila, columna).
Redes Neuronales#
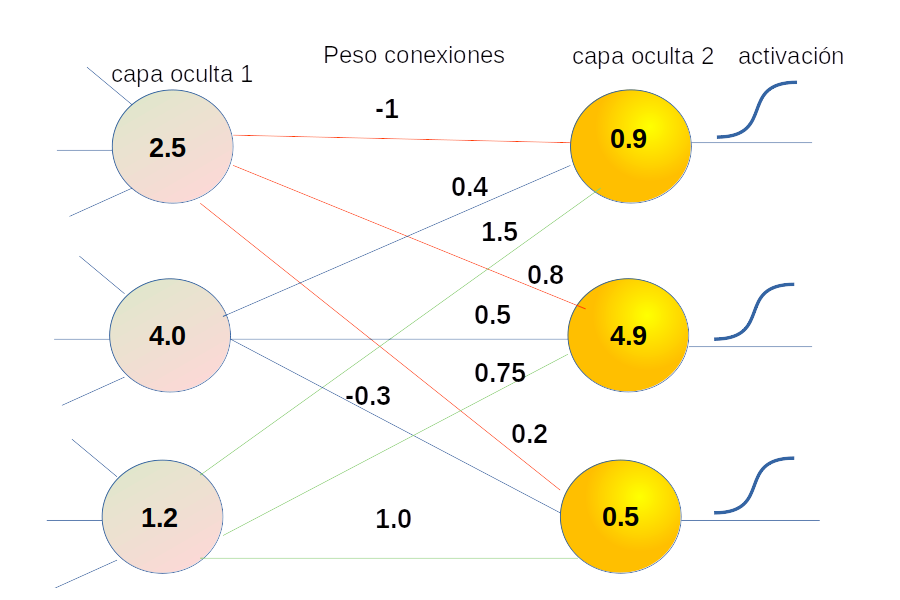
La siguiente imagen muestra el estado en un instante de una una parte oculta de una red neuronal profunda.
Fuente: Alvaro Montenegro
El proceso puede modelarse en forma simplificada usando matrices y vectores como se ve a continuación.
Observe por ejemplo que:
En la fase de entrenamiento de la red neuronal, los pesos de la matriz se van modificando hasta que se encuentra un óptimo local. Este proceso ocurre en toda la estructura de la red.
Por lo que no parece extraño que las GPU y las TPU pasen todo el tiempo haciendo operaciones de este tipo, que al final se reduce a sumas y multiplicaciones.
Por otro lado, lo que ocurre es que los objetos que se procesan no necesariamente son vectores como en el ejemplo, y esto lleva a la necesidad de generalizar los conceptos.
Producto tensorial#
La operación más ejecutada en aprendizaje profundo es el producto tensorial.
Vamos a suponer que cada elemento en los tensores de rango 3 se indexan mediante coordenadas (fila, columna, profundidad) y que los tensores de rango 2 se indexan como (fila, columna).
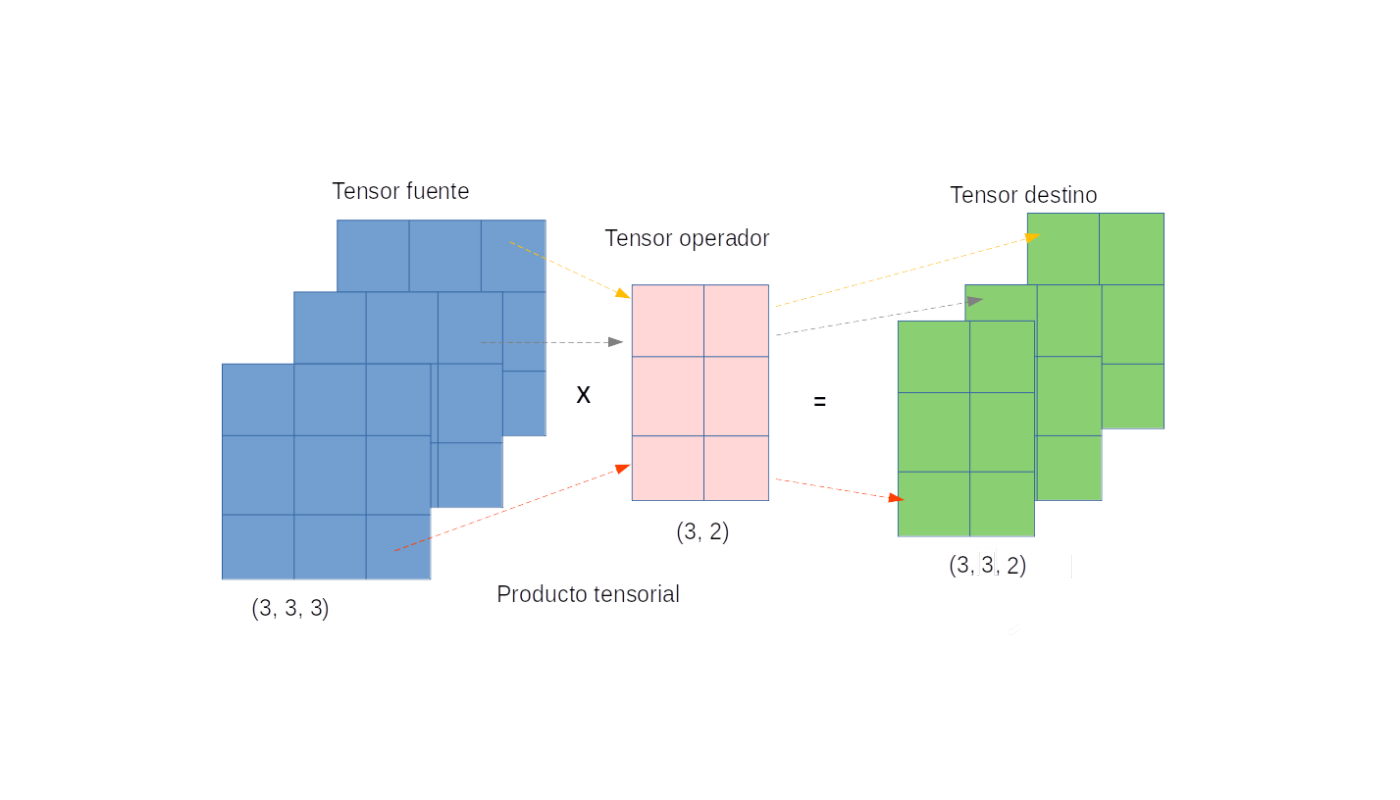
La siguiente imagen ilustra la forma de un producto tensorial.
A la izquierda (azul) se tiene un tensor de tamaño digamos \(n \times p \times s\).
El tensor que está operando en el centro (rosa) es de tamaño \(p \times r\). Este actúa operando en este caso sobre cada capa del tensor de la izquierda haciendo un producto usual de matrices.
Por lo que el tensor resultante (verde) a la derecha tiene tamaño \(n \times r \times s\)

Fuente: Alvaro Montenegro
Explicación del producto#
La explicación del proceso es la siguiente:
Cada capa frontal del tensor azul es multiplica por el tensor rosa y el resultado es colocando como una capa frontal en el tensor resultante (verde).
Cada multiplicación es entre dos matrices (azul * rosa) y el resultado es una matriz (verde).
Cada multiplicación de matrices se hace por la fórmula fila (matriz azul) * columna (matriz rosa)
Vamos por ejemplo a suponer que una capa roja es \( azul = \begin{pmatrix} 1 & 2 & 1\\ 3 & 4 & 1 \\ 4 & 5 & 0\\ \end{pmatrix}\), \(rosa = \begin{pmatrix} 5 & 10\\ 20 & 30 \\ 4 & 1\end{pmatrix}\)
Entonces se tiene que
Imágenes a color#
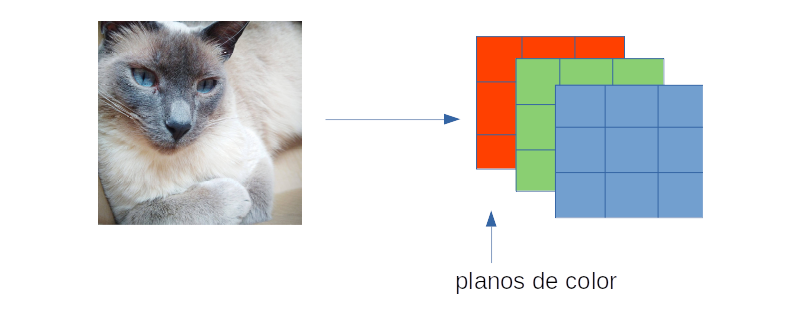
De manera clásica una imagen a color está compuesta de tres colores primarios: rojo (Red), verde (Green) y azul (Blue). Para generar una imagen a color un computador maneja tres planos de color, los cuales son controlados desde tensores tridimensionales. Considere el siguiente ejemplo.
Fuente: Alvaro Montenegro
Cada pixel (punto) de la imagen es representado por una valor numérico en el rango de 0 a 255, o en rango de valores reales entre cero y 1.
Construcción aleatoria de una imagen#
Considere el siguiente código Python.
import numpy as np
I=np.random.randint(0,255,size=(3,10,10))
print(I)
[[[ 71 153 58 134 254 44 191 74 44 241]
[ 72 142 162 105 136 67 116 23 136 87]
[153 20 142 197 10 163 54 117 104 34]
[ 27 138 50 54 217 114 229 41 53 236]
[ 30 139 231 232 115 70 105 74 119 236]
[ 83 156 24 65 139 173 219 91 175 187]
[212 232 138 101 202 22 73 3 222 170]
[194 95 147 252 136 100 114 60 242 103]
[120 113 75 243 12 111 91 53 197 100]
[ 73 53 87 146 190 49 176 96 173 19]]
[[157 41 53 91 160 84 239 222 98 19]
[ 40 247 241 227 5 198 138 164 142 29]
[ 2 77 158 68 122 239 93 167 100 80]
[118 167 247 237 44 243 37 187 225 30]
[250 213 7 122 242 63 90 12 185 128]
[ 3 132 171 58 192 94 98 124 120 46]
[ 91 46 154 220 85 2 154 89 17 199]
[194 80 89 227 4 2 70 11 193 149]
[223 129 76 167 89 232 113 142 5 6]
[ 84 194 44 235 6 125 139 189 238 249]]
[[ 27 128 148 165 81 191 160 233 13 78]
[228 75 111 98 122 17 226 199 125 44]
[ 15 149 143 206 98 97 199 188 171 185]
[183 64 43 141 183 74 211 154 217 147]
[120 207 48 121 168 164 87 39 223 118]
[178 152 101 101 151 120 7 140 251 158]
[248 225 248 233 114 107 25 93 188 159]
[174 25 231 9 211 80 192 98 13 44]
[ 2 89 211 102 108 43 100 13 1 83]
[ 27 41 153 122 253 5 45 108 231 32]]]
Este tensor representa una imagen de tamaño \(10 \times 10\). Son tres planos de color \(10 \times 10\).
Observe que la primera dimensión corresponde a cada plano de color y las restantes dos dimensiones a las intensidades de cada color para cada punto.
Renderizar (dibujar en este caso), nos lleva a la siguiente imagen.
# conda install -c conda-forge matplotlib
import matplotlib.pyplot as plt
plt.imshow(I.T)
plt.show()

Observe que
(I.T).shape
(10, 10, 3)
Porque Python maneja las imágenes en este formato: Fila, columna y plano de color.
Imagen real#
Vamos a trabajar ahora con una imagen real.
import numpy as np
import matplotlib.pyplot as plt
# conda install -c anaconda scikit-image
from skimage import data
from skimage.color import rgb2gray
original = data.astronaut()
grayscale = rgb2gray(original)
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
ax[0].imshow(original)
ax[0].set_title("Original")
ax[1].imshow(grayscale, cmap=plt.cm.gray)
ax[1].set_title("Grayscale")
fig.tight_layout()
plt.show()

Idata=np.array(grayscale)
print("\nLa imagen tiene forma: ",Idata.shape,"\n")
print(Idata)
La imagen tiene forma: (512, 512)
[[5.83434902e-01 4.14859216e-01 2.44058431e-01 ... 4.75007843e-01
4.58213333e-01 4.69121961e-01]
[6.75588235e-01 5.56006667e-01 4.49052941e-01 ... 4.68548627e-01
4.56501176e-01 4.55958431e-01]
[7.66334902e-01 7.00524314e-01 6.49276078e-01 ... 4.76406667e-01
4.62104314e-01 4.53978431e-01]
...
[6.81696471e-01 6.81979216e-01 6.71889020e-01 ... 0.00000000e+00
2.82745098e-04 0.00000000e+00]
[6.74694510e-01 6.68532941e-01 6.64030196e-01 ... 2.82745098e-04
3.92156863e-03 0.00000000e+00]
[6.70482353e-01 6.63189804e-01 6.52838824e-01 ... 0.00000000e+00
3.92156863e-03 0.00000000e+00]]
Planos de color#
Idata = np.array(original)
print("\nLa imagen tiene forma: ",Idata.shape,"\n")
print("\nEscala de Rojos:\n\n",Idata[:511,:511,0],"\n")
print("\nEscala de Verdes:\n\n",Idata[:511,:511,1],"\n")
print("\nEscala de Azules:\n\n",Idata[:511,:511,2],"\n")
La imagen tiene forma: (512, 512, 3)
Escala de Rojos:
[[154 109 63 ... 126 127 120]
[177 144 113 ... 126 127 124]
[201 182 168 ... 125 128 126]
...
[186 188 184 ... 0 0 0]
[186 186 183 ... 2 0 0]
[183 182 185 ... 21 0 1]]
Escala de Verdes:
[[147 103 58 ... 120 120 117]
[171 141 114 ... 118 118 115]
[194 178 165 ... 119 120 116]
...
[169 169 167 ... 0 0 0]
[170 170 168 ... 2 0 0]
[169 167 164 ... 21 0 1]]
Escala de Azules:
[[151 124 102 ... 114 115 106]
[171 143 124 ... 111 112 108]
[193 175 164 ... 113 117 112]
...
[174 177 170 ... 0 0 1]
[176 177 170 ... 3 0 1]
[170 171 176 ... 16 1 1]]
fig, (ax1, ax2,ax3) = plt.subplots(1, 3,figsize=(15,15))
ax1.imshow(Idata[:,:,0],cmap="Reds")
ax1.set_xlabel('Red')
ax2.imshow(Idata[:,:,1],cmap="Greens")
ax2.set_xlabel('Green')
ax3.imshow(Idata[:,:,2],cmap="Blues")
ax3.set_xlabel('Blue')
plt.show()

Manipulación de imágenes#
Intercambia dos planos de color#
import numpy as np
import matplotlib.pyplot as plt
from skimage import data
from skimage.color import rgb2gray
original = data.astronaut()
Idata_m = Idata
Idata_m[:,:,0], Idata_m[:,:,2] = Idata_m[:,:,2], Idata_m[:,:,0]
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
ax[0].imshow(original)
ax[0].set_title("Original")
ax[1].imshow(Idata_m)
ax[1].set_title("Modificada")
fig.tight_layout()
plt.show()

Suma una constante a la imagen#
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
k = 10
ax[0].imshow(original)
ax[0].set_title("Original")
ax[1].imshow(original + k)
ax[1].set_title("Modificada")
fig.tight_layout()
plt.show()

fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
k = 2
ax[0].imshow(original)
ax[0].set_title("Original")
ax[1].imshow(original //k)
ax[1].set_title("Modificada")
fig.tight_layout()
plt.show()

Idata_m = Idata
Idata_m[:,:,0 ]=0
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
ax[0].imshow(original)
ax[0].set_title("Original")
ax[1].imshow(Idata_m)
ax[1].set_title("Modificada")
fig.tight_layout()
plt.show()

Idata
array([[[ 0, 147, 151],
[ 0, 103, 124],
[ 0, 58, 102],
...,
[ 0, 120, 115],
[ 0, 117, 106],
[ 0, 119, 110]],
[[ 0, 171, 171],
[ 0, 141, 143],
[ 0, 114, 124],
...,
[ 0, 118, 112],
[ 0, 115, 108],
[ 0, 116, 105]],
[[ 0, 194, 193],
[ 0, 178, 175],
[ 0, 165, 164],
...,
[ 0, 120, 117],
[ 0, 116, 112],
[ 0, 114, 109]],
...,
[[ 0, 170, 176],
[ 0, 170, 177],
[ 0, 168, 170],
...,
[ 0, 0, 0],
[ 0, 0, 1],
[ 0, 0, 0]],
[[ 0, 169, 170],
[ 0, 167, 171],
[ 0, 164, 176],
...,
[ 0, 0, 1],
[ 0, 1, 1],
[ 0, 0, 0]],
[[ 0, 167, 172],
[ 0, 165, 169],
[ 0, 162, 171],
...,
[ 0, 0, 0],
[ 0, 1, 1],
[ 0, 0, 0]]], dtype=uint8)
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
ax[0].imshow(original)
ax[0].set_title("Original")
ax[1].imshow(255 - Idata)
ax[1].set_title("Modificada")
fig.tight_layout()
plt.show()

Colocar dos imagenes en un tensor#
Esta es una forma para organizar conjuntos de imágenes en un único tensor
original= np.expand_dims(original,axis=0)
original.shape
(1, 512, 512, 3)
Idata_m= np.expand_dims(Idata_m,axis=0)
images = np.concatenate((original, Idata_m),axis=0)
images.shape
(2, 512, 512, 3)
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
ax = axes.ravel()
ax[0].imshow(images[0])
ax[0].set_title("Original")
ax[1].imshow(images[1])
ax[1].set_title("Modificada")
fig.tight_layout()
plt.show()

Trasformaciones afines#
En este ejemplo usaremos la librería OpenCV.
Esta es la imagen original tomada de omes-va.com. Código tomado del mismo sitio.
import numpy as np
import cv2
image = cv2.imread('../Imagenes/ave.jpeg')
#cv2.imshow('Imagen de entrada',image)
cv2.waitKey(0)
cv2.destroyAllWindows()
Translación#
Tx, representa el desplazamiento en x.
Ty, representa el desplazamiento en y.
# Translación
ancho = image.shape[1] #columnas
alto = image.shape[0] # filas
# Traslación
M = np.float32([[1,0,100],[0,1,150]])
imageOut = cv2.warpAffine(image,M,(ancho,alto))
cv2.imshow('Imagen de entrada',image)
cv2.imshow('Imagen de salida',imageOut)
cv2.waitKey(0)
cv2.destroyAllWindows()
Rotación#
\(\theta\) representa el ángulo de rotación. En este ejemplo \(\theta = \pi/4\) 0 lo que es lo mismo \(45^o\).
# rotación
ancho = image.shape[1] #columnas
alto = image.shape[0] # filas
M = cv2.getRotationMatrix2D((ancho//2,alto//2),15,1)
imageOut = cv2.warpAffine(image,M,(ancho,alto))
cv2.imshow('Imagen de entrada',image)
cv2.imshow('Imagen de salida',imageOut)
cv2.waitKey(0)
cv2.destroyAllWindows()
image.shape
(426, 640, 3)


