Distribuciones de probabilidad continuas#

Introducción#

En esta lección se introducen las distribuciones de probabilidad continuas. Además se introducen los conceptos de información en distribuciones continuas y la entropía diferencial.

Al empezar se introduce el concepto de variable aleatoria continua y la distribución normal. Si no recuerda el concepto de integral de una función en un intervalo, puede imaginar que una integral es aproximadamente un promedio de los valores de la función en un determinado intervalo.

Por ejemplo si una función \(h(x)\) está definida en un intervalo digamos \([a,b]\), entonces la integral de \(h\) en ese intervalo es aproximadamente una suma pesada:

\[ \int_{a}^{b} h(x)dx \approx p_1f(x_1) + p_2f(x_2) + \ldots + p_nf(x_n), \]

para algunos pesos \(p_1,\ldots,p_n\) y algunos valores \(x_1,\ldots,x_n\).

Esto es todo lo que necesitamos saber para seguir la lección. Calcular una integral puede ser muy complicado, pero en esta lección solamente requerimos tener presente la ecuación anterior.

Variables aleatorias continuas#

Supongamos que se mide con una herramienta de precisión el diámetro de la cabeza de un tornillo salido de un proceso de producción. Es conocido que cada tornillo producido puede tener pequeñas diferencias de tamaño. Esto se debe en general a la forma como cada tornillo es procesado. Las máquinas que los producen por lo general pierden precisión por el uso.

Otro ejemplo menos preciso pero más cercano a nosotros es medir la estatura de las personas. En este caso los instrumentos son mucho menos precisos.

Ejercicio#

¿Puede indicar otros ejemplos?

Si se define \(X\) como la medida en cada caso, es claro que \(X\) es una variable aleatoria, puesto que al realizar los experimentos (en este caso las mediciones), no se puede predecir con total precisión, cual será el valor medido en cada experimento.

Por otro lado \(X\) tiene una característica diferente a las variables aleatorias discretas estudiadas con anterioridad. Sus posibles valores ahora no pueden enumerarse. Dentro de un rango razonable es posible obtener como resultado cualquier número real dentro de ese rango. En este caso se dice que la variable aleatoria es continua.

Para las variables aleatorias continuas no existe función de probabilidad, debido a que ahora para cada valor posible no es posible asociar una probabilidad diferente de cero. En este caso se toman intervalos tan grandes o pequeños como sea posible y a estos intervalos se les asigna una medida de probabilidad.

Función de densidad de probabilidad#

La función de densidad de probabilidad, en adelante función de densidad, es el homólogo de la función de probabilidad. Se trata entonces de una función integrable no negativa, en donde el área bajo la curva es 1.

El ejemplo más simple es la distribución uniforme en el intervalos \([0,1]\). En este caso la función de densidad es \(g(x)=1\). Note que en este caso se tiene que

\[ \int_0^1 g(x)dx = \int_0^1 1 dx= x|_{x=0}^{x=1} = 1-0 =1. \]

Esta distribución se llama uniforme porque cada subintervalo de \([0,1]\) tiene exactamente la misma probabilidad. Por ejemplo los intervalos \([0.1,0.3]\) y \([0.5,0.7]\) tiene cada uno medida de probabilidad 0.2. En este caso, la medida de probabilidad coincide con la medida de longitud que usamos a diario para medir longitudes, como por ejemplo, el frente de una casa.

Esperanza matemática y varianza#

Las definiciones en este caso son generalizaciones a las estudiadas para el caso discreto, cambiado los promedios por integrales. Entonces se tiene que si \(X\) es una variable aleatoria continua con densidad dada por \(g(x)\), se tiene que la esperanza matemática (o valor esperado) y la varianza son dadas por

\[\begin{split} \begin{align} \mathbb{E}[X] &= \mu_X=\int xg(x)dx\\ \text{Var}[X] &= \int( x - \mu_X)^2g(x)dx\\ \end{align} \end{split}\]

Los límites de las integrales dependen del tipo de distribución. De acuerdo con lo mencionado en la introducción, en relación con el concepto de integral, podemos conservar las interpretaciones de la media y la varianza del caso discreto.

La media es aproximadamente el valor promedio de la variable aleatoria que se obtiene si se realiza muchas veces el experimento aleatorio y se calcula la medida dada por la variable aleatoria.

Por otro lado la varianza mide el grado de predictibilidad de la variable aleatoria. Entonces, aunque no son conceptos exáctamente equivalentes podemos mantener las interpretaciones. Lo mismo ocurre con los conceptos de la teoría de información.

Ejercicio#

Verifique la afirmación anterior.

Ayuda

\(\text{Prob}[0.5,0.7] =\int_{0.5}^{0.7} g(x)dx \).

Distribución normal#

La distribución normal es la distribución más importante de toda la estadística. Esto no solamente se debe a su aplicación en gran cantidad de problemas, sino porque es la distribución límite de muchas sucesiones de distribuciones que aparecen con frecuencia. No entraremos en detalles técnicos. Solamente vamos a indicar la expesión de la función de densidad y veremos como calcular algunas probabilidades.

La densidad de la distribución normal tiene la expresión:

\[ g(x) = \sqrt{\tfrac{1}{2\pi\sigma^2}} e^{-\tfrac{(x-\mu)^2}{2\sigma^2}} \]

La expresión es un poco intimidante, pero su uso con la ayuda de Python es muy fácil. Vamos primero a dar las expresiones para la media y la varianza de la distribución normal

  1. Los parámetros de la distribución normal son \(\mu\) y \(\sigma^2\).

  2. La función \(g(x)\) es simétrica alrededor de \(\mu_X\).

Además si \(X\) es una variable aleatoria con distibución normal, que escribiremos \(X\sim \mathcal{N}(\mu,\sigma^2)\), entonces

  1. \(\mathbb{E}[X] = \mu\)

  2. \(\text{Var}[X] = \sigma^2\)

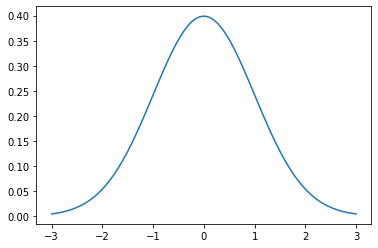
El siguiente es un gráfico de la densidad de una distribución normal. Por favor revise el código Python cuidadosamente y haga cambios en los parámetros para ver el efecto en la densidad.

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import math

mu = 0
variance = 1
sigma = math.sqrt(variance)
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
plt.plot(x, stats.norm.pdf(x, mu, sigma))
plt.show()
../../_images/Prob_Distribuciones_continuas_19_0.png 
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider, Button



# Parametros iniciales
mu = 0
variance = 1
sigma = math.sqrt(variance)
t = np.linspace(mu - 3*sigma, mu + 3*sigma, 1000)
# Crear la figura y el line que manipulatemos
fig, ax = plt.subplots()
line, = plt.plot(t, stats.norm.pdf(t, mu, sigma), lw=2)

# Ajustar el grafico para dejar espacio para los deslizadores
plt.subplots_adjust(left=0.25, bottom=0.25)

# Make a horizontal slider to control mu.
axfreq = plt.axes([0.25, 0.1, 0.65, 0.03])
mu_slider = Slider(
    ax=axfreq,
    label='Mu',
    valmin=-3,
    valmax=3,
    valinit=mu,
)

# Make a vertically oriented slider to control sigma
axamp = plt.axes([0.1, 0.25, 0.0225, 0.63])
sigma_slider = Slider(
    ax=axamp,
    label="Sigma",
    valmin=0,
    valmax=5,
    valinit=sigma,
    orientation="vertical"
)


# The function to be called anytime a slider's value changes
def update(val):
    line.set_ydata(stats.norm.pdf(t, mu_slider.val, sigma_slider.val))
    fig.canvas.draw_idle()


# register the update function with each slider
mu_slider.on_changed(update)
sigma_slider.on_changed(update)

# Create a `matplotlib.widgets.Button` to reset the sliders to initial values.
resetax = plt.axes([0.8, 0.025, 0.1, 0.04])
button = Button(resetax, 'Reset', hovercolor='0.975')


def reset(event):
    mu_slider.reset()
    sigma_slider.reset()
button.on_clicked(reset)

plt.show()

Ejercicio#

Consulte como calcular usando Python la medida de probabilidad de los siguientes intervalos, si se asume una distribución normal con media 10 y varianza 1.

  1. \([5,15]\).

  2. \([0,\infty]\)

  3. \([8,11]\)

Ayuda

\(\text{Prob}[a,b] = \text{Prob}[-\infty,b] - \text{Prob}[-\infty,a]\).

# Prob[−∞,𝑎] .
import scipy.stats as stats
import math
a = 8
mu = 10
var = 1
sigma = math.sqrt(var)
prob_inf_a = stats.norm.cdf(a, mu, sigma)
prob_inf_a

0.022750131948179195

Función de distribución acumulada#

Dada una distribución con densidad \(g(x)\), su función de distribución acumulada evaluada en \(x\) se define mediante la función \(G\) dada por:

\[ G(x) = \int_{-\infty}^{x}g(x)dx \]

Observe que en consecuencia si \(G\) es una función de distribución acumulada se tiene que para cualquier intervalo \([a,b]\)

\[ \text{Prob}[a,b] = G(b) - G(a) = \int_{-\infty}^{b}g(x)dx - \int_{-\infty}^{a}g(x)dx = \text{Prob}[-\infty,b] - \text{Prob}[-\infty,a]. \]

Información de distribuciones continuas#

La siguiente gráfica muestra las funciones de información (diferencial), definida por \(-\log g(x)\). La información diferencial representa el grado de sorpresa de observar el valor en cada punto.

Tanto la distribución de Student(0,1,df=10) como la doble exponencial(0,1) tienen valores sorpresa muy por debajo de lo normal(0,1) en los rangos (-6, 6). Esto significa que los valores atípicos tendrán menos efecto en el log-posterior de los modelos que usan estas distribuciones. Una línea de regresión necesitaría moverse menos para incorporar esas observaciones, ya que la distribución del error no las considerará inusuales.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
from scipy.stats import t
from scipy.stats import laplace
#
fig, ax = plt.subplots(1, 1,figsize=(12, 8))
plt.title('Funciones de información',fontsize=14)

x = np.linspace(-6,6,300)
#
y_laplace = -np.log(laplace.pdf(x))
ax.plot(x, y_laplace, 'g-', lw=2, alpha=0.6, label='laplace pdf')
#
y_norm = -np.log(norm.pdf(x))
ax.plot(x, y_norm, 'r-', lw=2, alpha=0.6, label='norm pdf')
#
y_student_t = -np.log(t.pdf(x, df=10))
ax.plot(x, y_student_t, 'b-', lw=2, alpha=0.6, label='student-t pdf')

#
plt.xlabel('$x$',fontsize=14)
plt.ylabel('$I(x) = -\log \ f(x)$',fontsize=14)
plt.legend()
plt.show()

Ejercicio#

Revise las distribuciones de Laplace y \(t\)-student utilizadas arriba.

Entropia diferencial#

La entropía de Shannon está restringida a variables aleatorias que toman valores discretos. La fórmula correspondiente para una variable aleatoria continua con función de densidad de probabilidad \( f(x) \) con soporte (dominio) finito o infinito \( \mathbb{X}\) en la línea real se define por analogía, utilizando la forma anterior de la entropía como una esperanza:

\[h[f]= E [-\ln(f(x))]=-\int_{\mathbb {X}}f(x)\ln(f(x))dx.\]

Esta fórmula generalmente se conoce como entropía continua, o entropía diferencial.

Aunque la analogía entre ambas funciones es sugestiva, debe establecerse la siguiente pregunta:

¿Es la entropía diferencial una extensión válida de la entropía discreta de Shannon?

La entropía diferencial carece de una serie de propiedades que la entropía discreta de Shannon tiene, incluso puede ser negativa.

  • \( \leadsto \) Se puede demostrar que la entropía diferencial no es un límite de la entropía de Shannon para \( n \to \infty \).

Por otro lado, los conceptos y definiciones de la entropía de Shannon se traducen con la misma interpretación al caso continuo. Las sumas ahora son integrales. Así tenemos en el caso continuo que:

  1. Entropía conjunta: \(H(X,Y) = -\int \int f(x,y)\ln f(x,y) dx dy\).

  2. Entropía condicional: \(H(Y|X)= -\int\int f(x,y)\ln p(y|x) dx dy\).

  3. Infromación mutua: \(\mathfrak{M}(X,Y) = \int \int f(x,y)[\ln f(x,y) - \ln f_X(x)f_Y(y)]dx dy\).

Entropía de la familia normal#

Se puede verificar que la entropía diferencial de la familia de distribuciones normales está dada por:

\[ Entropia_{normal} = \tfrac{1}{2} \ln(2\pi e\sigma^2 ) \]

Se observa entonces que tanto la varianza \(\sigma^2\) como la entropía \(\tfrac{1}{2} \ln(2\pi e\sigma^2) \) son funciones crecientes. A mayor valor de \(\sigma\), mayor entropía y viceversa. Así una variable aleatoria que tiene distribución normal es mas predecible entre menor es su varianza.

La figura muestra la entropía y la varianza en función de \(\sigma\) para la familia normal.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
from scipy.stats import t
from scipy.stats import laplace
#
fig, ax = plt.subplots(1, 1,figsize=(12, 8))
plt.title('Entropía y varianza en la familia normal como función de $\sigma$',fontsize=14)

sigma = np.linspace(0.4,2,300)
#
varianza = sigma**2
ax.plot(sigma, varianza, 'g-', lw=2, alpha=0.6, label='varianza')
#
entropia = 0.5*np.log(2*np.pi*np.e*sigma**2)
ax.plot(sigma, entropia, 'r-', lw=2, alpha=0.6, label='entropía')
#
plt.xlabel('$\sigma$',fontsize=14)
plt.ylabel('$entropía = 0.5\cdot\log (2\pi e \sigma^2)$',fontsize=14)
plt.legend()
plt.show()