Mapas Auto-organizados (SOM)
Contents
Mapas Auto-organizados (SOM)#
Instalar Minisom#
#!pip install minisom
Introducción#

El profesor Kohonen ha hecho importantes investigaciones y contribuciones en el campo de las redes neuronales artificiales incluyendo el algoritmo LVQ y su más famosa contribución: los mapas auto organizados (también conocidas como redes de Kohonen o SOMs), así como también a las teorías fundamentales de la memoria asociativa distribuida y mapas asociativos óptimos, entre otros. La mayor parte de sus investigaciones las ha llevado a cabo en la que actualmente es la Universidad Aalto y ha recibido varios premios en reconocimiento a sus logros científicos
Teuvo Kohenen. Fuente: Wikipedia
Mapas cerebrales#
Areas del cerebro. Fuente: Self-Organizing-Maps
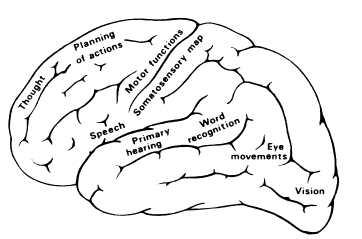
Las diversas áreas del cerebro, especialmente de la corteza cerebral, están organizadas de acuerdo con diferentes modalidades sensoriales:
Tareas especializadas: control del habla.
Señales sensoriales (visuales, auditivas, somatosensoriales).
…
Entre las áreas sensoriales primarias (10% del área cortical) hay áreas asociativas, en las que convergen señales de diferentes modalidades.
\(\leadsto\) Es posible distinguir tres tipos de mapas:
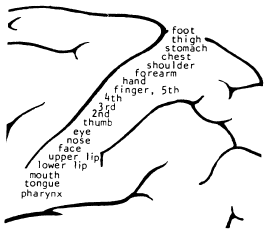
Mapas de habilidades característica específicas, cuya ubicación espacial no se correlaciona con ningún valor de característica.
Proyección anatómica sobre alguna superficie receptora . Por ejemplo: cortezas somáticas visuales.
Mapas ordenados de alguna característica abstracta, para la cual no existe una superficie de repetición. Por ejemplo, el color en el área visual.
Mapa somatotópico. Fuente: Self-Organizing-Maps
\(\leadsto\) Las principales estructuras de las redes cerebrales están determinadas genéticamente. Sin embargo, las proyecciones sensoriales se ven afectadas por la experiencia. Por ejemplo, después de la ablación de órganos sensoriales o tejidos cerebrales o la privación sensorial a una edad temprana, algunas proyecciones no se desarrollan.
Aprendizaje competitivo#
Un orden topográfico o anatómico puro de las conexiones neuronales podría explicarse fácilmente como sigue.
Los axones de las células neurales, cuando crecen hacia sus destinos, pueden ser mantenidos separados por las estructuras celulares, y el destino se encuentra siguiendo la acción de los marcadores químicos.
Mapa tonotópico. Fuente: Self-Organizing-Maps
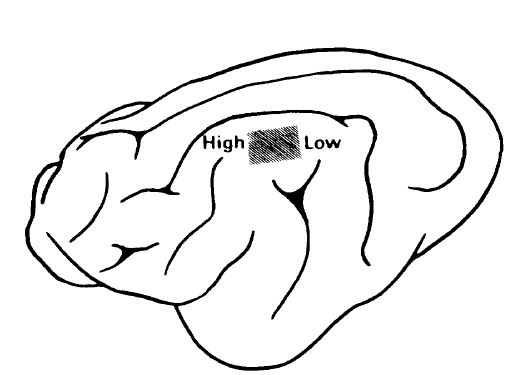
Sin embargo, existe algo de confusión, porque estas conexiones no siempre son una a una, debido a que también existen las estaciones de procesamiento de las rutas de transmisión de señal (núcleos) en las que se mezclan las señales. Por ejemplo, en la corteza auditiva existe el mapa tonotópico de frecuencia acústica de tonos percibidos.
\(\leadsto\) Para concluir: en el cerebro existe un orden espacial y una organización significativa de las funciones cerebrales.
Estos hechos clave fueron los cimientos que Kohonen utilizó para imaginar sus mapas autoorganizados.
A continuación se introducen los conceptos clave usado en la construcción de un SOM.
Cuantización vectorial#
Vector Quantization (Cuantificación Vectorial) es una técnica por la cual el espacio de entradas es dividido en un número determinado de regiones y para cada una de ellas es definido un vector que la caracteriza. Un espacio continuo tiene que ser discretizado. La entrada al sistema son vectores n-dimensionales y la salida es una representación discreta del espacio de entradas. El método Vector Quantization (LVQ) fue originalmente desarrollado por Linde (1980) y Gray (1984). Y como una herramienta para compresión de datos por Gersho y Gray,1992.
Es una técnica usada para reducir la dimensionalidad de datos. Los datos originales constituyen un conjunto de vectores de dimensión \(n\). Estos vectores son mapeados en un conjunto más pequeño de valores llamado codebook o libro de códigos. Tales valores son usados para almacenamiento o transmisión de información, con alguna pérdida.
En el proceso de entrenamiento, los valores del codebook son re-trasladados a valores de codebook que representan a vectores que son cercanos en los datos originales.
Aprendizaje de cuantización vectorial#
Learning Vector Quantization (LVQ) es un método para el entrenamiento competitivo de una manera supervisada. Una capa competitiva automáticamente aprenderá a clasificar automáticamente vectores de entrada. Sin embargo, las clases que la capa competitiva encuentra dependen únicamente de los vectores de entrada. Si dos vectores de entrada son muy similares, la capa competitiva probablemente los colocara en la misma clase. No existe mecanismo en el diseño de una capa competitiva para dictaminar si cualquiera de los vectores de entrada están la misma clase o no. Las redes LVQ aprenden a clasificar vectores de entrada en clases seleccionadas por el usuario. Kohonen, diseñó versiones supervisadas de este método, para problemas de clasificación adaptativa de patrones.
Matemáticamente, LVQ es un método de aproximación de señales en el cual se busca elaborar una aproximación cuantizada de la distribución de los vectores de entrada. \(x \in \mathfrak {R}^n \), usando un conjunto finito de códigos llamado codebook. Denotemos a los elementos del codebook como \(m_i \in \mathfrak {R} ^n, \quad i = 1,2, \ldots, k \) .
Supongamos que ya he ha eligido el codebook. Aproximar el vector \(x\) significa encontrar el vector \(m_c\) en el codebook más cercano a \(x\) (en el espacio de entrada), generalmente usando la métrica euclidiana. Es decir, se busca encontrar \(m_c\) tal que
\(\leadsto\) Realmente, no es necesario utilizar la métrica euclidiana. Si existe una matriz de índices de similitud para medir la similitud entre los elementos de la muestra, el algoritmo puede usar esta medida de similitud para calcular la aproximación.
Algoritmo K-means#
Un algoritmo general que se puede utilizar para calcular un codebook a partir de una muestra es el algoritmo k-means. Este es un algoritmo de tipo experanza-maximización (EM).
Supongamos que tenemos un conjunto de datos \( X = \{x_1, \ldots, x_N; \quad x_i \in \mathfrak {R} ^ n \} \).
El objetivo es dividir el conjunto de datos en un número de clústeres de \(K\), para un valor de \( K \) dado.
Denotemos por \( m_k, k = 1, \ldots, K \) al vector de codebook asociado con el grupo \( k \)-th. Para cada punto \( x_n \) introducimos un vector de variables binarias \( r_{nk} \in \{0,1 \} \), donde \( k = 1, \ldots, K \), la indica a cuál de los \( K \) clústeres está asignado el punto \( x_n \).
La función objetivo (pérdida) se define como
Intuitivamente, esperamos que cada grupo contenga un conjunto de puntos cuyas distancias entre puntos sean pequeñas en comparación con las distancias a puntos fuera del grupo.
El algoritmo#
Escoger aleatoriamente algunos valores \(m_k\).
Paso E. Para cada \(x_n\) sea \(r_{nk}=1\), tal que \(k = \underset{i}{arg min} \{ ||x -m_i||\), and \(r_{nl}=0\) para \(l\ne k\).
Paso M. La función objetivo \(J\) es cuadrática, así que solamente tiene un mínimo. El extremo se puede calcular directamente minimizando \(J\) para obtener
Los pasos 2 y 3 se repiten hasta convergencia.
Teselación de Voronoi#
La siguiente figura ejemplifica un espacio bidimensional donde un número finito de libro de códigos o vectores de referencia se muestra como puntos, correspondientes a sus coordenadas. Este espacio está dividido en regiones, delimitado por líneas (en general hiperplanos) de modo que cada partición contiene un vector de referencia que es el vecino más cercano en promedio a cualquier vector dentro de la misma partición. Estas líneas constituyen la teselación de Voronoi.
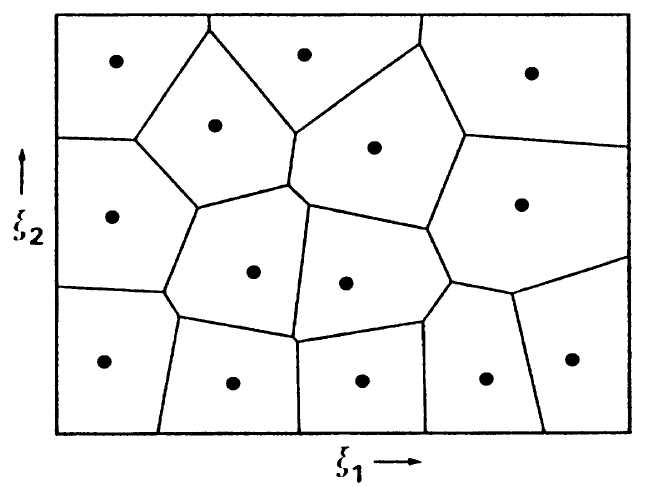
Teselación de Voronoi
Fuente: Self-Organizing-Maps
Conjunto de Voronoi#
Se dice que todos los vectores \( x \) que tienen un vector de referencia particular como su vecino más cercano en la partición correspondiente de la teselación de Voronoi constituyen el conjunto de Voronoi.
El propósito con los mapas auto-organizados (SOM) es construir una especie de teselación de la nube de puntos de entrada.
Mapas Auto-Organizados de Kohonen (SOM)#
Los mapas auto organizados (SOM), también conocidos como mapas de Kohonen, son un tipo de redes neuronales artificiales capaces de convertir relaciones estadísticas complejas y no lineales entre elementos de datos de alta dimensión en relaciones geométricas simples en una grilla de baja dimensión.
En un SOM, las neuronas están organizadas en una grilla, por lo general bidimensional, aunque puede ser de mayor dimensión, y cada neurona está completamente conectada a todos los nodos de origen en la capa de entrada. Una ilustración Matias Carrasco Kind y Robert J. Brunner es la siguiente

Estructura de construcción del mapa autoorganizado
Fuente: Matias Carrasco Kind y Robert J. Brunner
La idea central de Kohonen fue preservar hasta donde fuera posible la estructura topológica de los datos. Es decir, es busca una representación de los datos en la grilla de las neuronas de tal manera que las distancias relativas de los puntos se preservan en la grilla.
Entonces se predefine la grilla de neuronas y el procedimiento busca asignar una celda de la grilla, es decir una neurona, a cada punto de entrada.
La siguiente imagen ilustra como un SOM trata de representar a un conjunto de puntos. En la derecha se dibujan los puntos en la grilla. Se observa una celda (neurona) puede representar a varios puntos. En otras palabras, la proyección no es 1:1, debido a que en general habrá muchos más puntos de datos que neuronas. También puede ocurrir que algunas neuronas no reciban datos proyectados en ella.
En la imagen las neuronas estan representadas en una grilla de celdas hexagonales. Son usuales también grillas rectangulares y otra representaciones. Para mantener la sencillez, vamos a trabajar con grillas de neuronas bidimensionales.
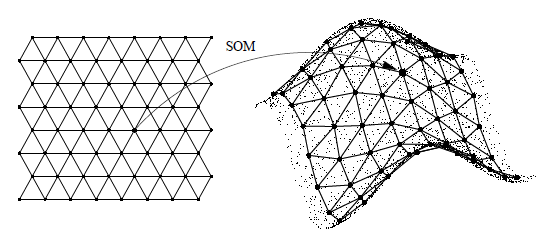
Estructura latente representada por el mapa autoorganizado
Fuente: Self Organizing Maps
Vamos a suponer una configuración de \(N= p\times q\) en la grilla de salida. Cada neurona \(i\) tiene asociada una par de coordenadas enteras, digamos \((i_1,i_2)\) y estan organizadas de tal manera que por ejemplo la neurona más a la izquierda y arriba tiene coordenada (0,0) y la mas a la derecha abajo (p-1, q-1).
Estas coordenadas permiten definir el concepto de función vecindad de una neurona.
Función de vecindad#
Para una neurona, digamos \(i, i=1,\cdots,N\), su función de vecindad define su cercanía con las demás neuronas, la cual es una función de la diferencia entre sus coordenadas.
La función de vecidad más comúnmente usada es el kernel Gaussiano. Por ejemplo para la neurona \(i\), con coordenadas \(n_i=(i_1,i_2)\), su función de vencidad se define por
En el proceso de entrenamiento la función de vecindad cambia en cada paso \(t\). Normalmente esa función de vecindad es cada vez mas restringida. Entonces el parámetro de dispersión \(\sigma\) depende del tiempo en el proceso de entrenamiento. Por esto, en general escribiremos que las función de vecindad depende del tiempo y se escribirá
en donde se espera que \(\sigma^2(t)\to 0\) cuando \(t\to \infty\). Así la vecidad de la neurona se va encogiendo a medida que avanza el entrenamiento.
No olvide que el concepto de vecindad es de las neuronas y su cálculo se basa en la posición de las neuronas en la grilla predefinida para el entrenamiento.
Un ejemplo de cálculo es el siguiente. Supongamos que \(n_i=(2,3)\) y \(n_j=(5,2)\). Además supongamos que \(\sigma^2(t) = 0.2\) para algun paso \(t\) en el entrenamiento. Entonces, se tiene que
debido a que el exponente es cero. Además,
La imagen ilustra el concepto de vecindad.
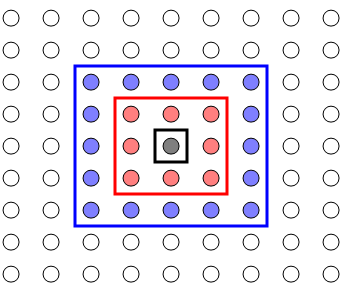
Vecindad en un SOM. Vecindarios (Nc) para una matriz rectangular de unidades de clúster: Nc = 0 entre rectángulos negros, Nc = 1 en rojo y Nc = 2 en azul.
Fuente:
Rata de aprendizaje#
Como es usual en los algoritmos de entrenamiento de redes neuronales se define una rata de aprendizaje que dosifica el tamaño (la norma) del gradiente en el proceso de busqueda de un óptimo. Kohonen se basó inicialmente en la técnica del gradiente descendiente estocástico propuesta por Robbins-Monro .
Ellos propusieron que el paso de cada muestra por el optimizador sea en forma aleatoria y la rata de entrenamiento definida de tal manera que si la rata en el paso \(t\) es \(r(t)\) entonces \(\sum r(t)\to \infty \) y \(\sum r^2(t)<\infty\). Por ejemplo es usual definir \(r(t) = 1/t\).
Pesos sinápticos#
Fuente: Matias Carrasco Kind y Robert J. Brunner

De acuerdo con lo dicho antes, todas las neuronas en la grilla de las neuronas del SOM, se conectan con todas las neuronas a la entrada de los estímulos(datos de entrada). Entonces, si el SOM tiene total \(d\) neuronas y los vectores de entrada tiene dimensión \(n\), lo que implica que hay \(n\) neuronas en la capa de entrada, entonces la fuerza de las conexiones se conocen como peso sináptico y son en total \(n\times d\) pesos. La matriz \(W_{n\times d}\) se usa para representar todos los pesos sinápticos.
El objetivo del proceso de entrenamiento es aprender o estimar estos pesos.
Asignación de los datos a las neuronas en el SOM#
Una vez la red está entrenada, la asignación se hace de la siguiente forma. La fila \(i\) de la matriz \(W\) representa el vector de pesos sinapticos asociado la naurona \(i\). Estos vectores estan en el mismo espacio del conjunto de entrenamiento. Se calcula la distancia geométrica entre el patron \(x\) que está entrando a la red y cada fila de \(W\). La neurona seleccionada es aquella que está a menor distancia. En otras palabras, la neurona \(i\) se selecciona si
Tambien se puede escribir
El algortimo de entrenamiento SOM#
En esta sección se describe el algortimo base desarrollado por Kohonen.
Consideramos un SOM con cuadrícula rectangular bidimensional de \( N \) neuronas. También se pueden usar otras opciones, como cuadrículas hexagonales.
Cada uno de las \(N\) neuronas está parametrizada por un par de coordenadas enteras \((i_1,i_2)\), que corresponde a su posición en la grilla que define el mapa.
Usaremos como función de vecindad, el kernel Gaussiano \(h_{ij}(t)\) definido arriba. Existen muchas posibilidades para definir la función de vecindad.
Sea \(\sigma^2\) un valor inicial para el parámetro de dipersión de la función de vecindad y definimos \(\alpha(t) = 1/t\) como la rata de aprendizaje. Definimos \(\sigma^2(t)= \alpha(t)\sigma^2\).
Hay muchas formas de definir \(\alpha(t)\), que cumplen las condiciones de Robbins-Monro. Ocurre lo mismo con \(\sigma^2(t)\).
El algoritmo de entrenamiento es como sigue.
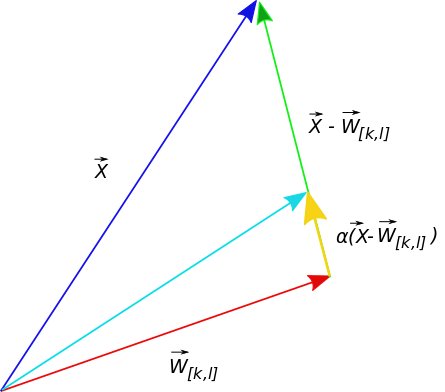
Inicializar los pesos sinápticos de las neuronas de manera aleatoria. Es decir la matriz \(W\) se inicializa aleatoriamente.
Obtenga una muestra aleatoria \(x\) del conjunto de entrenamiento \(X\) y seleccione para este patrón la mejor neurona \(i\) como
En el tiempo \(t+1\) actualice todos los pesos sinápticos
Repita los pasos 2 y 3 hasta completar un número de épocas o cumplir un criterio de convergencia.
Fuente: Luciano da F. Costa, Research gate
Nota
El algoritmo es una generalización del gradiente descendiente estocástico. La presencia de la función de vecindad tiene el efecto de disminuir el efecto del gradiente de acuerdo con la función de vecindad. Las neuronas vecinas más cercanas a la ganadora reciben una valor relativo más grande de actualización. Es decir, neuronas lejanas a la ganadora reciben la señal de actualización cada vez mas atenuada.
Ejemplos con Minisom#
Datos simulados#
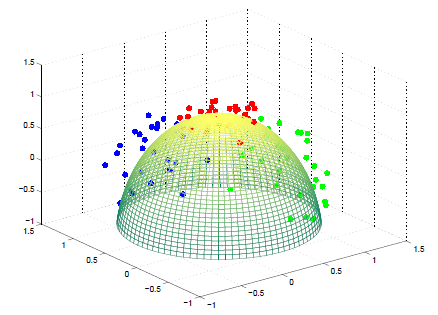
Ejemplo de datos simulados
Fuente: Hastie et al. The elements of the Statistical Learning, Standford, 2008.
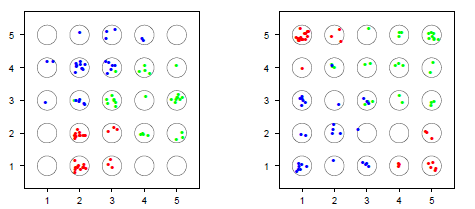
Mapas autoorganizado de los datos simulados. A la izquierda la configuración inicial. A la derecha la configuración final.
Fuente: Hastie et al. The elements of the Statistical Learning, Standford, 2008.
Un primer ejemplo histórico. Gráfico de la pobreza#
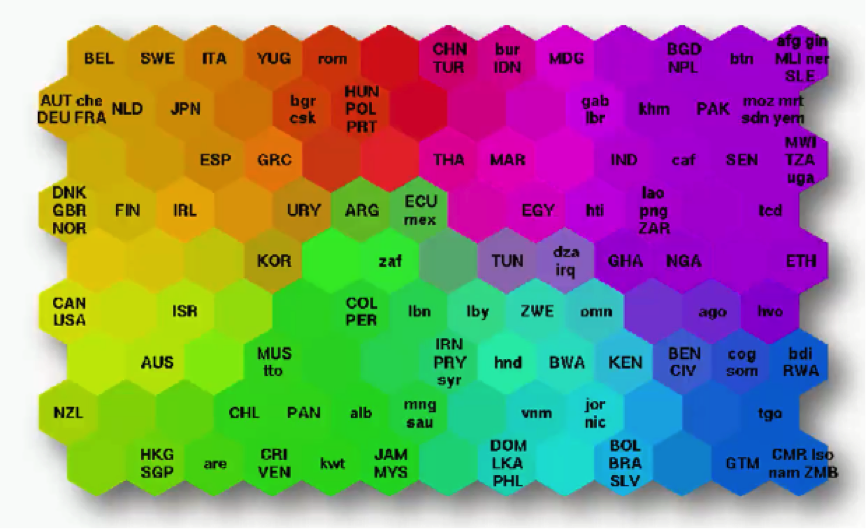
Ejemplo histórico. Mapa de la probreza
Fuente: Kohonen. Poverty map, 1997.
Códigos con Minisom#
import numpy as np
import matplotlib.pyplot as plt
from minisom import MiniSom
Ahora generamos y visualizamos algunos conjuntos de datos con Minisom.
MiniSom implementa dos tipos de entrenamiento.
El entrenamiento secuencial, implementado por el método train_random, donde el modelo se entrena seleccionando muestras aleatorias de sus datos.
El entrenamiento por lotes, implementado por el método train_batch, donde las muestras se seleccionan en el orden en que se almacenan.
Los pesos de la red se inicializan aleatoriamente de forma predeterminada.
Se proporcionan dos métodos adicionales para inicializar los pesos de una manera basada en datos: random_weights_init y pca_weights_init.
Para obtener una descripción general de todas las funciones implementadas en minisom, puede examinar los siguientes ejemplos en Github: https://github.com/JustGlowing/minisom/tree/master/examples
import sys
sys.path.insert(0, '../')
from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
%matplotlib inline
%load_ext autoreload
En lo que sigue, el error de cuantización (quatization error)es el error de reconstrucción y es dado por
$\( q_err = \frac{1}{N} \sum ||x-w_j||^2 \)$,
en donde la suma es sobre los \(x\)’s y en donde \(w_j\) es el correspondiente prototipo de \(x\).
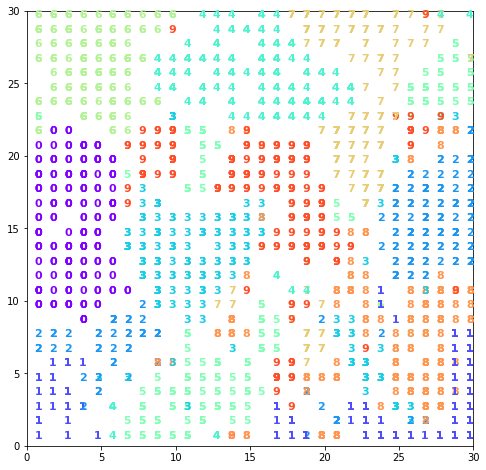
Dígitos a mano alzada#
Eso son son los datos de MNIST. Probablemente es un subconjunto.
import sys
sys.path.insert(0, '../')
from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%load_ext autoreload
The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreload
%autoreload 2
from sklearn import datasets
from sklearn.preprocessing import scale
# load the digits dataset from scikit-learn
digits = datasets.load_digits(n_class=10)
data = digits.data # matrix where each row is a vector that represent a digit.
data = scale(data)
num = digits.target # num[i] is the digit represented by data[i]
digits.data.shape
(1797, 64)
%autoreload 2
from sklearn import datasets
from sklearn.preprocessing import scale
# load the digits dataset from scikit-learn
digits = datasets.load_digits(n_class=10)
data = digits.data # matrix where each row is a vector that represent a digit.
data = scale(data)
num = digits.target # num[i] is the digit represented by data[i]
som = MiniSom(30, 30, 64, sigma=4,
learning_rate=0.5, neighborhood_function='triangle')
som.pca_weights_init(data)
print("Training...")
som.train_random(data, 5000, verbose=False) # random training
print("\n...ready!")
Training...
...ready!
plt.figure(figsize=(8, 8))
wmap = {}
im = 0
for x, t in zip(data, num): # scatterplot
w = som.winner(x)
wmap[w] = im
plt. text(w[0]+.5, w[1]+.5, str(t),
color=plt.cm.rainbow(t / 10.), fontdict={'weight': 'bold', 'size': 11})
im = im + 1
plt.axis([0, som.get_weights().shape[0], 0, som.get_weights().shape[1]])
#Guardar localmente
#plt.savefig('../Imagenes/som_digts.png')
plt.show()
plt.figure(figsize=(10, 10), facecolor='white')
cnt = 0
for j in reversed(range(20)): # images mosaic
for i in range(20):
plt.subplot(20, 20, cnt+1, frameon=False, xticks=[], yticks=[])
if (i, j) in wmap:
plt.imshow(digits.images[wmap[(i, j)]],
cmap='Greys', interpolation='nearest')
else:
plt.imshow(np.zeros((8, 8)), cmap='Greys')
cnt = cnt + 1
plt.tight_layout()
#Guardar localmente
#plt.savefig('../Imagenes/som_digts_imgs.png')
plt.show()

índice de democracia#
import sys
sys.path.insert(0, '../')
%load_ext autoreload
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.patches import Patch
%matplotlib inline
from minisom import MiniSom
from sklearn.preprocessing import minmax_scale, scale
%autoreload 2
The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreload
# download from wikipedia and reorganization
# pre-downloaded file
democracy_index = pd.read_csv('https://raw.githubusercontent.com/AprendizajeProfundo/Libro-Fundamentos/main/Machine_Learning/Datos/democracy_index.csv')
democracy_index.head()
| Unnamed: 0 | rank | country | democracy_index | electoral_processand_pluralism | functioning_of_government | political_participation | political_culture | civil_liberties | category | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | Norway | 9.87 | 10.00 | 9.64 | 10.00 | 10.00 | 9.71 | Full democracy |
| 1 | 1 | 2 | Iceland | 9.58 | 10.00 | 9.29 | 8.89 | 10.00 | 9.71 | Full democracy |
| 2 | 2 | 3 | Sweden | 9.39 | 9.58 | 9.64 | 8.33 | 10.00 | 9.41 | Full democracy |
| 3 | 3 | 4 | New Zealand | 9.26 | 10.00 | 9.29 | 8.89 | 8.13 | 10.00 | Full democracy |
| 4 | 4 | 5 | Denmark | 9.22 | 10.00 | 9.29 | 8.33 | 9.38 | 9.12 | Full democracy |
category_color = {'Full democracy': 'darkgreen',
'Flawed democracy': 'limegreen',
'Hybrid regime': 'darkorange',
'Authoritarian': 'crimson'}
colors_dict = {c: category_color[dm] for c, dm in zip(democracy_index.country,
democracy_index.category)}
country_codes = {'Afghanistan': 'AF',
'Albania': 'AL',
'Algeria': 'DZ',
'Angola': 'AO',
'Argentina': 'AR',
'Armenia': 'AM',
'Australia': 'AU',
'Austria': 'AT',
'Azerbaijan': 'AZ',
'Bahrain': 'BH',
'Bangladesh': 'BD',
'Belarus': 'BY',
'Belgium': 'BE',
'Benin': 'BJ',
'Bhutan': 'BT',
'Bolivia': 'BO',
'Bosnia and Herzegovina': 'BA',
'Botswana': 'BW',
'Brazil': 'BR',
'Bulgaria': 'BG',
'Burkina Faso': 'BF',
'Burundi': 'BI',
'Cambodia': 'KH',
'Cameroon': 'CM',
'Canada': 'CA',
'Cape Verde': 'CV',
'Central African Republic': 'CF',
'Chad': 'TD',
'Chile': 'CL',
'China': 'CN',
'Colombia': 'CO',
'Comoros': 'KM',
'Costa Rica': 'CR',
'Croatia': 'HR',
'Cuba': 'CU',
'Cyprus': 'CY',
'Czech Republic': 'CZ',
'Democratic Republic of the Congo': 'CD',
'Denmark': 'DK',
'Djibouti': 'DJ',
'Dominican Republic': 'DO',
'Ecuador': 'EC',
'Egypt': 'EG',
'El Salvador': 'SV',
'Equatorial Guinea': 'GQ',
'Eritrea': 'ER',
'Estonia': 'EE',
'Ethiopia': 'ET',
'Fiji': 'FJ',
'Finland': 'FI',
'France': 'FR',
'Gabon': 'GA',
'Gambia': 'GM',
'Georgia': 'GE',
'Germany': 'DE',
'Ghana': 'GH',
'Greece': 'GR',
'Guatemala': 'GT',
'Guinea': 'GN',
'Guinea-Bissau': 'GW',
'Guyana': 'GY',
'Haiti': 'HT',
'Honduras': 'HN',
'Hong Kong': 'HK',
'Hungary': 'HU',
'Iceland': 'IS',
'India': 'IN',
'Indonesia': 'ID',
'Iran': 'IR',
'Iraq': 'IQ',
'Ireland': 'IE',
'Israel': 'IL',
'Italy': 'IT',
'Ivory Coast': 'IC',
'Jamaica': 'JM',
'Japan': 'JP',
'Jordan': 'JO',
'Kazakhstan': 'KZ',
'Kenya': 'KE',
'Kuwait': 'KW',
'Kyrgyzstan': 'KG',
'Laos': 'LA',
'Latvia': 'LV',
'Lebanon': 'LB',
'Lesotho': 'LS',
'Liberia': 'LR',
'Libya': 'LY',
'Lithuania': 'LT',
'Luxembourg': 'LU',
'Macedonia': 'MK',
'Madagascar': 'MG',
'Malawi': 'MW',
'Malaysia': 'MY',
'Mali': 'ML',
'Malta': 'MT',
'Mauritania': 'MR',
'Mauritius': 'MU',
'Mexico': 'MX',
'Moldova': 'MD',
'Mongolia': 'MN',
'Montenegro': 'ME',
'Morocco': 'MA',
'Mozambique': 'MZ',
'Myanmar': 'MM',
'Namibia': 'NA',
'Nepal': 'NP',
'Netherlands': 'NL',
'New Zealand': 'NZ',
'North Macedonia': 'NM',
'Nicaragua': 'NI',
'Niger': 'NE',
'Nigeria': 'NG',
'North Korea': 'KP',
'Norway': 'NO',
'Oman': 'OM',
'Pakistan': 'PK',
'Palestine': 'PS',
'Panama': 'PA',
'Papua New Guinea': 'PG',
'Paraguay': 'PY',
'Peru': 'PE',
'Philippines': 'PH',
'Poland': 'PL',
'Portugal': 'PT',
'Qatar': 'QA',
'Republic of China (Taiwan)': 'TW',
'Republic of the Congo': 'CG',
'Romania': 'RO',
'Russia': 'RU',
'Rwanda': 'RW',
'Saudi Arabia': 'SA',
'Senegal': 'SN',
'Serbia': 'RS',
'Sierra Leone': 'SL',
'Singapore': 'SG',
'Slovakia': 'SK',
'Slovenia': 'SI',
'South Africa': 'ZA',
'South Korea': 'KR',
'Spain': 'ES',
'Sri Lanka': 'LK',
'Sudan': 'SD',
'Suriname': 'SR',
'Swaziland': 'SZ',
'Sweden': 'SE',
'Switzerland': 'CH',
'Syria': 'SY',
'Tajikistan': 'TJ',
'Tanzania': 'TZ',
'Thailand': 'TH',
'Timor-Leste': 'TL',
'Togo': 'TG',
'Trinidad and Tobago': 'TT',
'Tunisia': 'TN',
'Turkey': 'TR',
'Turkmenistan': 'TM',
'Uganda': 'UG',
'Ukraine': 'UA',
'United Arab Emirates': 'AE',
'United Kingdom': 'GB',
'United States': 'US',
'Uruguay': 'UY',
'Uzbekistan': 'UZ',
'Venezuela': 'VE',
'Vietnam': 'VN',
'Yemen': 'YE',
'Zambia': 'ZM',
'Zimbabwe': 'ZW'}
feature_names = ['democracy_index', 'electoral_processand_pluralism', 'functioning_of_government',
'political_participation', 'political_culture', 'civil_liberties']
X = democracy_index[feature_names].values
X = scale(X)
size = 15
som = MiniSom(size, size, len(X[0]),
neighborhood_function='gaussian', sigma=1.5,
random_seed=1)
som.pca_weights_init(X)
som.train_random(X, 1000, verbose=False)
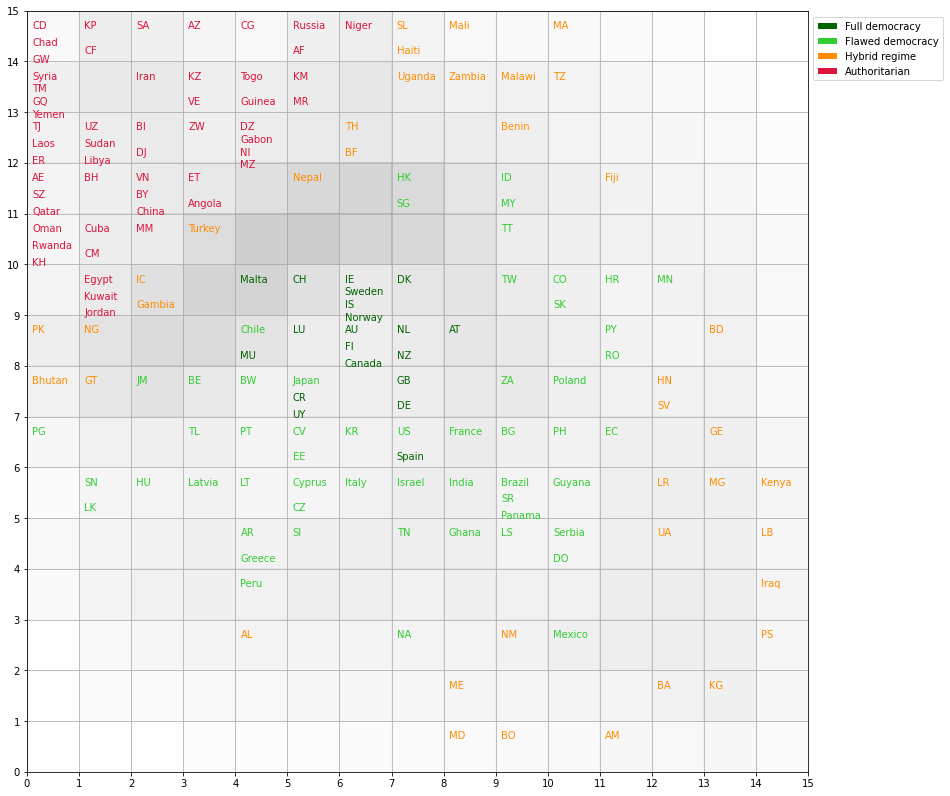
Map of countries#
def shorten_country(c):
if len(c) > 6:
return country_codes[c]
else:
return c
country_map = som.labels_map(X, democracy_index.country)
plt.figure(figsize=(14, 14))
for p, countries in country_map.items():
countries = list(countries)
x = p[0] + .1
y = p[1] - .3
for i, c in enumerate(countries):
off_set = (i+1)/len(countries) - 0.05
plt.text(x, y+off_set, shorten_country(c), color=colors_dict[c], fontsize=10)
plt.pcolor(som.distance_map().T, cmap='gray_r', alpha=.2)
plt.xticks(np.arange(size+1))
plt.yticks(np.arange(size+1))
plt.grid()
legend_elements = [Patch(facecolor=clr,
edgecolor='w',
label=l) for l, clr in category_color.items()]
plt.legend(handles=legend_elements, loc='center left', bbox_to_anchor=(1, .95))
plt.show()
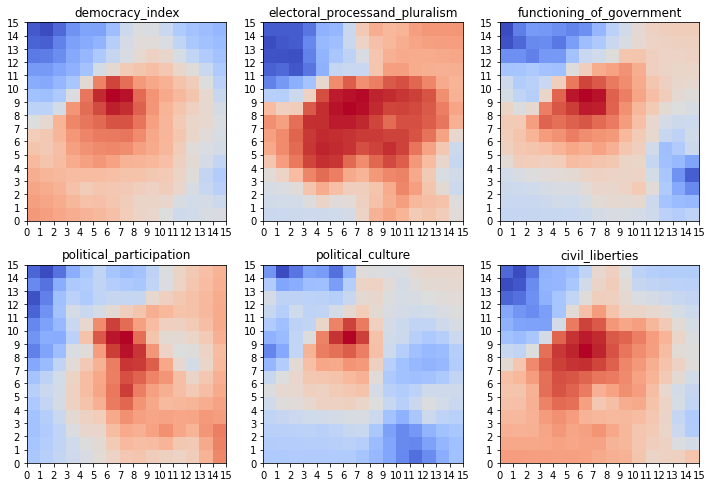
Planos de Catacterísticas#
W = som.get_weights()
plt.figure(figsize=(10, 10))
for i, f in enumerate(feature_names):
plt.subplot(3, 3, i+1)
plt.title(f)
plt.pcolor(W[:,:,i].T, cmap='coolwarm')
plt.xticks(np.arange(size+1))
plt.yticks(np.arange(size+1))
plt.tight_layout()
plt.show()
W.shape
(15, 15, 6)
W
array([[[ 8.64374915e-01, -4.50169698e-01, -3.02682978e-01,
-6.02310996e-01, -4.46642778e-01, 6.29517283e-01],
[ 8.05202458e-01, -3.92854281e-01, -2.66694796e-01,
-6.43057497e-01, -3.86914389e-01, 5.44843816e-01],
[ 7.44278989e-01, -3.31133203e-01, -2.27724788e-01,
-6.81521083e-01, -3.23807909e-01, 4.59388921e-01],
...,
[-1.46890342e+00, -1.59535361e+00, -1.20381277e+00,
-1.75580761e+00, 1.02555483e-01, -1.62261127e+00],
[-1.65153811e+00, -1.64408844e+00, -1.72309901e+00,
-1.28627034e+00, -4.30388961e-01, -1.81893501e+00],
[-1.74717853e+00, -1.54529548e+00, -1.76787926e+00,
-1.58593808e+00, -1.24030803e+00, -1.59126763e+00]],
[[ 7.99954026e-01, -4.42892025e-01, -2.95266549e-01,
-4.75381820e-01, -4.42364076e-01, 6.24196459e-01],
[ 7.40503442e-01, -3.84454044e-01, -2.58770289e-01,
-5.15635016e-01, -3.82013522e-01, 5.39468858e-01],
[ 6.76477338e-01, -3.06960506e-01, -2.11724747e-01,
-5.47200622e-01, -3.09385079e-01, 4.53850602e-01],
...,
[-1.44018686e+00, -1.60716669e+00, -1.20141418e+00,
-1.36950419e+00, -2.57206291e-01, -1.54145528e+00],
[-1.69195607e+00, -1.57934470e+00, -1.53438291e+00,
-1.48575211e+00, -1.03287481e+00, -1.73828499e+00],
[-1.86122570e+00, -1.54473433e+00, -1.34401107e+00,
-1.79916742e+00, -2.04028002e+00, -1.81717708e+00]],
[[ 7.35322833e-01, -4.35158538e-01, -2.87720534e-01,
-3.48201204e-01, -4.37989925e-01, 6.18919074e-01],
[ 6.72722642e-01, -3.67369522e-01, -2.48608290e-01,
-3.83102145e-01, -3.75479702e-01, 5.35789416e-01],
[ 6.02867920e-01, -2.28355757e-01, -1.84344337e-01,
-3.84033636e-01, -2.82851558e-01, 4.64107047e-01],
...,
[-1.29907400e+00, -1.61580450e+00, -1.33009055e+00,
-7.15700407e-01, -2.56591337e-01, -1.28486718e+00],
[-1.40556481e+00, -1.54124964e+00, -1.25623968e+00,
-9.34592999e-01, -9.31201990e-01, -1.32237951e+00],
[-1.61310457e+00, -1.54528881e+00, -1.10076567e+00,
-1.49349113e+00, -1.60718421e+00, -1.50627048e+00]],
...,
[[-2.10309783e-01, 7.42831290e-02, -4.18929818e-01,
2.72239818e-01, -1.34861411e+00, 7.13932158e-02],
[-1.95747148e-01, 1.41121606e-01, -6.41590159e-01,
3.41074688e-01, -1.09638072e+00, 5.58684217e-02],
[-1.29155995e-01, 7.39983256e-02, -5.42387688e-01,
5.92562650e-01, -8.31018729e-01, 1.43577640e-02],
...,
[-3.79730464e-01, 2.91691490e-01, 2.17007556e-01,
4.39058980e-01, 2.27946177e-01, -3.34141701e-01],
[-6.35937915e-01, 3.71465896e-01, 2.51871868e-01,
3.88900257e-01, 3.61463754e-01, -5.15397092e-01],
[-7.29862938e-01, 4.33666026e-01, 2.86797306e-01,
3.46392114e-01, 4.35014939e-01, -6.17021945e-01]],
[[-1.36536072e-01, 1.02609880e-03, -4.77226460e-01,
6.09394816e-01, -9.23636264e-01, 8.79548994e-02],
[-1.92625524e-01, 9.38826564e-02, -7.39894288e-01,
7.10439201e-01, -7.96745461e-01, -1.99956017e-01],
[-3.26542073e-01, -1.97859533e-01, -9.54418193e-01,
8.82588116e-01, -6.19115352e-01, -3.74700407e-01],
...,
[-5.88549713e-01, 3.14495906e-01, 2.16400082e-01,
5.46118593e-01, 2.88678302e-01, -4.13000332e-01],
[-7.30661544e-01, 3.83722329e-01, 2.58439096e-01,
5.15659227e-01, 3.78694054e-01, -5.34437054e-01],
[-7.99473045e-01, 4.42813270e-01, 2.95235964e-01,
4.75373824e-01, 4.42171614e-01, -6.23948977e-01]],
[[-1.11178445e-01, -2.28572486e-01, -3.66484195e-01,
9.92553665e-01, -6.17339337e-01, 2.56656858e-01],
[-2.89645176e-01, -2.48068563e-01, -7.65550425e-01,
1.03508315e+00, -6.48700844e-01, -2.78123395e-01],
[-4.87879119e-01, -4.32828184e-01, -1.25858060e+00,
1.06259458e+00, -5.43419506e-01, -6.19705296e-01],
...,
[-7.25402189e-01, 3.32354930e-01, 2.27637824e-01,
6.78660556e-01, 3.20017640e-01, -4.51947559e-01],
[-8.03294631e-01, 3.92628210e-01, 2.66429351e-01,
6.42783587e-01, 3.86294709e-01, -5.43984673e-01],
[-8.64296348e-01, 4.50152482e-01, 3.02662340e-01,
6.02302524e-01, 4.46611655e-01, -6.29479168e-01]]])
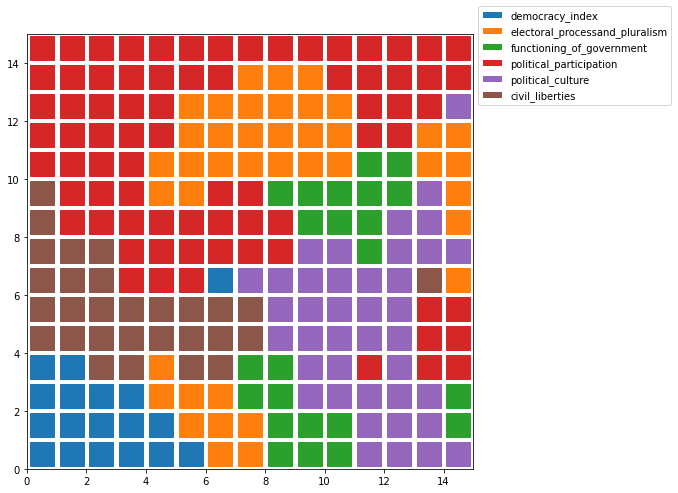
Plano de características más importantes#
Z = np.zeros((size, size))
plt.figure(figsize=(8, 8))
for i in np.arange(som._weights.shape[0]):
for j in np.arange(som._weights.shape[1]):
feature = np.argmax(W[i, j , :])
plt.plot([j+.5], [i+.5], 'o', color='C'+str(feature),
marker='s', markersize=24)
legend_elements = [Patch(facecolor='C'+str(i),
edgecolor='w',
label=f) for i, f in enumerate(feature_names)]
plt.legend(handles=legend_elements,
loc='center left',
bbox_to_anchor=(1, .95))
plt.xlim([0, size])
plt.ylim([0, size])
plt.show()
C:\Users\User\AppData\Local\Temp\ipykernel_15760\727562299.py:6: UserWarning: marker is redundantly defined by the 'marker' keyword argument and the fmt string "o" (-> marker='o'). The keyword argument will take precedence.
plt.plot([j+.5], [i+.5], 'o', color='C'+str(feature),
Referencias#
Teuvo Kohonen, Self-Organizing Maps, Third edition, Springer, 2000.
Erkki Oja and Samuel Kaski editors, Kohonen Maps, Elsevier,
Christopher Bishop, Pattern Recognition and Machine learning, Springer, 2006.


