Teoría de la Información
Contents
Teoría de la Información#
Conceptos básicos

Fuente: pixabay
Contenido o cantidad de Información#
La idea básica de la teoría de la información es que el valor de la noticia de un mensaje comunicado depende del grado en que el contenido del mensaje sea sorprendente.
Si un evento es muy probable, no es sorprendente (y generalmente poco interesante) cuando ese evento ocurre como se esperaba. Sin embargo, si es improbable que ocurra un evento, es mucho más informativo saber que el evento ocurrió o sucederá.
En teoría de la información, el contenido de información, auto-información o la sorpresa de una variable o una señal aleatoria es la cantidad de información obtenida cuando se muestrea la correspondiente distribución.
Formalmente, el contenido de información es una variable aleatoria definida para cualquier evento en la teoría de probabilidad, independientemente de si una variable aleatoria se está midiendo o no.
El contenido de la información se expresa en una unidad de información, como se explica a continuación. El valor esperado de la auto-información es la entropía teórica de la información, la cantidad promedio de información que un observador esperaría obtener sobre un sistema al muestrear la variable aleatoria.
Ejemplo para dummies#
Supongamos que se tiene una moneda sesgada, de tal manera que la probabilidad que caiga es 0.9. En símbolos de la probabilidad escribimos \(P(x_c) = 0.9\). Se lanzamos la moneda y el resultado es cara \(x=x_c\), es menos sorprendente en relación con que salga sello (cruz) \(x=x_s\). Los resultados más improbables son más sorprendentes y decimos que entregan más información sobre el experimento realizado.
Enfoque matemático#
Supongamos que \( X \) es una variable aleatoria discreta con valores \( \Omega = \{x_1, x_2, \cdots \} \) y probabilidades \( \mathcal {P} = \{p_i = P (X = x_i), \quad i = 1, 2, \cdots \} \). Si \( x \in \Omega \), el contenido de información (o información de Shannon) del conjunto (evento) \( \{x\} \) viene dado por:
Donde \(k\) es una base que depende principalmente de la cardinalidad de \( \Omega \). Si \(k=2\), la unidad de medida utilizada fue denominada bit. Si se utilizan logaritmos Neperianos, la unidad se denominan nat.
En el ejemplo para dummies, si se tiene una moneda justa, entonces \(I\{x_c\}= -\log_2 0.5 = 1\) bit. Por otro lado, si la moneda es segada como en el ejemplo, entonces \(P\{ x_c\} = -\log_2 0.9 = 0.15\) bits, mientras que \(P\{ x_s\} = -\log_2 0.1 = 3.32\) bits
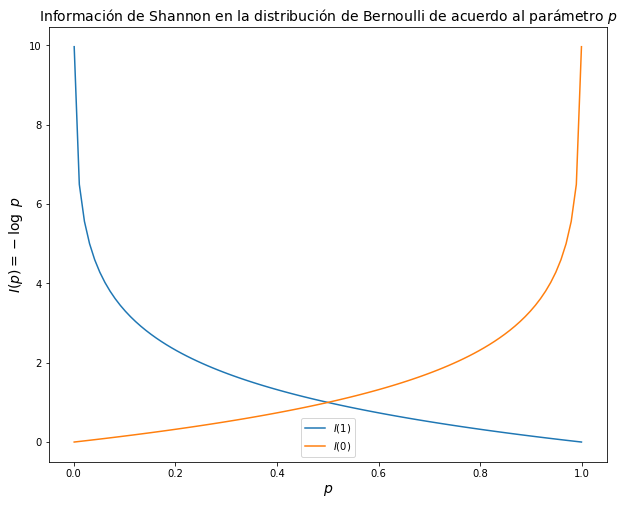
Ejemplo Distribución de Bernoulli#
Supongamos que \( X \sim Bernoulli(p)\), por lo tanto: \( x \in \{0,1 \} \). Podemos observar el comportamiento de la sorpresa al variar el parámetro de distribución de la siguiente manera:
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
fig=plt.figure(figsize=(10, 8))
plt.title('Información de Shannon en la distribución de Bernoulli de acuerdo al parámetro $p$',fontsize=14)
p=np.linspace(1e-3,1-1e-3,100)
I_1=-np.log2(p)
I_0=-np.log2(1-p)
plt.plot(p,I_1,label=r"$I(1)$")
plt.plot(p,I_0,label=r"$I(0)$")
plt.xlabel("$p$", fontsize = 14)
plt.ylabel("$I(p) = -\log \ p$", fontsize = 14)
plt.legend()
plt.show()
Entropía#
Aunque el contenido de información proporciona información interesante sobre eventos específicos \( x \), en algunos casos nos gustaría conocer el contenido de información de una distribución de probabilidad. En este asunto, lo más razonable sería estimar la información esperada. Esta estimación se conoce como entropía.
Entropía de Shannon#
Supongamos que \(X\) es una variable aleatoria discreta. Le entropía (de Shannon) de la variable aleatoria \(X\), o lo que es lo mismo, la entropía de la distribución asociada a \(X\) se define por:
Notas#
En ocasiones, la entropía de Shannon para una variable aleatoria \( X \) con probabilidades \( p_1, \ldots, p_M \) se denota \( H (p_1, \ldots, p_M) \). Por ejemplo, la entropía de una distribución de Bernoulli a veces se denota \(H(p,q)= H(p,1-p)\).
Algunos autores llaman a \(H(X)\) como incertidumbre.
\(H(X)\) Es una esperanza. La entropía es solo la sorpresa media de la variable aleatoria \(H(X)\).
Racional #
Para comprender el significado de \( - \sum_i p_i \log p_i \), primero defina una función de información \( I \) en términos de un evento \( i \) con probabilidad \( p_i \). La cantidad de información adquirida debido a la observación del evento \( i \) se deduce de la solución de Shannon de las propiedades fundamentales de la información:
\(I(p)\) disminuye monotónicamente en \( p \): un aumento en la probabilidad de un evento disminuye la información de un evento observado, y viceversa.
\(I(p)\ge 0\) : la información es una cantidad no negativa.
\(I(1) = 0\) : los eventos que siempre ocurren no comunican información.
\(I(p_1 p_2) = I(p_1) + I(p_2)\) : La información debida a eventos independientes es aditiva.
La última es una propiedad crucial. Establece que la probabilidad conjunta de fuentes de información independientes comunica tanta información como los dos eventos individuales por separado.
\(\leadsto\) La entropía proporciona una medida sobre la información promedio de una distribución. Por ejemplo, en el caso de Bernoulli, la entropía máxima se logra cuando el parámetro es 0.5, es decir, cuando todos los eventos son igualmente probables.
Hay una interpretación importante de la entropía que está relacionada con el número promedio de «contenedores» o shannons (relacionados con la base del logaritmo, en este caso 2) necesarios para representar la información de \( X \). En el caso de Bernoulli, requerimos 1 bit para representar los datos.
Dos desigualdades de la Teoría de la Información#
Se puede comprobar que si \(0\le p \le 1\), entonces \(-p\log p\ge 0\).
-\(\leadsto\) Esto implica que la entropía de Shannon es siempre positiva.
Adicionalmente, si \(p_1,\ldots,p_M\) y \(q_1,\ldots,q_M\) números positivos arbitrarios tales que \(\sum_i p_1 =1\), y \(\sum_i q_i=1\). Entonces,
la igualdad se tiene si y solo si \(p_i=q_i\) para todo \(i\)*.
Teorema#
la igualdad se tiene si y solo si para todo \(p_i\), se tiene que \(p_i = 1/M\).
Este teorema nos ayuda a entender la entropía de la siguiente manera.
Entre las distribuciones discretas con \( M \) posibles resultados, la distribución uniforme \( U \{x_1, \ldots, x_m \} \) tiene la mayor entropía. Esto se debe a que los resultados de la variable tienen la misma información que contienen (sorpresa).
En general, la entropía es mayor para variables aleatorias discretas con mayor número de valores posibles. En particular, la entropía de la distribución uniforme (\( \log M \)) es una función creciente de \( M \).
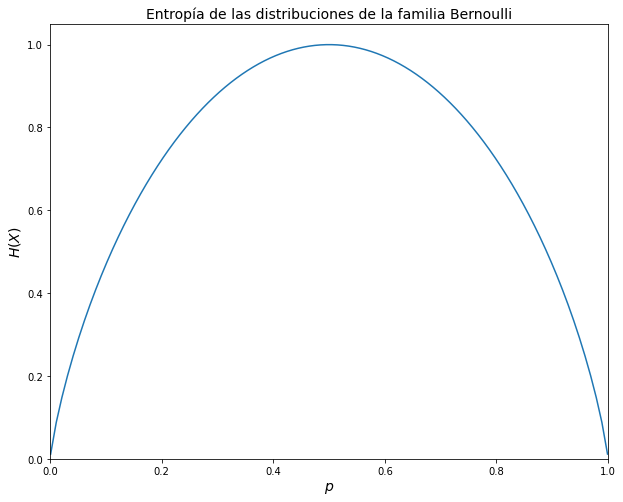
Ejemplo: Entropía de las distribuciones de la familia Bernoulli#
Supongamos que \(X\sim Bernoulli(p)\), por lo tanto: \(x \in \{0,1\}\), Podemos observar el comportamiento de la entropía al variar el parámetro de distribución en la siguiente gráfica
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
fig=plt.figure(figsize=(10,8))
H_ber=lambda X: -np.sum(X*np.log2(X),axis=1) #Función para estimar la entropía de la distribución Bernoulli
p=np.linspace(1e-3,1-1e-3,100)
probs_X=np.vstack([p,1-p]).T
plt.plot(p,H_ber(probs_X))
plt.xlabel("$p$",fontsize =14)
plt.ylabel("$H(X)$",fontsize =14)
plt.ylim([0,1.05])
plt.xlim([0,1])
plt.title('Entropía de las distribuciones de la familia Bernoulli',fontsize =14)
plt.show()
Entropía Conjunta#
Sean \(X\) y \(Y\) variables aleatorias discretas que tienen una función de probabilidad conjunta:
Es natural definir la entropía conjunta de \( X \) y \( Y \) como:
Se puede verificar que:
la igualdad se tiene si y solo si \(X\) y \(Y\) son independientes.
Entropía Condicional#
Supongamos que \( X \) y \( Y \) sean variables aleatorias discretas con distribución conjunta \( p (x_i, y_j) \). Si se sabe que \( X = x_i \), la distribución de \( Y \) se caracteriza por el conjunto de probabilidades condicionales \( p (y_j | x_i) \). Por lo tanto definimos la entropía condicional de \( Y \) dado \( X = x_i \) como:
La entropía condicional de \( Y \) dado \( X \) es el promedio ponderado promedio de \( H (Y | X = x_i) \), es decir:
Se puede verificar que:
y
La igualdad se tiene si y solo si \(X\) y \(Y\) son independientes.
Información mutua#
Suponga que \( X \) y \( Y \) son variables aleatorias discretas con funciones de masa de probabilidad dadas por \( f_X \) y \( f_Y \) respectivamente, y una función de masa de probabilidad conjunta \( f \). Así, la información mutua de \( X \) y \( Y \), denotada \( \mathfrak {M} (X, y) \) se define como:
Notas#
La dependencia mutua es una medida de dependencia entre las variables \( X \) y \( Y \). Tenga en cuenta que si \( X \) y \( Y \) son independientes, su información mutua es cero.
Si \( X \) y \( Y \) tienen exactamente la misma distribución, entonces \(\mathfrak{M}(X,Y) = H(X)\).
La divergencia Kullback-Leibler#
La divergencia de Kullback-Leibler (KL) es una pseudo-distancia que representa la diferencia entre dos distribuciones. Debido a su definición, también se conoce como entropía relativa, porque es el valor esperado de un contenido de información de la relación entre dos distribuciones. Se define la divergencia KL como:
Caso discreto:
\(\Omega\) es el soporte de las distribuciones.
Observe que si \(P=Q\) c.s., entonces \(KL(P||Q)=0.\)
Entropía cruzada#
Suponga que \(f\) y \(g\) son dos funciones de de probabilidad (o masa de probabilidad). La entropía cruzada entre \(f\) y \(g\) se define como:
Se puede comprobar que:
Llamamos \( f \) como la distribución de referencia y \( g \) como la distribución aproximada.
\(\leadsto\) Tenga en cuenta que la divergencia KL y la entropía cruzada difieren en \( H (f) \), la entropía de la distribución de referencia. Por otro lado, \( H (f) \) que es constante con respecto a \( g \). Por esta razón, algunos autores llaman KL-divergencia como entropía cruzada.
Entropía cruzada como función de pérdida#
En el aprendizaje automático, es común utilizar la entropía cruzada como criterio para evaluar la convergencia de un proceso de aprendizaje (comúnmente un proceso de optimización).
Supongamos que en un problema de clasificación tenemos T clases. Ahora suponga que cada uno de los objetos de entrenamiento \( x_i \) pertenece a una clase única, digamos \( C_{it} \). Por lo tanto, una forma común de representar la clase del vector \( x_i \) es mediante el uso de un vector T, que tiene todos los elementos iguales a cero, excepto la posición ti, que tiene 1.
En estadística, esta codificación se denomina codificación dummy. En el lenguaje de aprendizaje automático se llama hot one encoding.
La cuestión clave es que esta codificación representa una distribución del vector de entrenamiento de entrada. Esta es la distribución de referencia para la entrada.
Por otro lado, en cada época (iteración) del entrenamiento de la máquina, la salida es una distribución de propuesta \( s_i \) del vector de entrada. Esta es la distribución aproximada del vector de entrada. Por lo tanto, la entropía cruzada en este caso viene dada por:
Si tenemos \( N \) vectores de entrenamiento, la codificación dummy completa es una matriz \( N \) \( \times \) \( T \), digamos \( L \), donde cada celda \( it \) se define como \( l_ {it} = 1 \) es la entrada de entrenamiento \( x_ {i} \) pertenece a la clase \(t\), y \( 0 \) de lo contrario.
La función de pérdida de entropía cruzada se debe minimizar en el proceso de entrenamiento es dada:
\(\leadsto\) Por ejemplo en una red neuronal, \(s_i =(s_{i1}, \ldots, s_{iT})\) es la capa de salida, y es producida por la función softmax.
Máxima verosimilitud y función de pérdida#
Suponga que cada uno de los vectores de entrenamiento de entrada tiene una función de densidad de probabilidad dada por \( f (x_i, w), i = 1, \ldots, N \), donde \( w \) es el parámetro a aprender. También suponga que los \( x_i \) son independientes.
En la estimación de máxima verosimilitud \( l(w | x) = - \sum_i \log f(x_i; w) \) es la función de pérdida que debe minimizarse.
Por ejemplo la función de pérdida torch.nn.GaussianNLLLoss en Pytorch es la función de pérdida basada en el supuesto que cada observación es de tipo Gaussiano. Técnicamente tal función de pérdida se define por:
En este caso, \(net(x_i)\) es la predicción de la red neuronal y \(y_i\) la variable target correspondiente. Adicionalmente \(\epsilon>0\) se introduce para evitar problemas convergencia con valores muy pequeños de \(\sigma^2\).
El siguiente fragmento de código muestra cómo usar esta función de pérdida.
import torch
from torch import nn
loss = nn.GaussianNLLLoss()
input = torch.randn(5, 2, requires_grad=True)
target = torch.randn(5, 2)
var = torch.ones(5, 2, requires_grad=True) #heterocedasticidad
output = loss(input, target, var)
output.backward()
Un ejemplo simple de aplicación con redes neuronales #
El siguiente código muestra la implementación de un red neuronal simple de dos capas que se usará para el entrenamiento de un clasificador dicotómico. Revise la función de pérdida definida. en este ejemplo simple, el número de datos de entrenamiento es muy pequeño y fijo, por lo que no es necesario el factor \(1/N\). Observe que la función de pérdida es exactamente menos la log verosimilitud de un modelo de Bernoulli.
# define la activación de salida
import numpy as np
def sigmoid(x):
return 1.0/(1+np.exp(-x))
# define la red neuronal
def net(params, x):
w1, b1, w2, b2 = params
hidden = np.tanh(np.dot(w1,x) + b1)
return (sigmoid(np.dot(w2,hidden) + b2))
# función de pérdida de la entropía cruzada
def loss(params, x,y):
out = net(params,x)
cross_entropy = -y * np.log(out) - (1-y)*np.log(1-out) # esto es -log verosimilitud
return cross_entropy


