Ejemplos de Modelos
Contents
Ejemplos de Modelos#
Introducción#
Ahora que hemos visto el gran potencial de lo que significa modelar, ejemplifiquemos diferentes modelos que han aparecido a lo largo de la historia.
1. Modelos Mentales#
El primer modelo matemático existente podría considerarse como la abstracción de los números para aprender a contar:
:max_bytes(150000):strip_icc():format(webp)/U21C6.svg-5c5c5c52c9e77c0001d92a41.png)
Fuente: lifewire
Fuente: Wikipedia
En este modelo, la idea era poder representar los objetos de la vida cotidiana como símbolos (en lo posible fáciles de manipular) para poder aumentar nuestra capacidad de cálculo y por lo tanto el poder de predecir.
Muchos siglos después, se desarrollaría un modelo basado en modelos matemáticos: Física.
El objetivo de la física sería usar estos modelos matemáticos ya desarrollados para poder predecir cosas útiles sobre el mundo real.
Por ejemplo, anteriormente, cuando ocurrían eclipses solares, lunares o pasaba algún cometa cerca de la tierra, muchas culturas lo consideraban como un castigo de los dioses, pues no tenían un entendimiento suficiente sobre lo que estaba ocurriendo; en otras palabras era un acontecimiento sobrenatural.
2. Modelos Determinísticos#
Historia#
La primera persona en tratar de romper estos mitos (uno de ellos, muy aclamado en el momento, era que todo el cosmos giraba alrededor de la tierra) fue el personaje a continuación:

Fuente: Wikipedia
Ecuaciones de Movimiento (Cinemática)#
Comencemos a pensar sobre el mundo real.
¿Qué podemos decir sobre los objetos que caen?
¿Existe alguna fuerza invisible que los atrae contra el suelo cómo si de hilos mágicos se tratase?
Cuidado
¿Qué cae más rápido al suelo?

Fuente: Steemitimages
Respuesta
Puedes dar clic aquí para ver la respuesta.
Asumamos entonces que aquella fuerza invisible que atrae los objetos al suelo es una constante y llamémosla \(g\).
Ahora, analicemos lo siguiente de la naturaleza:
Percibimos el movimiento de los objetos.
Sabemos medir distancias (Gracias a los números).
Percibimos el tiempo.
Podemos percibir y medir el cambio de la distancia a través del tiempo (Velocidad).
Podemos percibir y medir el cambio de la velocidad en el tiempo (Aceleración).
De cálculo básico sabemos que:
Recordemos que \(a=\frac{dv}{dt}\). Entonces, integrando obtenemos:
Consejo para la vida: La cosas siempre tienen una condición inicial. Por ejemplo,
Por lo tanto,
Usando un proceso similar (Tarea), llegamos a que:
Combinando las anteriores ecuaciones tenemos el siguiente conjunto total (Tarea):
\(v(t)=v_o-gt\)
\(x(t) = x_o+v_o t -\frac{1}{2}gt^2 \)
\(v^2(t) = v_{o}^2 -2g(x(t)-x_o)\)
Estas ecuaciones fueron las primeras ecuaciones que pretendían predecir los movimientos de los objetos, y fueron aquellas usadas por Galileo Galilei para pensar sobre la trayectoria de los objetos.
Gracias a este pensamiento, fue posible salir de la oscuridad y concluir que sólo somos un pálido punto girando alrededor de otro pequeño punto dentro de un vasto cosmos.
Leyes de Newton#
Otro caso de éxito, fueron las famosas ecuaciones de Isaac Newton. Tan poderosas que con ellas fuimos capaces de ir a la Luna y volver con vida.
Tal vez, la más importante es la segunda:
Volviendo a escribir dicha ecuación en términos de ecuaciones diferenciales, tenemos:
O sea, despejando, tenemos:
En los cursos de física básica, muchas veces las fuerzas son constantes, pero en general, las fuerzas pueden cambiar en el tiempo.
En otras palabras, tenemos la siguiente ecuación diferencial:
Que quiere decir que la Fuerza ejercida en un objeto puede depender tanto del tiempo como de la posición y de la velocidad.
El objetivo general del modelamiento es poder escribir dicha ecuación (es decir, describir la forma que tiene la fuerza) y resolver la ecuación resultante.
Modelos Lineales#
No todos los modelos son ecuaciones diferenciales. A veces, es posible modelar problemas que no cambian en el tiempo cuando las condiciones de un problema no cambian en el tiempo.
Todos estos problemas se pueden modelar como:
es decir, como un sistema de ecuaciones lineales.
Estamos entonces en el ámbito del Álgebra Lineal.
Ejemplo#
Supongamos que en una empresa se fabrican 100 productos y trabajan 100 empleados diferentes.
Si pudieramos registrar cuantas horas se demora cada uno de los empleados en fabricar cada uno de los productos, fijando ciertas horas de trabajo laboral en un contrato, podríamos resumir la información en la siguiente tabla:
Emp\Prod |
\( x_1 \) |
\( x_2 \) |
\(\dots\) |
\(x_{100}\) |
|---|---|---|---|---|
\(E_1\) |
3 |
4 |
\(\dots\) |
7 |
\(E_2\) |
2 |
5 |
\(\dots\) |
8 |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(E_{100}\) |
1 |
8 |
\(\dots\) |
2 |
O sea, podemos generar la siguiente matriz:
Si fijamos las horas totales de trabajo por empleado y llamamos a dichas horas el vector \(\vec{b}\), podemos construir el siguiente modelo:
Entonces, si queremos saber cuántos productos son capaces de producir los empleados de cada producto, debemos solucionar dicho sistema de ecuaciones.
Recuerde
Un sistema tiene sólo tres opciones:
Tiene solución:
Solución Única.
Infinitas Soluciones.
No tiene solución (inconsistente).
Supongamos que tiene solución única. La solución se escribe como:
Ejercicio 1#
Realice un código que haga lo siguiente:
Genere una matriz de números aleatorios enteros \(100\times100\) y un vector de números aleatorios para solucionar el problema anterior.
Interprete las soluciones.
Generalice el problema a matrices rectangulares.
¿Qué ocurre si un sistema no tiene solución?
¿Y si tiene infinitas soluciones?
Ecuaciones Diferenciales Parciales#

Fuente: Wikipedia
Ecuaciones de Maxwell (En el vacío):
3. Modelos Estocásticos#
Modelos Estadísticos:#
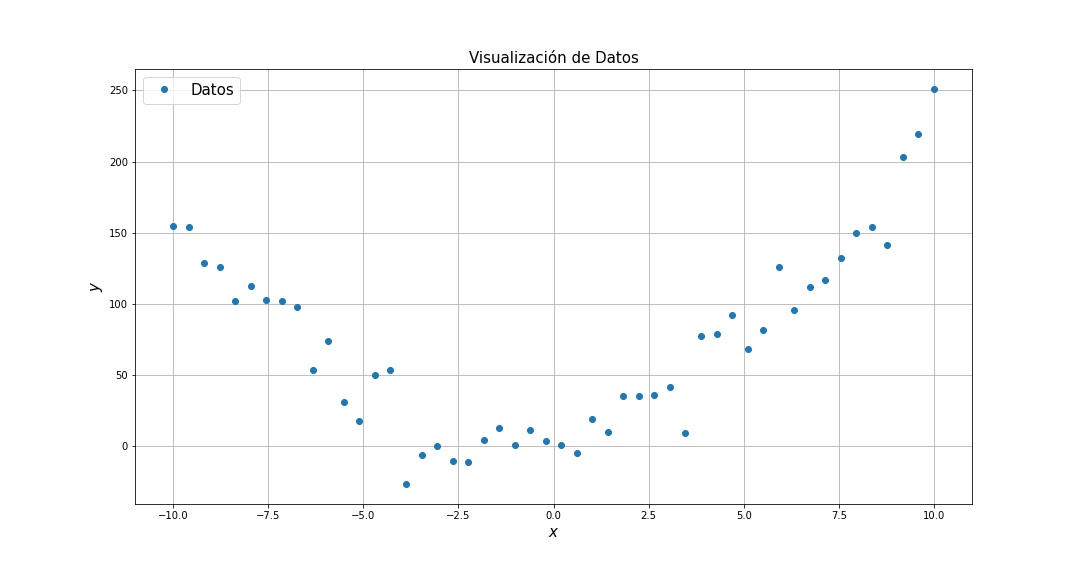
Regresión Inocente:
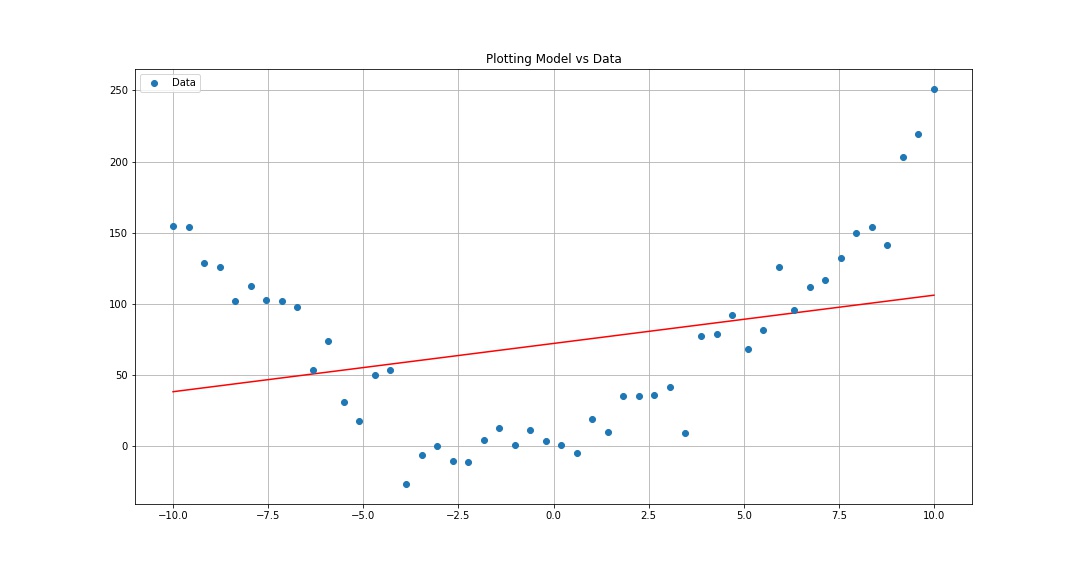
Regresión usando una Red Neuronal:
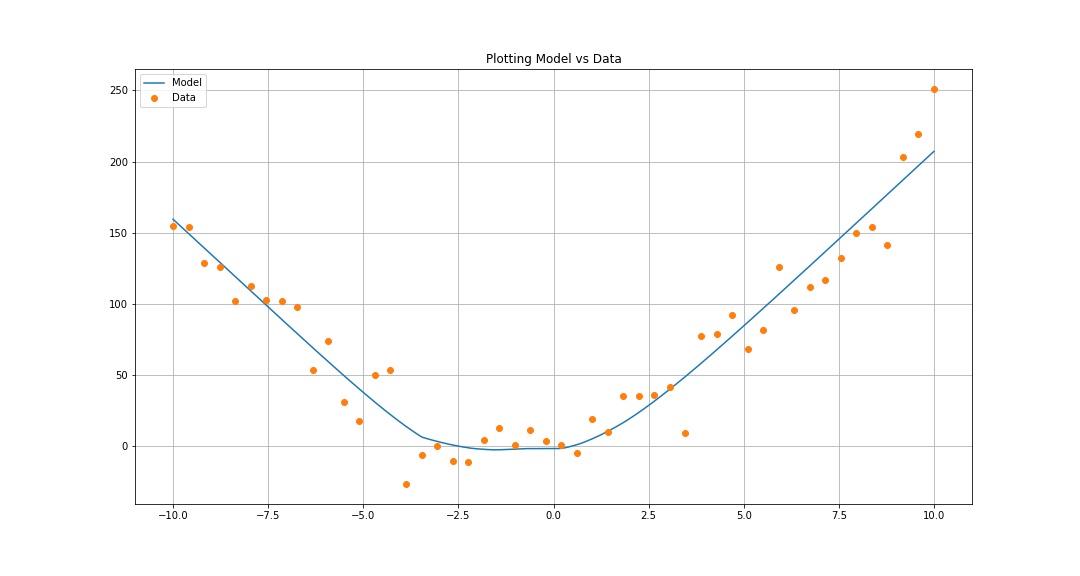
Criterio de Evaluación
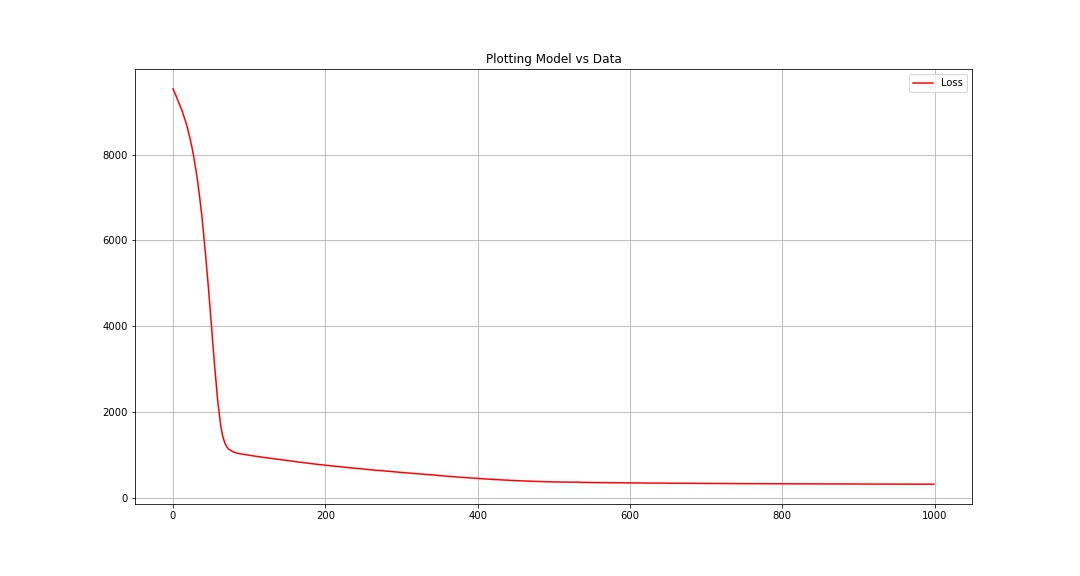
Teorema de Aproximación Universal#
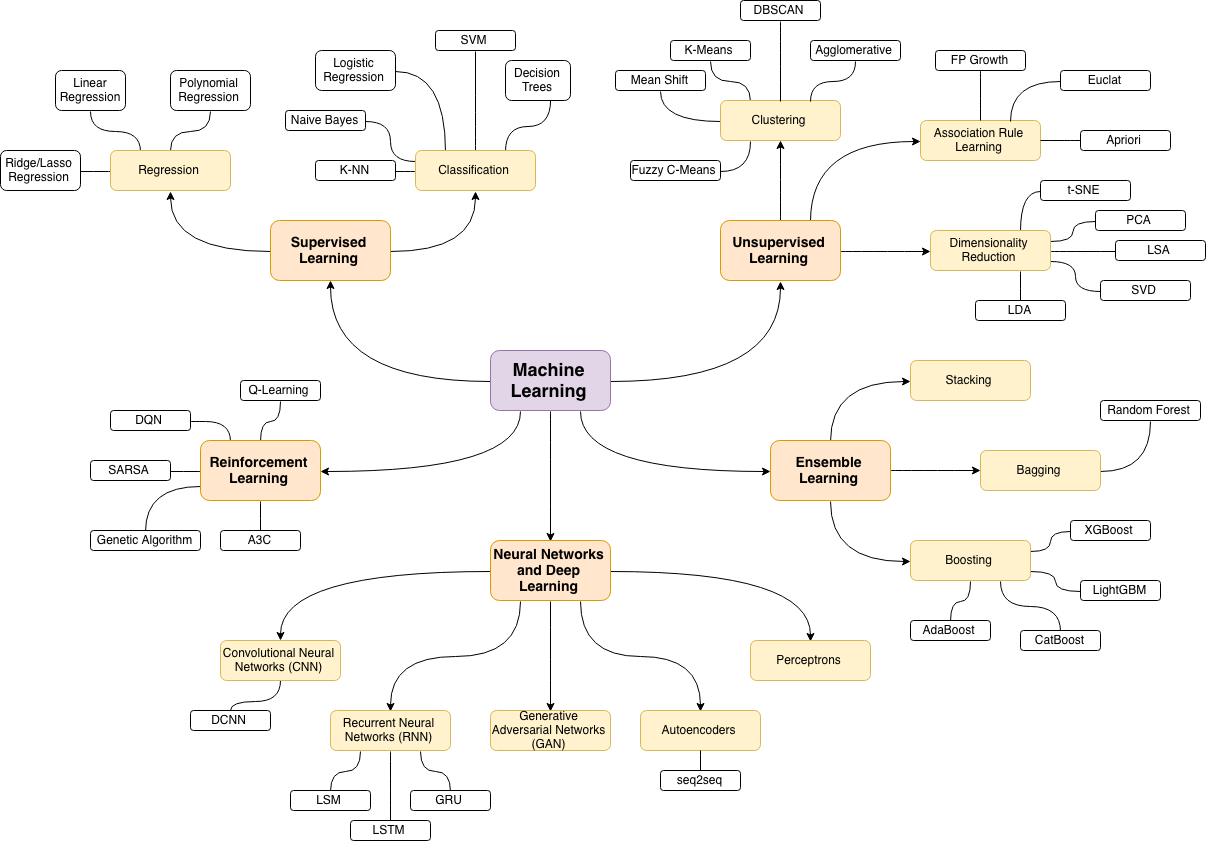
Fuente: Homemade Machine Learning


