Regresion Basica con tf.keras: Predecir eficiencia de la gasolina
Contents
Regresion Basica con tf.keras: Predecir eficiencia de la gasolina#
Introducción#
Información general sobre Tensorflow.
 Vea el cuaderno original en: TensorFlow.org
Vea el cuaderno original en: TensorFlow.org
En un problema de regresión, buscamos predecir la salida de un valor continuo como la probabilidad de un precio. En contraste en un problema de Clasificación, buscamos seleccionar una clase de una lista de clases (por ejemplo, en donde una imagen contenga una manzana o una naranja queremos reconocer cual es la fruta en la imagen).
En este cuaderno se usa el set de datos clásico Auto MPG y se construye un modelo para predecir la eficiencia de vehículos de 1970 y 1980. Para hacer esto proveeremos el modelo con una descripción de muchos automóviles de ese periodo. Esta descripción incluye atributos como: Cilindros, desplazamiento, potencia y peso.
Este ejemplo usa el API Sequential de tf.keras.
Importa librerías requeridas#
from __future__ import absolute_import, division, print_function
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.utils import plot_model
import pathlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
print(tf.__version__)
2.9.1
El conjunto de Datos de MPG#
El set de datos esta disponible de el siguiente repositorio UCI Machine Learning Repository.
Lectura de los datos#
Primero descargue el set de datos.
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
'C:\\Users\\User\\.keras\\datasets\\auto-mpg.data'
Importelo usando pandas.
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
| MPG | Cylinders | Displacement | Horsepower | Weight | Acceleration | Model Year | Origin | |
|---|---|---|---|---|---|---|---|---|
| 393 | 27.0 | 4 | 140.0 | 86.0 | 2790.0 | 15.6 | 82 | 1 |
| 394 | 44.0 | 4 | 97.0 | 52.0 | 2130.0 | 24.6 | 82 | 2 |
| 395 | 32.0 | 4 | 135.0 | 84.0 | 2295.0 | 11.6 | 82 | 1 |
| 396 | 28.0 | 4 | 120.0 | 79.0 | 2625.0 | 18.6 | 82 | 1 |
| 397 | 31.0 | 4 | 119.0 | 82.0 | 2720.0 | 19.4 | 82 | 1 |
Preprocesamiento#
Detecta datos faltantes y elimina filas#
El set de datos contiene algunos valores desconocidos.
dataset.isna().sum()
MPG 0
Cylinders 0
Displacement 0
Horsepower 6
Weight 0
Acceleration 0
Model Year 0
Origin 0
dtype: int64
Para Mantener este tutorial inicial sencillo eliminemos las siguientes filas.
dataset = dataset.dropna()
Codificación one-hot#
La columna de "Origin" realmente es categórica, no numérica. Entonces conviértala a un «one-hot»:
# retira 'Origin' de dataset y lo entrega. Se recibe en la variable origin
Origin = dataset.pop('Origin')
dataset['USA'] = (Origin == 1)*1.0
dataset['Europe'] = (Origin == 2)*1.0
dataset['Japan'] = (Origin == 3)*1.0
dataset.tail()
| MPG | Cylinders | Displacement | Horsepower | Weight | Acceleration | Model Year | USA | Europe | Japan | |
|---|---|---|---|---|---|---|---|---|---|---|
| 393 | 27.0 | 4 | 140.0 | 86.0 | 2790.0 | 15.6 | 82 | 1.0 | 0.0 | 0.0 |
| 394 | 44.0 | 4 | 97.0 | 52.0 | 2130.0 | 24.6 | 82 | 0.0 | 1.0 | 0.0 |
| 395 | 32.0 | 4 | 135.0 | 84.0 | 2295.0 | 11.6 | 82 | 1.0 | 0.0 | 0.0 |
| 396 | 28.0 | 4 | 120.0 | 79.0 | 2625.0 | 18.6 | 82 | 1.0 | 0.0 | 0.0 |
| 397 | 31.0 | 4 | 119.0 | 82.0 | 2720.0 | 19.4 | 82 | 1.0 | 0.0 | 0.0 |
Ejercicio#
Investigue como hacer esta codificación one-hot utilizando
tf.keras.utils.to_categorical
Dividir los datos en entrenamiento y test#
Ahora divida el set de datos en un set de entrenamiento y otro de pruebas.
Usaremos el set de pruebas en la evaluación final de nuestro modelo.
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
train_dataset.keys()
Index(['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'USA', 'Europe', 'Japan'],
dtype='object')
Descriptivo de los datos#
Revise rápidamente la distribución conjunta de un par de columnas de el set de entrenamiento.
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
<seaborn.axisgrid.PairGrid at 0x1b6c82988e0>
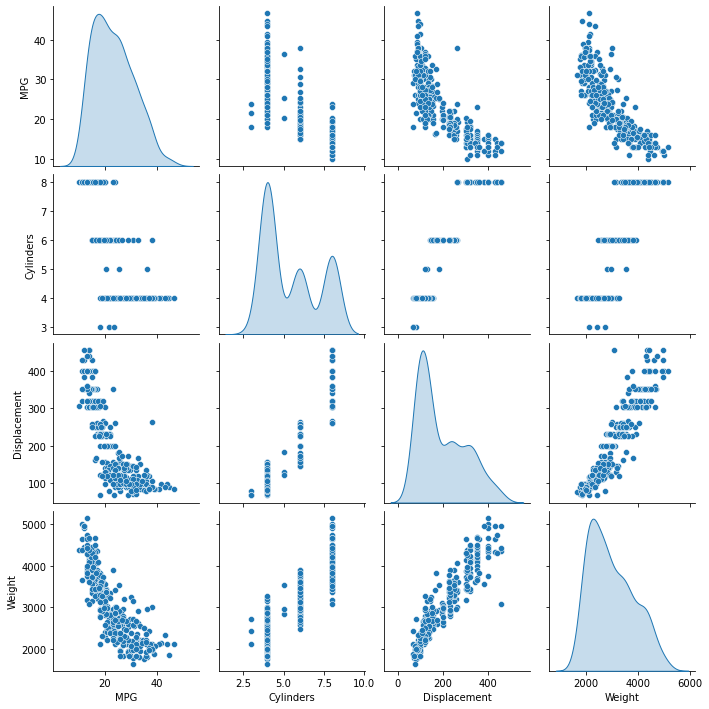
Tambien revise las estadisticas generales:
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| Cylinders | 314.0 | 5.477707 | 1.699788 | 3.0 | 4.00 | 4.0 | 8.00 | 8.0 |
| Displacement | 314.0 | 195.318471 | 104.331589 | 68.0 | 105.50 | 151.0 | 265.75 | 455.0 |
| Horsepower | 314.0 | 104.869427 | 38.096214 | 46.0 | 76.25 | 94.5 | 128.00 | 225.0 |
| Weight | 314.0 | 2990.251592 | 843.898596 | 1649.0 | 2256.50 | 2822.5 | 3608.00 | 5140.0 |
| Acceleration | 314.0 | 15.559236 | 2.789230 | 8.0 | 13.80 | 15.5 | 17.20 | 24.8 |
| Model Year | 314.0 | 75.898089 | 3.675642 | 70.0 | 73.00 | 76.0 | 79.00 | 82.0 |
| USA | 314.0 | 0.624204 | 0.485101 | 0.0 | 0.00 | 1.0 | 1.00 | 1.0 |
| Europe | 314.0 | 0.178344 | 0.383413 | 0.0 | 0.00 | 0.0 | 0.00 | 1.0 |
| Japan | 314.0 | 0.197452 | 0.398712 | 0.0 | 0.00 | 0.0 | 0.00 | 1.0 |
Separe características y etiquetas#
Separe el valor objetivo, o la «etiqueta» de las caracteristicas. Esta etiqueta es el valor que entrenara el modelo para predecir.
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
Normalice los datos#
Revise otra vez el bloque de train_stats que se presento antes y note la diferencia de rangos de cada característica.
Es una buena práctica normalizar variables que utilizan diferentes escalas y rangos. Aunque el modelo podría converger sin normalización de características, dificulta el entrenamiento y hace que el modelo resultante dependa de la elección de las unidades utilizadas en la entrada.
Nota
Aunque generamos intencionalmente estas estadísticas solo del conjunto de datos de entrenamiento, estas estadísticas también se utilizarán para normalizar el conjunto de datos de prueba. Necesitamos hacer eso para proyectar el conjunto de datos de prueba en la misma distribución en la que el modelo ha sido entrenado.
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
Estos datos normalizados es lo que usaremos para entrenar el modelo.
Precaución
Las estadísticas utilizadas para normalizar las entradas aquí (media y desviación estándar) deben aplicarse a cualquier otro dato que se alimente al modelo, junto con la codificación de un punto que hicimos anteriormente. Eso incluye el conjunto de pruebas, así como los datos en vivo cuando el modelo se usa en producción.
Construye el modelo Sequential modo 1#
Construyamos nuestro modelo. Aquí, utilizaremos un modelo secuencial con dos capas ocultas densamente conectadas y una capa de salida que devuelve un único valor continuo. Los pasos de construcción del modelo se envuelven en una función, build_model, ya que crearemos un segundo modelo, más adelante.
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=(normed_train_data.shape[1],)),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
Compila#
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
Summary#
model.summary()
plot_model(model, to_file='../Imagenes/gasolina_model.png',
show_shapes=True)
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 64) 640
dense_1 (Dense) (None, 64) 4160
dense_2 (Dense) (None, 1) 65
=================================================================
Total params: 4,865
Trainable params: 4,865
Non-trainable params: 0
_________________________________________________________________
You must install pydot (`pip install pydot`) and install graphviz (see instructions at https://graphviz.gitlab.io/download/) for plot_model/model_to_dot to work.
Entrena#
Entrene el modelo durante 1000 epochs y registre la precisión de entrenamiento y validación en el objeto history.
# Display training progress by printing a single dot for each completed epoch
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
epochs = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=epochs, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
...
...
...
...
..
...
...
...
...
...
...
...
...
...
..
...
...
...
...
...
...
...
...
..
...
..
...
..
..
..
..
..
..
...
...
..
..
.
.
..
..
..
....
....
....
..
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
.
..
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
..
.
...
...
...
...
...
...
Visualice el progreso de entrenamiento del modelo usando las estadísticas almacenadas en el objeto history.
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
| loss | mae | mse | val_loss | val_mae | val_mse | epoch | |
|---|---|---|---|---|---|---|---|
| 995 | 2.626115 | 1.045127 | 2.626115 | 8.123038 | 2.095079 | 8.123038 | 995 |
| 996 | 2.807523 | 0.997537 | 2.807523 | 8.852625 | 2.232581 | 8.852625 | 996 |
| 997 | 2.563603 | 1.008386 | 2.563603 | 8.025837 | 2.082879 | 8.025837 | 997 |
| 998 | 2.623543 | 0.978624 | 2.623543 | 8.230783 | 2.076313 | 8.230783 | 998 |
| 999 | 2.500173 | 0.982198 | 2.500173 | 8.858159 | 2.232028 | 8.858159 | 999 |
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mae'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mae'],
label = 'Val Error')
plt.ylim([0,5])
plt.legend()
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mse'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mse'],
label = 'Val Error')
plt.ylim([0,20])
plt.legend()
plt.show()
plot_history(history)
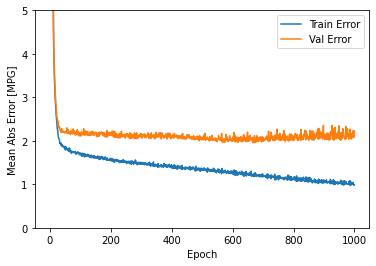
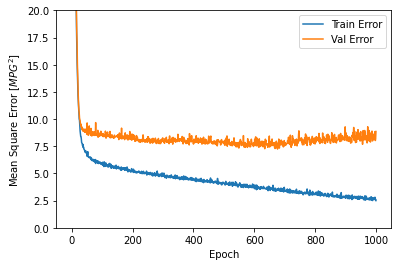
Este gráfico muestra poca mejora, o incluso degradación en el error de validación después de aproximadamente 100 épocas. Actualicemos la llamada model.fit para detener automáticamente el entrenamiento cuando el puntaje de validación no mejore. Utilizaremos una * devolución de llamada de EarlyStopping * que pruebe una condición de entrenamiento para cada época. Si transcurre una cantidad determinada de épocas sin mostrar mejoría, entonces detiene automáticamente el entrenamiento.
Puedes obtener más información sobre esta devolución de llamada Aca.
# The patience parameter is the amount of epochs to check for improvement
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=epochs,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
...............
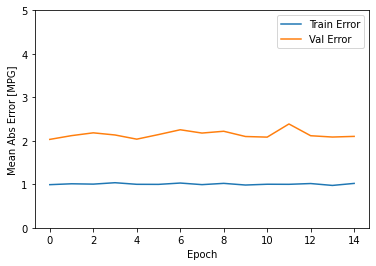
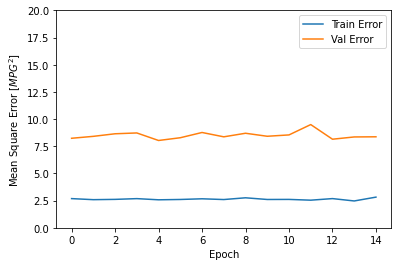
El gráfico muestra que en el conjunto de validación, el error promedio generalmente es de alrededor de +/- 2 MPG. ¿Es esto bueno? Le dejaremos esa decisión a usted.
Veamos qué tan bien generaliza el modelo al usar el conjunto ** test **, que no usamos al entrenar el modelo. Esto nos dice qué tan bien podemos esperar que el modelo prediga cuándo lo usamos en el mundo real.
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
3/3 - 0s - loss: 6.3022 - mae: 2.0424 - mse: 6.3022 - 40ms/epoch - 13ms/step
Testing set Mean Abs Error: 2.04 MPG
Predicciones#
Finalmente, prediga los valores de MPG utilizando datos en el conjunto de pruebas:
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
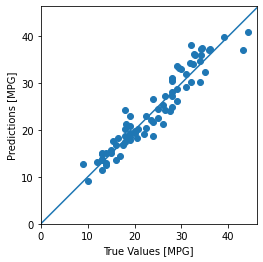
Parece que nuestro modelo predice razonablemente bien. Echemos un vistazo a la distribución de errores.
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
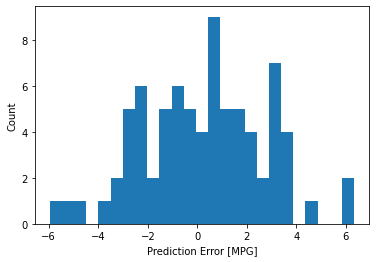
No es del todo gaussiano, pero podríamos esperar eso porque el número de muestras es muy pequeño.
Conclusión#
Este cuaderno introdujo algunas técnicas para manejar un problema de regresión.
El error cuadrático medio (MSE) es una función de pérdida común utilizada para problemas de regresión (se utilizan diferentes funciones de pérdida para problemas de clasificación).
Del mismo modo, las métricas de evaluación utilizadas para la regresión difieren de la clasificación. Una métrica de regresión común es el error absoluto medio (MAE).
Cuando las características de datos de entrada numéricos tienen valores con diferentes rangos, cada característica debe escalarse independientemente al mismo rango.
Si no hay muchos datos de entrenamiento, una técnica es preferir una red pequeña con pocas capas ocultas para evitar el sobreajuste.
La detención temprana es una técnica útil para evitar el sobreajuste.


