Conceptos básicos de aprendizaje de máquinas

Introducción

Consideremos el ejemplo de reconocimiento de dígitos escritos a mano, ilustrado en esta figura.

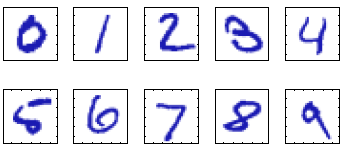
Fuente: Ejemplo de dígitos a mano alzada del conjunto MNIST

Cada dígito corresponde a una imagen de \(28\times28\) píxeles y, por lo tanto, puede representarse mediante un vector (tensor unidimensional) \(x\) que consiste de \(784\) números entre \(0\) y \(255\) (o entre \(0\) y \(1\)). El objetivo es construir una función que tome un vector \(x\) como entrada y que produzca la identidad del dígito \((0,\dots,9)\) como salida.

Máquina de aprendizaje

Para definir una función de aprendizaje es necesario tener en cuenta que desde el comienzo tenemos un espacio de entrada, digamos \(\mathcal{S}\), en el cual están los objetos para los cuales se desea hacer una asignación de un objeto que está en otro espacio de salida, que vamos a denotar \(\mathcal{R}\). La definición del espacio \(\mathcal{R}\) depende del problema.

Una máquina de aprendizaje es una función \(f\) que asocia a cada elemento de \(\mathcal{S}\) un único elemento en \(\mathcal{R}\). Escribiremos:

\[f: \mathcal{S} \to \mathcal{R}\]

Si \(x\) es un elemento del espacio \(\mathcal{S}\), escribimos \(x\in\mathcal{S} \), entonces la notación \(y = f(x)\), significa que \(y\) es el único elemento de \(\mathcal{R}\) asociado a \(x\).

En la figura anterior, si \(x\) es el tensor que representa la imagen superior izquierda, entonces es posible que definamos \(f(x) = 0\).

Es importante tener en cuenta que si el problema es asignar una etiqueta al tensor \(x\), entonces el valor \(0\) en este caso no es nada más que una etiqueta. La siguiente gráfica muestra posibles valores de la máquina de aprendizaje \(f\) en este problema.

Función: Ejemplo de algunos valores de la máquina de aprendizaje (función) \(f\)

En este ejemplo el espacio de entrada \(\mathcal{S}\) es el conjunto de todos los tensores de tamaño \(28\times 28\), cuyos valores están en el intervalo \([0,255]\). Este espacio es finito, pero muy grande: \(256^{56}\). ¿Puede imaginar este tamaño?

Adicionalmente, el conjunto de salida \(\mathcal{R}\) es el conjunto de etiquetas \(\{0,1,2,3,4,5,6,7,8,9,0\}\).

Entrenamiento de una máquina de aprendizaje

La construcción de una máquina de aprendizaje requiere encontrar un conjunto de parámetros que definan de manera específica a la función \(f\). El proceso de encontrar tales parámetros se conoce como entrenamiento de la máquina. Es decir el entrenamiento consiste en encontrar (estimar) tal conjunto de parámetros.

Racional conceptual

El entrenamiento de una máquina de aprendizaje es una forma de modelamiento de tipo estadístico. Básicamente el proceso de entrenamiento utiliza un conjunto de datos del espacio de entrada y las etiquetas o valores asociados en el conjunto de salida.

Conjunto de entrenamiento

Al adoptar un enfoque de aprendizaje de máquina el conjunto de dígitos (datos) \(\boldsymbol{x}=\{x_1, \cdots, x_N\}\) utilizado para entrenar la máquina de aprendizaje es llamado un conjunto de entrenamiento.

Tensor objetivo

Las categorías (etiquetas) de los dígitos en el conjunto de entrenamiento se conocen de antemano, generalmente inspeccionándolos individualmente y etiquetándolos manualmente. Podemos expresar la etiqueta de un dígito usando un tensor objetivo \( \boldsymbol{t} \), que representa la identidad del dígito correspondiente.

Codificación one-hot

En el párrafo anterior parece extraño mencionar que en la salida hay un tensor. En realidad, cuando se tienen varias etiquetas no numéricas, es conveniente recodificar las etiquetas usando tensores binarios (con valor cero o uno únicamente).

Esto se hace de la siguiente manera. Si se tiene \(p\) etiquetas, digamos 10 en el caso de los dígitos, entonces las etiquetas se convierten en tensores unidimensionales de tamaño \(p\), en donde todos los elementos son cero excepto en la posición que corresponde a la etiqueta que representa.

La siguiente tabla ilustra la codificación one-hot en el caso de los dígitos.

dígito	one-hot
0	1000000000
1	0100000000
2	0010000000
3	0001000000
4	0000100000
5	0000010000
6	0000001000
7	0000000100
8	0000000010
9	0000000001

Variables categóricas en la entrada

La codificación one-hot es también utilizada cuando se tienen variables categóricas en el espacio de entrada. Esta es la forma como datos categóricos y datos numéricos pueden interactuar. Por ejemplo, si una variable en el espacio de entrada es color, y hay digamos 3 colores: rojo, verde y azul, entonces la codificación one-hot puede ser:

color	one-hot
rojo	100
verde	010
azul	001

En este caso, la variable de entrada color es reemplazada por las tres columnas de la codificación one-hot.

Algoritmo de entrenamiento de una máquina de aprendizaje

Los algoritmos de entrenamiento de máquinas de aprendizaje consisten básicamente en procesos de optimización de una función objetivo, que denominaremos función de pérdida.

Por ejemplo, supongamos que los valores \(y=f(x)\) de la máquina de aprendizaje son números reales. Entonces los datos de entrenamiento son digamos \(\{x_1,\ldots, x_n\}\). Si denotamos \(\{y_1,\ldots,y_n\}\) a las etiquetas (en este caso números reales) asociadas a los datos de entrenamiento, una función de pérdida se puede definir como sigue:

En cada paso del proceso de entrenamiento, la función \(f\) calculada en \(x_i\) entrega un valor digamos \(\tilde{y}_i\). Este valor en principio es diferente de \(y_i\), debido a que justamente estamos entrenando la máquina para que aprenda que \(f(x_i)=y_i\).

Entonces se define por ejemplo:

\[ \mathcal{Loss} = \tfrac{1}{n}\sum_{i=1}^{n}(y_i - \tilde{y}_i)^2. \]

El propósito del algoritmo de entrenamiento es encontrar un conjunto de parámetros para función \(f\), que hace que la función \(\mathcal{Loss}\) tome un valor minimal, siguiendo algunos criterios que se especifican más adelante.

Nota

No necesariamente un algoritmo de aprendizaje encuentra un conjunto de parámetros que minimiza globalmente a la función de pérdida. Esto se debe a que en algunos caso los mínimos globales pueden corresponder a regiones sin capacidad suficiente de generalización.

Capacidad de generalización

La capacidad de una máquina de aprendizaje para etiquetar correctamente nuevos ejemplos (no vistos antes por la máquina) se conoce como capacidad de generalización.

Buscamos máquinas con muy buena capacidad de generalización.

Conjunto de validación

La capacidad de generalización de una máquina de aprendizaje se evalúa con un conjunto de datos de entrada con sus respectivas etiquetas, con la misma estructura de los datos de entrenamiento. Por ejemplo, en el conjunto de datos de entrenamiento usaremos \(70,000\) datos, es decir, \(70,000\) imágenes con sus respectivas etiquetas. Seleccionaremos digamos \(60,000\) para entrenar a la máquina y en consecuencia \(10,000\) para validación.

Seleccionar adecuadamente cada conjunto entrenamiento/validación es crucial para obtener máquinas de aprendizaje que tengan alta capacidad de generalización.

Extracción de características

Para la mayoría de las aplicaciones prácticas, las variables de entrada originales generalmente se preprocesan transformándolas en un nuevo espacio de variables, donde se espera que el reconocimiento de patrones sea más fácil de resolver.

Esta etapa de preprocesamiento es a veces también llamado extracción de características (feature extraction).

Por ejemplo, el valor medio de la intensidad de una imagen sobre una subregión rectangular se puede evaluar de manera extremadamente eficiente y un conjunto de tales funciones pueden resultar muy eficaces en la detección rápida de rostros.

Aprendizaje supervisado

Aplicaciones en las que los datos de entrenamiento comprenden ejemplos de los tensores de entrada junto con sus correspondientes tensores objetivo, se conocen como problemas de aprendizaje supervisado.

Casos como el ejemplo de reconocimiento de dígitos, en el que el objetivo es asignar a cada tensor de entrada una etiqueta, se denominan problemas de clasificación.

Problemas de regresión

Si la salida deseada consta de una o más variables continuas, entonces la tarea se llama regresión.

Aprendizaje no supervisado

En otros problemas de reconocimiento de patrones, los datos de entrenamiento consisten en un conjunto de tensores \(x\) de entrada sin ningún valor objetivo correspondiente. El objetivo en este caso es detectar patrones sin supervisión.

Los problemas de aprendizaje en los que se busca descubrir grupos de ejemplos similares dentro de los datos, se llaman problemas de agrupación (clustering).

Desde el punto de vista estadístico lo que busca es determinar la distribución de datos en el espacio de entrada y el problema se conoce como estimación de densidad.

Aprendizaje reforzado

La técnica del aprendizaje reforzado se refiere al problema de encontrar acciones adecuadas para tomar en una situación dada, para maximizar una recompensa. Aquí, el algoritmo de aprendizaje no recibe ejemplos de resultados óptimos, en contraste con el aprendizaje supervisado, sino que deben descubrirlos por un proceso de prueba y error.

Normalmente hay una secuencia de estados y acciones en las que el algoritmo de aprendizaje está interactuando con su entorno. En muchos casos, la acción actual no solo afecta la recompensa inmediata, sino que también tiene un impacto en la recompensa en todos los pasos de tiempo posteriores.

Por ejemplo, mediante el uso de técnicas apropiadas de aprendizaje reforzado, una red neuronal puede aprender a jugar ajedrez con un alto nivel de destreza.

Aquí la red debe aprender a asumir una posición en el tablero como entrada, junto con el resultado de un movimiento fuerte como salida. Esto se hace haciendo que la red juegue contra una copia de sí misma durante quizás millones de juegos.