Algebra tensorial
Contents
Algebra tensorial#
Introducción#
En esta lección revisamos el las operaciones tensoriales que se utilizan a diario en la inteligencia artificial. Póngale principal atención al producto tensorial general al final de la lección.
El álgebra tensorial es tan importante en la inteligencia artificial que las tecnologías de hardware y las técnicas matemáticas para optimizar el cálculo tensorial son tema de desarrollo e investigación mas recientes. La tecnología como GPU’s, TPU’s y otras mas recientes se orientan casi exclusivamente al álgebra tensorial.
Por ejemplo Nvidia., el gigante tecnológico líder en GPU’s ha desarrollado nuevas técnicas para el cálculo del álgebra tensorial, obviamente orientadas a sus GPU’s que maximizan el rendimiento
Algebra tensorial básica#
NumPy está preparado para trabajar con las operaciones ordinarias del álgebra lineal y de manera más extendida con álgebra tensorial directamente. Los siguientes ejemplos muestran como sumar tensores. Usaremos tensores de tamaño \((3, 2, 3)\) en los ejemplos.
import numpy as np
# Operaciones con Tensores
# Usamos 3*2*3 arrays (tensores)
a = np.array([[[1,2,3],[4,5,6]],[[10,20,30],[40,50,60]],[[100,200,300],[400,500,600]]])
print('tamaño de a = {}\n'.format(a.shape))
print('a =',a)
# Observe que se tiene 3 capas con shape 2*3
tamaño de a = (3, 2, 3)
a = [[[ 1 2 3]
[ 4 5 6]]
[[ 10 20 30]
[ 40 50 60]]
[[100 200 300]
[400 500 600]]]
Multiplicación por una constante: -1*Tensor#
# multiplicar por -1
b = -a
print('tamaño de b = {}\n'.format(b.shape))
print('b =', b)
tamaño de b = (3, 2, 3)
b = [[[ -1 -2 -3]
[ -4 -5 -6]]
[[ -10 -20 -30]
[ -40 -50 -60]]
[[-100 -200 -300]
[-400 -500 -600]]]
Suma de tensores#
Se asume que los tensores que se suman tienen exactamente la misma forma (shape). Puede haber tantos sumando como se quiera. La suma ocurre componente a componente, es decir se suman las componentes que están en la misma posición en cada uno de los tensores.
# suma
c = a + b
print('tamaño de c = {}\n'.format(c.shape))
print('c =', c)
tamaño de c = (3, 2, 3)
c = [[[0 0 0]
[0 0 0]]
[[0 0 0]
[0 0 0]]
[[0 0 0]
[0 0 0]]]
Resta de dos tensores#
Se asume que los tensores que se restan tienen exactamente la misma forma (shape). La resta ocurre componente a componente, es decir se restan las componentes que están en la misma posición en cada uno de los dos tensores.
# diferencia entre dos tensores
c = a - b
print('tamaño de c = {}\n'.format(c.shape))
print('c =', c)
tamaño de c = (3, 2, 3)
c = [[[ 2 4 6]
[ 8 10 12]]
[[ 20 40 60]
[ 80 100 120]]
[[ 200 400 600]
[ 800 1000 1200]]]
Producto de Hadamard#
Se asume que los tensores que se multiplican tienen exactamente la misma forma (shape). La multiplicación ocurre componente a componente, es decir se multiplican las componentes que están en la misma posición en cada uno de los dos tensores.
# producto de Hadamard
c = a * b
print('a =', a)
print()
print('b =', b)
print()
print('tamaño de c = {}\n'.format(c.shape))
print('a * b =', c)
a = [[[ 1 2 3]
[ 4 5 6]]
[[ 10 20 30]
[ 40 50 60]]
[[100 200 300]
[400 500 600]]]
b = [[[ -1 -2 -3]
[ -4 -5 -6]]
[[ -10 -20 -30]
[ -40 -50 -60]]
[[-100 -200 -300]
[-400 -500 -600]]]
tamaño de c = (3, 2, 3)
a * b = [[[ -1 -4 -9]
[ -16 -25 -36]]
[[ -100 -400 -900]
[ -1600 -2500 -3600]]
[[ -10000 -40000 -90000]
[-160000 -250000 -360000]]]
División entre vectores: componente a componente#
Se asume que los tensores que se dividen componente a componente tienen exactamente la misma forma (shape). La división ocurre componente a componente, es decir se dividen entre sí las componentes que están en la misma posición en cada uno de los dos tensores.
# división componente a componente
c = a / b
print("c=",c)
print(c.shape)
c= [[[-1. -1. -1.]
[-1. -1. -1.]]
[[-1. -1. -1.]
[-1. -1. -1.]]
[[-1. -1. -1.]
[-1. -1. -1.]]]
(3, 2, 3)
Producto escalar (dot product)#
Si \(a=(a_1,a_2,a_3)\) y \(b=(b_1,b_2, b_3)\), el el producto escalar entre \(a\) y \(b\) está definido por:
Este producto es base de mucho métodos estadísticos, como la comparación misma de vectores.
Con NumPy escribimos:
# dot product (vectores): c = sum(a_i*b_i)
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.dot(a,b)
print("c = <a, b> =",c)
print("tamaño de c =",c.shape)
c = <a, b> = 32
tamaño de c = ()
Producto de matrices (2D-Tensores)#
Supongamos que \(A=[a_{ij}]_{N\times P}\) y \(B=[b_{jk}]_{P\times Q}\) son matrices de tamaños (shape) \(N\times P\) y \(P\times Q\) respectivamente. Entonces \(C = A\times B\) es una matriz \(C=[c_{ik}]_{N\times Q}\) de tamaño \(P\times Q\), en donde:
Observe detenidamente el cálculo mostrado en la siguiente imagen, el cual ilustra el producto entre dos matrices, cada una de forma \((2, 2)\) .
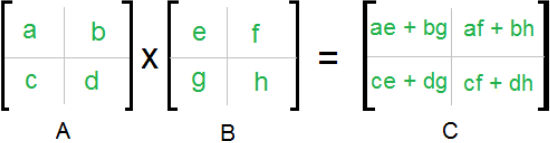
Fuente: studypug.
En Numpy existen varias manera de calcular el producto entre dos matrices. Si \(A\) y \(B\) son dos matrices, entonces el producto matricial se denota en una de las siguiente formas
C = A @ B
C = np.matmul(A,B)
C = np.dot(A,B)
La última expresión es bastante sugerente. Indica que el producto punto se define entre matrices, y el caso que estudiamos previamente es el caso particular en donde los tensores tiene forma \((1, n)\) y \((n, 1)\) respectivamente.
Más adelante vamos a constatar que el producto entre matrices es un caso particular del producto tensorial general.
# producto de matrices (tensores ): c = sum(a_i*b_i)
A = np.array([[1,2,3],[4,5,6]])
B = np.array([[10,20,30,40],[50,60,70,80],[90,100,110,120]])
print("A =",A)
print("A.shape =",A.shape)
print()
print("B =",B)
print("B.shape =",B.shape)
print()
# producto de matrices ( resultado equivalente)
# se prefiere el cálculo de C o D
C = A @ B
D = np.matmul(A,B)
E = np.dot(A,B)
print("C=",C)
print("C.shape =",C.shape)
print("D=",D)
print("E=",E)
A = [[1 2 3]
[4 5 6]]
A.shape = (2, 3)
B = [[ 10 20 30 40]
[ 50 60 70 80]
[ 90 100 110 120]]
B.shape = (3, 4)
C= [[ 380 440 500 560]
[ 830 980 1130 1280]]
C.shape = (2, 4)
D= [[ 380 440 500 560]
[ 830 980 1130 1280]]
E= [[ 380 440 500 560]
[ 830 980 1130 1280]]
El producto matricial puede ser concatenado en Numpy#
Pueden escribirse varias expresiones de producto punto seguidas. Si no hay paréntesis en al expresión, el cálculo ocurre de izquierda a derecha. Veamos el siguiente ejemplo. Ejecútelo usted mismo y obtenga sus propias conclusiones.
# a.dot puede ser encadenado con arreglos 2D
a = np.eye(2) #matriz identidad 2x2
print('a =\n', a)
print()
b = np.ones((2,2))*2 # matriz 2x2, lleno con números 2 .
print ('b =\n ', b)
print()
print('a.dot(b)\n =', a.dot(b))
print()
print('a.dot(b).dot(b) =\n', a.dot(b).dot(b) )
a =
[[1. 0.]
[0. 1.]]
b =
[[2. 2.]
[2. 2.]]
a.dot(b)
= [[2. 2.]
[2. 2.]]
a.dot(b).dot(b) =
[[8. 8.]
[8. 8.]]
Resumen de producto entre tensores simples#
La imagen resume la manera como se realizan los distintos tipo de producto tensorial revisado hasta este momento.
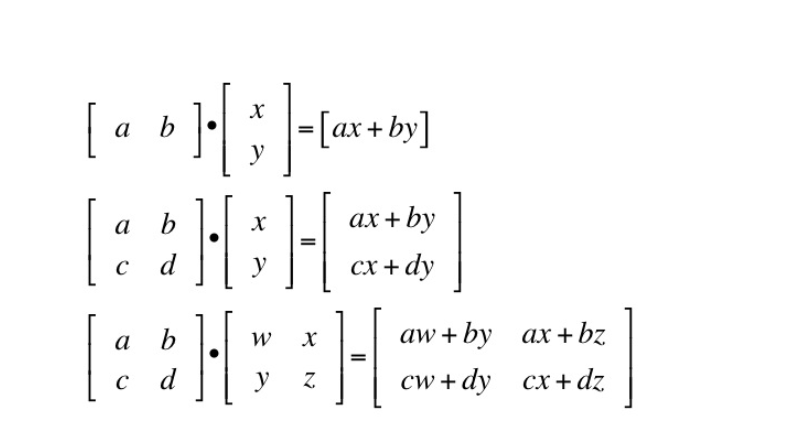
Fuente wordpress
Producto tensorial general#
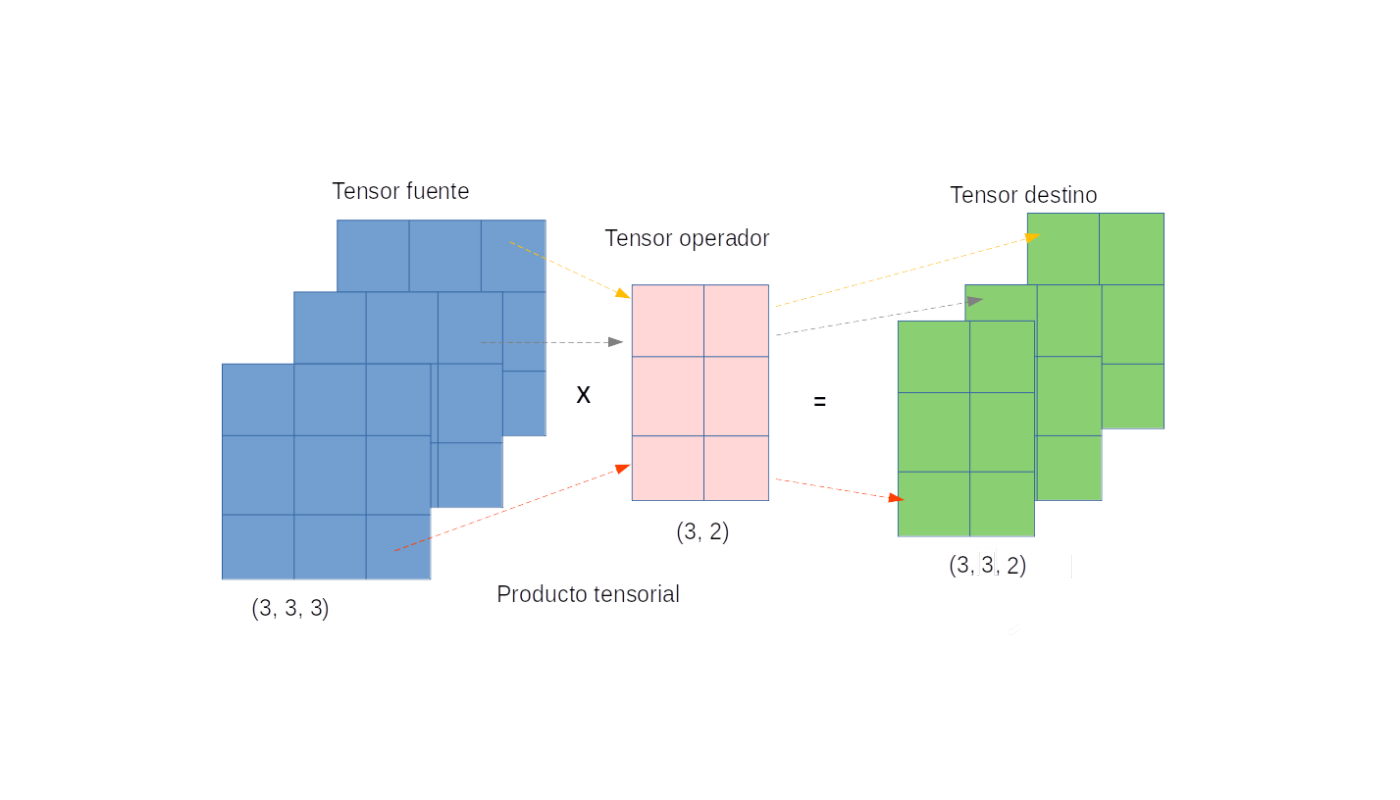
Fuente: Alvaro Montenegro
La imagen ilustra la operación tensorial mas usual en inteligencia artificial. El tensor de la izquierda (azul) tiene forma \((3,3,3)\). Puede imaginar que este tensor representa una imagen a color de tamaño \(3\times 3\). El tensor en el centro tiene forma \((3, 2)\) (rosa), el cual puede usted pensar como un filtro (más preciso sería decir un kernel) qu va a operar sobre cada una de las capas de color de la imagen. ¿Y cómo lo hace?
Pues sencillamente efectúa el producto de la matriz de cada color, es decir cada capa de la matriz azul con el filtro, es decir con la matriz rosa.
Entonces el producto se efectúa de la siguiente manera:
La primera capa de la matriz azul tiene forma \((3,3)\) se multiplica matricialmente con la matriz rosa, dando como resultado la matriz de la primera capa del tensor destino (turquesa), de forma \((3, 2)\).
La segunda capa de la matriz azul tiene forma \((3,3)\) se multiplica matricialmente con la matriz rosa, dando como resultado la matriz de la segunda capa del tensor destino (turquesa), de forma \((3, 2)\).
La tercera capa de la matriz azul tiene forma \((3,3)\) se multiplica matricialmente con la matriz rosa, dando como resultado la matriz de la tercera capa del tensor destino (*verde), de forma \((3, 2)\).
Al final el tensor verde tiene forma \((3, 3, 2)\).
De manera un poco mas general, vamos a suponer que cada elemento en los tensores de dimensión 3 se indexan mediante coordenadas (fila, columna, profundidad) y que los tensores de dimensión 2 se indexan como (fila, columna).
La siguiente imagen ilustra la forma de un producto tensorial.
A la izquierda (azul) se tiene un tensor de tamaño digamos \(n \times p \times s\).
El tensor que está operando en el centro (rosa) es de tamaño \(p \times r\). Este actúa operando en este caso sobre cada capa del tensor de la izquierda haciendo un producto usual de matrices.
Por lo que el tensor resultante (verde) a la derecha tiene tamaño \(n \times r \times s\)
Explicación del producto con un ejemplo parcial#
La explicación del proceso es la siguiente:
Cada capa frontal del tensor azul es multiplica por el tensor rosa y el resultado es colocando como una capa frontal en el tensor resultante (verde).
Cada multiplicación es entre dos matrices (azul * rosa) y el resultado es una matriz (verde).
Cada multiplicación de matrices se hace por la fórmula fila (matriz azul) * columna (matriz rosa)
Supongamos por ejemplo que una capa es \( azul = \begin{pmatrix} 1 & 2 & 1\\ 3 & 4 & 1 \\ 4 & 5 & 0\\ \end{pmatrix}\), \(rosa = \begin{pmatrix} 5 & 10\\ 20 & 30 \\ 4 & 1\end{pmatrix}\)
Entonces se tiene que
Para terminar la lección, revisemos el siguiente ejemplo numérico
import numpy as np
a = np.array([[[1,2],
[3,4],
[5,6]],
[[7,8],
[9,10],
[11,12]],
[[13,14],
[15,16],
[17,18]],
[[19,20],
[21,22],
[23,24]]])
b = np.array([[10],[100]])
c = a.dot(b)
d = a@b
# revisamos este subcálculo. a_0 es la primera matriz 3x2 del arreglo A.
a_0 = a[0,:,:]
# e es la primera matriz de tamaño 3*1 del producto. Compare los resultados.
e = a_0@b
print('a.shape =',a.shape)
print('a =\n', a)
print()
print('b.shape =',b.shape)
print(' b=\n', b)
print()
print('c.shape =',c.shape)
print('c =\n', c)
print()
print('d.shape =',d.shape)
print('d =\n', d)
print()
print('e.shape =\n',e.shape)
print('e=', e)
print()
print('a_0.shape',a_0.shape)
print('a_0 =\n', a_0)
a.shape = (4, 3, 2)
a =
[[[ 1 2]
[ 3 4]
[ 5 6]]
[[ 7 8]
[ 9 10]
[11 12]]
[[13 14]
[15 16]
[17 18]]
[[19 20]
[21 22]
[23 24]]]
b.shape = (2, 1)
b=
[[ 10]
[100]]
c.shape = (4, 3, 1)
c =
[[[ 210]
[ 430]
[ 650]]
[[ 870]
[1090]
[1310]]
[[1530]
[1750]
[1970]]
[[2190]
[2410]
[2630]]]
d.shape = (4, 3, 1)
d =
[[[ 210]
[ 430]
[ 650]]
[[ 870]
[1090]
[1310]]
[[1530]
[1750]
[1970]]
[[2190]
[2410]
[2630]]]
e.shape =
(3, 1)
e= [[210]
[430]
[650]]
a_0.shape (3, 2)
a_0 =
[[1 2]
[3 4]
[5 6]]
Ejercicios#
Con estos ejercicios hacemos una generalización adicional del producto tensorial.
Cree con Numpy un tensor a aleatorio de forma \((3, 4, 5)\).
Cree con Numpy un tensor b aleatorio de forma \((5, 2)\).
Calcule el producto \(c = a.dot(b)\)
Escriba el resultado.
Calcule la forma del tensor c.
Explique como se ha hecho el producto.
Cambie la forma de los tensores arbitrariamente y reintente el cálculo.
Explique lo ocurrido.
Cree con Numpy un tensor a aleatorio de forma \((3, 4, 5)\).
Cree con Numpy un tensor b aleatorio de forma \((2, 5, 3)\).
Calcule el producto \(c = a.dot(b)\)
Escriba el resultado.
Calcule la forma del tensor c.
Explique como se ha hecho el producto.
Cambie la forma de los tensores arbitrariamente y reintente el cálculo.
Explique lo ocurrido.


