Diferenciación automática con torch.autograd
Contents
Diferenciación automática con torch.autograd#
Introducción#
Al entrenar redes neuronales, el algoritmo más utilizado es la propagación hacia atrás (back propagation). En este algoritmo, los parámetros (pesos del modelo) se ajustan de acuerdo con el gradiente de la función de pérdida con respecto al parámetro dado.
Para calcular esos gradientes, PyTorch tiene un motor de diferenciación incorporado llamado torch.autograd. Admite el cálculo automático del gradiente para cualquier gráfo computacional.
Tensores, funciones y grafo computacional#
Considere la red neuronal de una capa más simple, con entrada \(x\), parámetros \(w\) y \(b\), y alguna función de pérdida. Se puede definir en PyTorch de la siguiente manera:
import torch
x = torch.ones(5) # entrada
y = torch.Tensor([0, 1, 0]) # etiqueta (valor verdadero)
w = torch.randn(5,3, requires_grad=True) # matriz de pesos
b = torch.randn(3, requires_grad=True)# bias
z = torch.matmul(x,w)+b # calculo de la capa
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)
print('x= ', x)
print('y= ',y)
print('w= ', w)
print('b= ', b)
print('z= ', z)
print('loss= ', loss)
x= tensor([1., 1., 1., 1., 1.])
y= tensor([0., 1., 0.])
w= tensor([[-1.5900, 0.4014, -1.3991],
[ 0.7548, 1.2660, 0.8778],
[ 0.1134, -0.7176, 0.4875],
[ 0.0147, -0.2765, 1.1915],
[-0.9523, -1.1692, 0.4101]], requires_grad=True)
b= tensor([-0.8247, 0.6761, -0.7123], requires_grad=True)
z= tensor([-2.4841, 0.1801, 0.8555], grad_fn=<AddBackward0>)
loss= tensor(0.6323, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
Entropía Cruzada#
Recuerde que si \(p=(p_1, p_2, p_3)\) y \(q=(q_1, q_2, q_3)\) son dos distribuciones de probabilidad, de las cuales una se supone la verdadera, digamos \(q\) y la otra una aproximación, en este caso \(p\)., entonces la entropía cruzada entre \(p\) y \(q\) se define mediante
La entropía cruzada mide que tanto se parece la disribución \(p\) a la distribución \(q\). En el ejemplo se tiene que \(p = \text{softmax(z)}\) y además \(q=y\). Observe que por ejemplo \(z_1 = x^T w_1\), en donde \(w_1\) es la columna 1 de \(w\). Note que además \(p\) es función de los parámetros \(w\) y \(b\).
Este código define el siguiente grafo computacional:
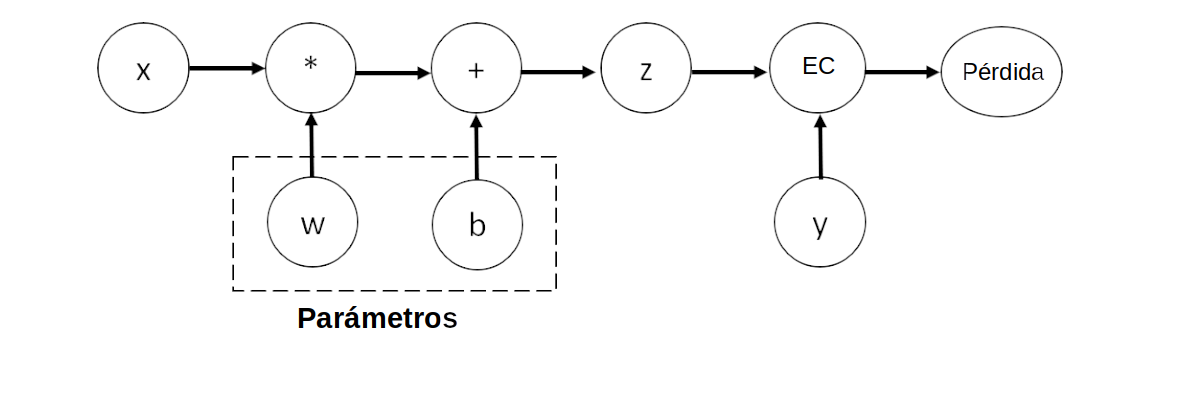
Grafo computacional del cálculo descrito arriba.
La propiedad requires_grad indica que son variables con respecto a las cuales se desea calcular el gradiente de la función loss.
No es necesario declararlas como tal desde el comienzo. Puede hacerlo luego mediante el método
x.requires_grad(True).
Una función aplicada a tensores de un objeto de la clase Function, la cual viene equipada con lo necesario para la diferenciación automática. Una referencia a la función gradiente (back propagation) se almacena en grad_fn. Por ejemplo:
print('Gradient function for z =', z.grad_fn)
print('Gradient function for loss =', loss.grad_fn)
Gradient function for z = <AddBackward0 object at 0x7fbf7001df10>
Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x7fbf7001da90>
Cálculo de gradientes#
Vamos a calcular \(\frac{\partial loss} {\partial w}\) y \(\frac{\partial loss} {\partial b}\).
loss.backward()
print('w.grad= ', w.grad)
print('b.grad= ', b.grad)
w.grad= tensor([[ 0.0257, -0.1517, 0.2339],
[ 0.0257, -0.1517, 0.2339],
[ 0.0257, -0.1517, 0.2339],
[ 0.0257, -0.1517, 0.2339],
[ 0.0257, -0.1517, 0.2339]])
b.grad= tensor([ 0.0257, -0.1517, 0.2339])
Admonition
Nota
Solo podemos obtener las propiedades grad para los nodos hoja del grafo computacional, que tienen la propiedad require_grad establecida en True. Para todos los demás nodos de nuestro gráfico, los degradados no estarán disponibles.
Solo podemos realizar cálculos de gradiente usando hacia atrás una vez en un gráfico dado, por razones de rendimiento. Si necesitamos hacer varias llamadas hacia atrás en el mismo gráfico, debemos pasar retain_graph = True a la llamada hacia atrás.
Deshabilitar el seguimiento de gradientes#
De forma predeterminada, para todos los tensores con require_grad = True se está rastreando su historial computacional y admiten el cálculo del gradiente. Sin embargo, hay algunos casos en los que no necesitamos hacer eso, por ejemplo, cuando hemos entrenado el modelo y solo queremos aplicarlo a algunos datos de entrada, es decir, solo queremos hacer cálculos reenviados a través de la red. Podemos detener el seguimiento de los cálculos rodeando nuestro código de cálculo con el bloque torch.no_grad ():
z = torch.matmul(x,w)+b
print(z.requires_grad)
with torch.no_grad():
z = torch.matmul(x,w)+b
print(z.requires_grad)
True
False
Alternativamente se puede usar el método detach:
z = torch.matmul(x,w)+b
z_det = z.detach()
print(z_det.requires_grad)
False
Existen motivos por los que quizás desee deshabilitar el seguimiento de gradientes:
Para marcar algunos parámetros en su red neuronal como parámetros congelados. Este es un escenario muy común para ajustar una red previamente entrenada (finetunning)
Para acelerar los cálculos cuando solo está haciendo un paso hacia adelante, porque los cálculos en tensores que no siguen los gradientes serían más eficientes.
Más sobre grafos computacionales#
Conceptualmente, autograd mantiene un registro de datos (tensores) y todas las operaciones ejecutadas (junto con los nuevos tensores resultantes) en un gráfico acíclico dirigido (DAG) que consta de objetos de tipo Function. En este DAG, las hojas son los tensores de entrada, las raíces son los tensores de salida. Al trazar este gráfico desde las raíces hasta las hojas, puede calcular automáticamente los gradientes usando la regla de la cadena.
En un paso hacia adelante (foreward), autograd hace dos cosas simultáneamente:
ejecuta la operación solicitada para calcular un tensor resultante
mantiene la función de gradiente de la operación en el DAG.
El paso hacia atrás(backward) comienza cuando se llama a .backward() en la raíz del DAG. autograd entonces:
calcula los gradientes de cada
.grad_fn,los acumula en el atributo
.graddel tensor respectivoutilizando la regla de la cadena, se propaga hasta los tensores de las hojas.
Nota
Los DAG son dinámicos en PyTorch. Una cosa importante a tener en cuenta es que el gráfico se recrea desde cero; después de cada llamada .backward (), autograd comienza a completar un nuevo grafo. Esto es exactamente lo que le permite utilizar declaraciones de flujo de control en su modelo; puede cambiar la forma, el tamaño y las operaciones en cada iteración si es necesario.


